高二数学解三角形单元测试

高二数学解三角形单元测试   ( 命题　方锦昌)

班级_________　　姓名_______　　　学号__________

一、选择题:

1、已知△ABC中，a＝4，b＝4 ，∠A＝30°，则∠B等于 (　　 )
　　A．30°　　 B．30°或150°　　　C．60°　　　D．60°或120°
2、已知△ABC中，AB＝6，∠A＝30°，∠B＝120°，则△ABC的面积( 　)
　　A．9　　　　B．18　　　 　C．9 　　　 D．18

3、在△ABC中，根据下列条件解三角形，其中有一解的是 (　　)

A．b＝7，c＝3，C＝30°　　　　　 　B．b＝5，c＝4 ，B＝45°　

C．a＝6，b＝6 ，B＝60°　　　　　D．a＝20，b＝30，A＝30°

4、在△ABC中，已知三边a、b、c满足(a＋b＋c)(a＋b－c)＝3ab，则∠C等于 ( 　)

A．15°　　　 　B．30°　　　　　 　 C．45°　　　　　 D．60°
5、已知在△ABC中:，sinA: sinB: sinC＝3: 5 :7，那么这个三角形的最大角是 (　　)　A．135°　　 　B．90°　　　C．120°　　　　 D．150°

6、海上有A、B两个小岛相距10海里，从A岛望C岛和B岛成60°的视角，从B岛望C岛和A岛成75°的视角，则B、C间的距离是 (　　)
　A.10 海里　　　　  　B.5海里　　 　C. 5 海里　　　　D.5 海里

7．在△ABC中，A为锐角，lgb+lg()=lgsinA=－lg, 则△ABC为　 （　 ）

A. 等腰三角形　　B. 等边三角形　 　 C. 直角三角形　 　　D. 等腰直角三角形

8．在三角形ABC中,已知A,b=1,其面积为,则为　　(　)   A.　　　　  B. 　　　　 C. 　　　 D.

9．在△ABC中，若，则△ABC的形状是（ 　 ）

A．直角三角形  　B．等腰或直角三角形 　 C．等腰三角形　 　D．不能确定

10.　已知锐角三角形三边分别为3，4，a，则a的取值范围为（ 　 ）

A．　　　 B．　　　　C．　　　 D．

二、填空题：

11、在△ABC中，cosA＝,sinB＝,则cosC的值为______

12、在△ABC中，若sinAsinB＝cos²，则△ABC为_____ _.

13、某舰艇在A处测得遇险渔船在北偏东45°距离为10海里的C处，此时得知，该渔船沿北偏东105°方向，以每小时9海里的速度向一小岛靠近，舰艇时速21海里，则舰艇到达渔船的最短时间是_________________
14．在△ABC中，若∶∶∶∶，则______  

15. （1）在中，若，，且三角形有解，则的取值范围为　　　 

（2）2002年在北京召开的国际数学家大会，会标是以我国古代数学家赵爽的弦图为基础设计的．弦图是由四个全等直角三角形与一个小正方形拼成的一个大正方形（如图）．如果小正方形的面积为1，大正方形的面积为25，直角三角形中较小的锐角为，那么的值等于　　　　　　　　　　　　　　　　　 ．

三、解答题：

16 (本小题共14分)在ABC中，设，求A的值。

 

 17、在△ABC中，a、b是方程x²－2x＋2＝0的两根，且2cos(A＋B)＝－1.

(1)、求角C的度数；　　（2）、求c;　　　 （3）、求△ABC的面积.

 

18、我炮兵阵地位于地面A处，两观察所分别位于地面点C和D处，已知CD=6000m ，　

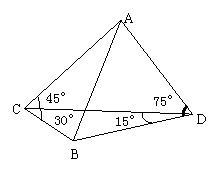∠ACD=45°,∠ADC=75°, 目标出现于地面点B处时，测得∠BCD=30°∠BDC=15°(如图）求：炮兵阵地到目标的距离.

 

19． 如图，已知的半径为1，点C在直径AB的延长线上，BC＝1，点P是上半圆上的一个动点，以PC为边作正三角形PCD，且点D与圆心分别在PC两侧.

（1）若，试将四边形OPDC的面积y表示成的函数；

（2）求四边形OPDC面积的最大值.

20、（2006·江西·19题·12分）在锐角三角形△ABC中，角A，B，C的对边分别为a,b,c,已知sinA=，①求tan²()+sin²()的值；②若a=2,S_△ABC=，求b的值。

21．（1）某海上缉私小分队驾驶缉私艇以的速度从处出发沿北偏东的方向航行，进行海面巡逻，当行驶半小时到达处，发现在北偏西的方向上有一艘船，船位于处北偏东的方向上，求缉私艇与船的距离。

 

2）已知顶点的直角坐标分别为，，．（1）若，求的值；（2）若是钝角，求的取值范围．

 

参考答案:

一、选择题:

1、　 A　；2、 　C　； 3、 　C　； 4、  D　；5、  C ； 6、  C　；

7．　D ； 8．　B ； 9．　 B　； 10.　　C　

二、填空题：

11、 ； 12、 等腰三角形； 13、40分钟；14． 120度；

15.　； （2）

三、解答题：

16解：根据正弦定理

　

 17、解：(1)∵2cos(A＋B)＝-1，∴cosC＝.∴角C的度数为60°.

(2)∵a、b是方程x²－2x＋2＝0的两根，∴a＋b＝2，ab＝2,

c²＝a²＋b²－2abcosC＝(a＋b)²－2ab(cosC＋1)＝12－2＝10.∴c＝.

(3)S＝absinC＝.

18、解：在△ACD中，

　　　 根据正弦定理有:

　　　 同理：在△BCD中，

　　　　　　　　　　　　  ，

 根据正弦定理有：　在△ABD中，　根据勾股定理有：

所以：炮兵阵地到目标的距离为。

19．解：设且在中，，，由余弦定理得： ，所以　 因为，，所以当即，也即时，有最大值且为故当时，使四边形的面积最大。

20、解：（1）因为锐角△ABC中，A＋B＋C＝p，，所以cosA＝，则

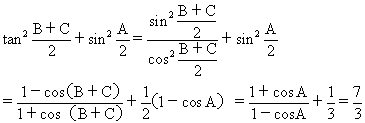
（2），则bc＝3。将a＝2，cosA＝，c＝代入余弦定理：中得解得b＝

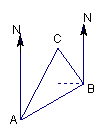
21．（1）解：如图，由题意，，

所以，由正弦定理：

即

故缉私艇与船的距离为

（2）解析： （1），，若c=5， 则，∴，∴sin∠A＝；

2）若∠A为钝角，则解得，∴c的取值范围是；