高二数学（理）第二学期期末联考模拟试卷

高二数学（理）第二学期期末联考模拟试卷

参考公式：

1、相关性检验的临界值表：

	0.50	0.40	0.25	0.15	0.10	0.05	0.025	0.010	0.005	0.001
	0.455	0.708	1.323	2.072	2.706	3.841	5.024	6.635	7.879	10.828

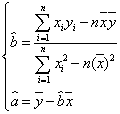
2、的计算公式：　　　　　　　　　，

3、卡方值计算公式：.

一、填空题：本大题共14小题,每小题5分，共计70分．不需写出解答过程,请把答案直接填写在答题卡相应位置上.

1、=　　　　　　　  

2、曲线在处的切线方程是　　　　　　　  

3、若用反证法证明“若，则”，假设内容应是　　　　　　　　　  

4、对于函数，当增加时，增加了　　　　　　 　 

5、若复数和对应的点分别为和，则向量对应的复数为　　　　　　  

6、函数在区间上的最大值和最小值是　　　　　　  

7、为确保信息安全，信息需加密传输，发送方由明文密文（加密），接受方由密文

明文（解密），已知加密规则为：明文对应密文.

例如明文对应加密文，当接受方收到密文时，则解密

得明文为　　　　　 

8、将个正数填入方格中，使每行、每列、

每条对角线上的数的和相等，这个正方形就叫阶幻方.

记为阶幻方对角线的和，如图就是一个3阶幻方，

可知，那么=　　　

9、质点的运动方程是的单位为的单位为，

　　则质点在时的瞬时速度为　　　　　　  .

10、若，则的值为　　　　　　 .

11、平面几何中有结论“周长一定的所有矩形中，正方形的面积最大”，类比到空间可得

　 的结论是　　　　　　　　　　　　　　　　　　　　　　　　　  .

12、实验测得五组的值是线性相关的，则与之间

　 的线性回归方程是　　　　　　　　　　　　　　　　　　　 .

13、已知数列的通项公式，记，

　 通过计算的值，推测出　　　　　　　　.

14、(1＋)⁶(1＋)¹⁰展开式中的常数项为　　　　　　　  .

二、解答题：本大题共6小题，共计90分．请在答题卡指定区域内作答，解答时应写出字说明、证明过程或演算步骤．

15、（本题14分）

　（1）求函数的导数；

　（2）已知函数在和处有极值，求实数的值.

16、（本题14分）

已知复数，当实数取什么值时，复数是：

（1）虚数；（2）纯虚数；（3）复平面内第二、四象限角平分线上的点对应的复数.

17、（本题14分）

　　  考取驾照是一个非常严格的过程，有的人并不能够一次性通过，需要补考.现在有一张某驾校学员第一次考试结果汇总表，由于保管不善，只残留了如下数据（见下表）：

　　

成绩 性别	合　　格	不 合 格	合　 计
男　 性	45	10
女　 性	30
合　 计			105

　 （1）完成此表；

　 （2）根据此表判断：是否可以认为性别与考试是否合格有关？如果可以，请问有多大

　　　　把握；如果不可以，试说明理由.

18、（本题16分）

从5名女生和2名男生中任选3人参加英语演讲比赛，设随机变量表示所选3

人中男生的人数.

（1）求的分布列；　

（2）求的数学期望；

（3）求“所选3人中男生人数”的概率.

19、（本题16分）

已知曲线C₁：（为参数），曲线C₂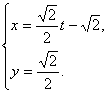：（t为参数）.

（Ⅰ）指出C₁，C₂各是什么曲线，并说明C₁与C₂公共点的个数；

（Ⅱ）若把C₁，C₂上各点的纵坐标都压缩为原来的一半，分别得到曲线C.写出C的参数方程. C公共点的个数和C公共点的个数是否相同？说明你的理由.

20、（本题16分）

已知且，．

（1）求函数的表达式；

（2）已知数列的项满足，试求；

（3）猜想的通项，并用数学归纳法证明．

江苏省泰州市2007～2008年度第二学期期末联考模拟试卷

参考答案

1、　 2、　 3、或　 4、　 5、　6、5，  7、　 8、34　　9、　 10、　11、表面积一定的长方体中，正方体体积最大　　　　 12、13、　　14、4246

15、解：（1）；

　 （2），∵，

　　　 ∴.

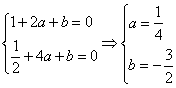16、解：（1）当时，为实数；

　　　 （2）由题意得，当时，是纯虚数；

　　　 （3）由题意得，解之得或.

17、解：（1）

成绩 性别	合　　格	不 合 格	合　 计
男　 性	45	10	55
女　 性	30	20	50
合　 计	75	30	105

　　  （2）假设：性别与考试是否合格无关，

　　　　　 .

　　　　若成立，，∵，

　　　  ∴有97.5%的把握认为性别与考试是否合格有关.

18、解：（1），

　　 （2）；　　　（3）.

19、【试题解析】：(I ) C₁是圆 ，C₂是直线，

C₁的普通方程是，C₂的普通方程是.

因为圆心C₁到直线的距离是1,

所以C₁与C₂只有一个公共点.

(2) 压缩后的参数方程分别为

C₁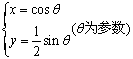：，曲线C₂：.

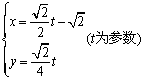化为普通方程为:,: .

联立消元得,

其判别式,

所以压缩后的直线与椭圆仍然只有一个公共点,和C₁与C₂的公共点的个数相同.

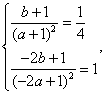20解:(1)由题意得:即解之得:

所以.

(2); ;

;

.

(1)　　 猜想:

证明:①当时, 所以等式成立

②假设且时,等式成立.即.

则当时,

所以,对一切正整数,有