高二数学选修2-1期末考试卷3

高二数学选修2-1期末考试卷3（）

一、选择题（每小题5 分，共10小题，满分50分）

1、对抛物线，下列描述正确的是

　　　 A、开口向上，焦点为　　　　　　　B、开口向上，焦点为

　　　 C、开口向右，焦点为　　　　　　　D、开口向右，焦点为

2、已知A和B是两个命题，如果A是B的充分条件，那么是的　

A、充分条件　　B、必要条件　　 C、充要条件　　D、既不充分也不必要条件

3、椭圆的一个焦点是，那么实数的值为

　　　 A、　　　　　　　 B、　　　　　　　　 C、　　　　　D、

4、在平行六面体ABCD-A₁B₁C₁D₁中，M为AC与BD的交点，若, ，，则下列向量中与相等的向量是　　　　　　　　　　　　　　　   

　　 A、　　B、 　　 C、 　　D、

5、空间直角坐标系中，O为坐标原点，已知两点A（3，1，0），B（-1，3，0），若点C满足=α+β，其中α，βR，α+β=1，则点C的轨迹为　　　　　　　　　　

A、平面　　　　　　　  B、直线　　　　　　  C、圆　　　　　　　　 D、线段

6、已知=(1,2,3), =（3，0，-1），=给出下列等式：

①∣∣=∣∣　② = ③=

 ④ =

其中正确的个数是　　　　　　　　　　　　　　　　　　　　　　　　　　　

A、1个　　　　　　　B、2个　　　　　 C、3个　　　　　  D、4个

7、设，则方程不能表示的曲线为

　　　 A、椭圆　　　　　　　　B、双曲线　　　　　　C、抛物线　　　　　　D、圆

8、已知条件p：<2，条件q：-5x-6<0，则p是q的　　　　　　　　

A、充分必要条件　　　　　  　　　　 B、充分不必要条件

C、必要不充分条件　　　　　　　　　 D、既不充分又不必要条件

9、已知函数f(x)=，若，则k的取值范围是　

A、0≤k<　　　　B、0<k< 　　　 C、k<0或k>　　　　 D、0<k≤

10、下列说法中错误的个数为　　　　　　　　　　　　　　　　　　　　　　 

①一个命题的逆命题为真，它的否命题也一定为真；②若一个命题的否命题为假，则它本身一定为真；③是的充要条件；④与是等价的；⑤“”是“”成立的充分条件.

  A、2　　　　B、3　　　　 C、4　　　 D、5

二、填空题（每小题6分，共6小题，满分36分）

11、已知,(两两互相垂直)，那么=　　　　 。

12、以为中点的抛物线的弦所在直线方程为：　　　　　　　　  ．

13、在△中，边长为，、边上的中线长之和等于．若以边中点为原点，边所在直线为轴建立直角坐标系，则△的重心的轨迹方程为：　　　　　　　　　  ．

14、已知M₁（2，5，-3），M₂（3，-2，-5），设在线段M₁M₂的一点M满足=，则向量的坐标为　　　　 。

15、下列命题

①命题“事件A与B互斥”是“事件A与B对立”的必要不充分条件.

② “am²<bm²”是“a<b”的充分必要条件.

③ “矩形的两条对角线相等”的否命题为假.

④在中，“”是三个角成等差数列的充要条件.

⑤中,若,则为直角三角形.

判断错误的有___________

16、在直三棱柱中，．有下列条件：

①；②；③．其中能成为

的充要条件的是（填上该条件的序号）________．

　　　　　　　

三、解答题（共五小题，满分74分）

17、（本题满分14分）求ax²+2x+1=0（a≠0）至少有一负根的充要条件．

18、（本题满分15分）已知命题p：不等式x－1>m－1的解集为R，命题q：f(x)=－(5－2m)^x是减函数，若p或q为真命题，p且q为假命题，求实数m的取值范围.

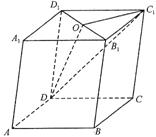
19、（本题满分15分）如图，在平行六面体ABCD-A₁BC₁D₁中，O是

B₁D₁的中点，求证：B₁C∥面ODC₁。

20、（本题满分15分）直线：与双曲线：相交于不同的、两点．

　　　 （1）求AB的长度；

　　　 （2）是否存在实数，使得以线段为直径的圆经过坐标第原点？若存在，求出的值；若不存在，写出理由．

21、（本题满分15分）如图，直三棱柱ABC-A₁B₁C₁底面△ABC中，CA=CB=1，

∠BCA=90°，棱AA₁=2M，N分别是A₁B₁，A₁A的中点。

  （1）求的长度；

  （2）求cos（，）的值；

  （3）求证：A₁B⊥C₁M。

参考答案

一、选择题（每小题5 分，共10小题，满分50分）

1、B　2、C　3、D　4、A　5、B　6、D　7、C　8、B　9、A　10、C

二、填空题（每小题6分，共6小题，满分36分）

11、- 65　12、　13、（） 14、　15、②⑤

16、①、③

三、解答题（共六小题，满分74分）

17、（本题满分14分）解:若方程有一正根和一负根，等价于 a＜0　　　

若方程有两负根，等价于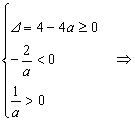0＜a≤1

综上可知，原方程至少有一负根的必要条件是a＜0或0＜a≤1

由以上推理的可逆性，知当a＜0时方程有异号两根；当0＜a≤1时，方程有两负根.

故a＜0或0＜a≤1是方程ax²+2x+1=0至少有一负根的充分条件.

所以ax²+2x+1=0（a≠0）至少有一负根的充要条件是a＜0或0＜a≤1

18、（本题满分15分）解：不等式x－1<m－1的解集为R，须m－1<0

即p是真 命题，m<1

f(x)=－(5－2m)^x是减函数，须5－2m>1即q是真命题，m<2

由于p或q为真命题，p且q为假命题　　

故p、q中一个真，另一个为假命题　因此，1≤m<2

　　　　　　　　　　　　　　　　　　　　　　  　　　　　　　　　　　 

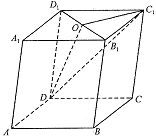
19、（本题满分15分）

证明：设，则

∵∴

∴

∵

∴

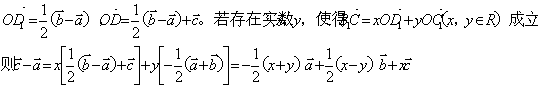
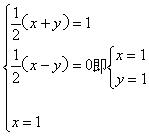
20、（本题满分15分）

联立方程组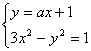消去y得，因为有两个交点，所以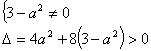，解得。

(1) 。

(2)由题意得  

整 理得

21、（本题满分15分）如图，

解：以为原点，分别为轴，轴，轴建立空间直角坐标系。

（1）　　　 依题意得出；

（2）　　　 依题意得出

∴﹤﹥=

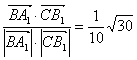
（3）　　　 证明：依题意将