高中二年级数学上册第二次阶段考试试卷（高二上期）
说明：满分100分，考试时间：90分钟。
| 题号 | 一 | 二 | 三 | 总分 | ||||
| 15 | 16 | 17 | 18 | 19 | ||||
| 得分 | ||||||||
一、选择题（本大题共10小题，每小题4分，共40分．）
1. 若直线经过点
，并且与x轴垂直，则该直线的方程是( )
A．
B．
C．
D． 
2. 直线
的倾斜角是( )
A．－30° B． －60° C．120° D．150°
3. 不等式
的解集是( )
A．
B
C． 
D． 
4. 以原点为圆心，且截直线3x＋4y＋15=0所得弦长为8的圆的方程是（ ）
A．
B．
C．
D．
5. 若
，
，则
，2
，
，
中最大一个是（ ）
A． B． C． D．
6. 满足条件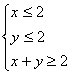
的
的取值范围是（ ）
A．[2,6] B．[2,5] C．[3,6] D．[3,5]
7. 已知
的顶点B、C在椭圆
上，顶点A是椭圆的一个焦点，且椭圆的另一个焦点在BC边上，则的周长是（ ）
A．
B．6 C．
D．12
8. 下列四个命题中的真命题是 （ ）
A.经过定点
，
的直线都可以用方程
表示
B.经过任意两个不同点
，
、
，
的直线都可以用方程
表示
C.不经过原点的直线都可以用方程
表示
D.经过定点
，
的直线都可以用方程
表示
9. 已知点
在圆
上，点
关于直线
的对称点也在圆
上，则实数
、
的值为 （
）
A．
B．
C． 
D．
10．设点
，
若直线
与线段
有交点，则的取值范围是（ ）
A．
B．
C．
D．
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
二、填空题（本大题共4小题，每小题4分，共16分）
11.．直线x – 2y +2 = 0与直线3x – y + 7 = 0的夹角等于____________
12. 已知直线
与
平行，则
___________
13．与椭圆
有相同的焦点且过点(-4,0)的椭圆方程为
14．已知直线
经过点A（1，9），则
的最小值是
三、解答题（本大题共5小题，共44分．解答应写出文字说明，证明过程或演算步骤．）
15. 一直线过点A
，且在两坐标轴上的截距之和为12，求此直线方程。（8分）
解：依题意可知，该直线在
轴，
轴上的截距都不为0，所以可设所求直线方程为，因为直线在两坐标轴上的截距之和为12，
3分
又因为直线过点
，
，
解方程组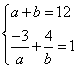
得
， 6分
，
化为一般式得
或
。
8分
16. 解不等式
．（8分）
解：因为对任意
，
，
所以原不等式等价于
． 3分
即
，
，
， 5分
故解为
．
所以原不等式的解集为
． 8分
17．已知a, b都是正数，并且a ¹ b，求证：a5 + b5 > a2b3 + a3b2 （9分）
证明：(a5 + b5 ) - (a2b3 + a3b2)
= ( a5 - a3b2) + (b5 - a2b3 )
= a3 (a2 - b2 ) - b3 (a2 - b2) 3分
= (a2 - b2 ) (a3 - b3) 4分
= (a + b)(a - b)2(a2 + ab + b2) 6分
∵a, b都是正数
∴a + b, a2 + ab + b2 > 0
又∵a ¹ b，
∴(a - b)2 > 0
∴(a + b)(a - b)2(a2 + ab + b2) > 0
即 a5 + b5 > a2b3 + a3b2 9分
18．已知圆E经过点A（2，－3）、B（－2，－5），且圆心在直线x－2y－3＝0上. （10分）
（1）求圆E的方程；
（2）若直线x＋y＋m＝0与圆E交于P、Q两点，且 EP⊥EQ，求m的值
解：（1）线段AB中垂线的方程为2x＋y＋4＝0
它与直线x－2y－3＝0的交点（－1，－2）为圆心 2分
由两点间距离公式得r2＝10 4分
所以，圆的方程为（x＋1）2＋（y＋2）2＝10 5分
（2）设圆心到直线的距离为d，由题意
即
8分
得
10分
19．已知圆的方程是：
,其中
,且
．（9分）
（1）求证：取不为1的实数时，上述圆恒过定点；
（2）求圆心的轨迹方程
（3）求恒与圆相切的直线的方程；
解：（1）将方程
整理得：
令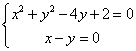
解之得
定点为
（2）圆心坐标为(，2-)，又设圆心坐标为(x，y)，
则有
消去参数得
即所求的圆心的轨迹方程为
（3）圆的圆心坐标为（，
），半径为
显然，满足题意切线一定存在斜率，
可设所求切线方程为，即
，
则圆心到直线的距离应等于圆的半径，即
恒成立，
即
恒成立比较系数得
解之得
，所以所求的直线方程为