高二数学（必修5） 不等式测试题
一、选择题：
1、若
，且
，则下列不等式一定成立的是 （ ）
A．
B．
C．
D．
2、函数
的定义域为 （ ）
A．
B．
C．
D．
3、已知
，则
（ ）
A．
B．
C．
D．
4、不等式
的解集为 （ ）
A．
B．
C．
D．
5、已知等比数列
的各项均为正数，公比
，设
，
，则P与Q的大小关系是
（ ）
A．P > Q B．P < Q C．P = Q D．无法确定
6、已知正数x、y满足
，则
的最小值是
（ ）
Ａ．18 Ｂ．16 C．8 D．10
7、下列命题中正确的是 ( )
A．当
B．当
，
C．当
，
的最小值为
D．当
无最大值
8、设直角三角形两直角边的长分别为a和b，斜边长为c，斜边上的高为h，则
和
的大小关系是
( )
Ａ．
Ｂ．
C．
D．不能确定
9、在约束条件
下，当
时，目标函数
的最大值的变化范围是
（ ）
A．
B．
C．
D．
10、若关于
的不等式
对任意
恒成立，则 实数
的取值范围是（ ）
A．
B．
C．
D．
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
二、填空题
11、设
满足
且
则
的最大值是
。
12、已知变量满足约束条件1≤
≤4,－2≤
≤2。若目标函数
仅在点(3,1)处取得最大值，则a的取值范围为___________.
13、设a＞0，且a
1，函数f(x)=alg（x2 －2a+1）有最小值,则不等式loga(x2－5x+7) ＞0的解集为___________.
14、某公司一年购买某种货物400吨，每次都购买吨，运费为4万元/次，一年的总存储费用为
万元，要使一年的总运费与总存储费用之和最小，则
_______
三、解答题
15、已知a, b都是正数，并且a ¹ b，求证：a5 + b5 > a2b3 + a3b2
16、关于x的不等式
的解集为空集，求实数k的取值范围.
17、已知正数
满足
,求
的最小值有如下解法：
解：∵
且
.∴ 
∴
. 判断以上解法是否正确？说明理由；若不正确，请给出正确解法．
19、制订投资计划时，不仅要考虑可能获得的盈利，而且要考虑可能出现的亏损，某投资人打算投资甲、乙两个项目，根据预测，甲、乙项目可能出的最大盈利率分别为100%和50%，可能的最大亏损率分别为30%和10%，投资人计划投资金额不超过10万元，要求确保可能的资金亏损不超过1.8万元，问投资人对甲、乙两个项目各投资多少万元？才能使可能的盈利最大？
18、已知函数
，当
时，
；当
时，
。①求a、b的值；②设
，
则当k 取何值时, 函数F(x)的值恒为负数?
20、某公司按现有能力，每月收入为70万元，公司分析部门测算，若不进行改革，入世后因竞争加剧收入将逐月减少．分析测算得入世第一个月收入将减少3万元，以后逐月多减少2万元，如果进行改革，即投入技术改造300万元，且入世后每月再投入1万元进行员工培训，则测算得自入世后第一个月起累计收入
与时间n（以月为单位）的关系为=
，且入世第一个月时收入将为90万元，第二个月时累计收入为170万元，问入世后经过几个月，该公司改革后的累计纯收入高于不改革时的累计纯收入．
高二数学（必修5）不等式参考答案
参考答案：1——10 DBAAA ABACA
11、 2 12、 (1，+∞) 13、 （2，3） 14、 20
3、若a<0，则
在
上为减函数，∵
，∴
6、解法一：（利用均值不等式）
,
当且仅当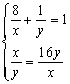
即
时“=”号成立，故此函数最小值是18。
解法二：（消元法）由
得
，由
则
当且仅当
即
时“=”号成立，故此函数最小值是18。
8、由面积公式可知
，则
＝
＝
＝
<0
9、分析：由
可得交点为：
①
当
时可行域是四边形OABC，
此时，
②当
时可行域是△OA
此时，
，故选D.
10、因函数
在上得最小值为－3，故
11、由
，即
。
故=
12、分析：由约束条件1≤≤4,－2≤≤2在坐标
系中画出可行域，如图为四边形ABCD，其中A(3，1)，
，目标函数
（其中
）
中的z表示斜率为－a的直线系中的截距的大小，若仅
在点
处取得最大值，则斜率应小于
，即
，
所以
的取值范围为(1，+∞)。
13、由函数f(x)=alg（x2 －
有最小值，
而
，故
，因此
。
所以求不等式loga(x2－5x+7) ＞0解可转化为求0<x2－5x+7<1的解。
14、该公司一年购买某种货物400吨，每次都购买吨，则需要购买
次，运费为4万元/次，一年的总存储费用为万元，一年的总运费与总存储费用之和为
万元，≥160，当
即20吨时，一年的总运费与总存储费用之和最小。
15、证明：(a5 + b5 ) - (a2b3 + a3b2) = ( a
= a3 (a2 - b2 ) - b3 (a2 - b2) = (a2 - b2 ) (a3 - b3)
= (a + b)(a - b)2(a2 + ab + b2)
∵a, b都是正数，∴a + b, a2 + ab + b2 > 0
又∵a ¹ b，∴(a - b)2 > 0 ∴(a + b)(a - b)2(a2 + ab + b2) > 0
即：a5 + b5 > a2b3 + a3b2
16、分析:本题考查含参数的“形式”二次不等式的解法.关键是对
前系数分类讨论.
解:(1)当
时，原不等式化为8<0，显然符合题意。
(2)当
时,要使二次不等式的解集为空集,则必须满足：
解得
综合(1)(2)得
的取值范围为
。
17、解：错误.
∵ 
① 等号当且仅当
时成立，又∵
②
等号当且仅当
时成立，而①②的等号同时成立是不可能的.
正确解法：∵且.
∴ 
，
当且仅当
，即
，又，∴这时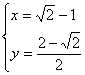
∴ 
．
18、解：设分别向甲、乙两项目投资万元，y万元，由题意知
 |
目标函数
作出可行域，作直线
，并作平行于直线
的一组直线
，
，与可行域相交，其中有一条直线经过可行域上的M点，且与直线
的距离最大，这里M点是直线
和0.3x+0.1y=1.8的交点，解方程组
解得x=4,y=6，此时z=1×4+0.5×6=7（万元） ∵7>0 ∴当x=4、y=6时z取得最大值。
答：投资人用4万元投资甲项目、6万元投资乙项目，才能在确保亏损不超过1.8万元的前提下，使可能的盈利最大。
19、解：（1）先作出符合条件下函数的大致图象，如图所示，
根据图象列出关于函数解析式的参数a，b的关系式。
∵
又∈（－2，6），
＞0；∈（－∞，－2）∪（6，+∞），＜0。
∴－2和6是方程
的两根。
故
解得
此时，
∴欲使＜0恒成立，只要使
恒成立，则须要满足：
①当时，原不等式化为
，显然不合题意，舍去。
②当时,要使二次不等式的解集为
，则必须满足：
解得
综合①②得的取值范围为
。
20、解：入世改革后经过n个月的纯收入为
万元
不改革时的纯收入为
又
由题意建立不等式
即
故取
答：经过13个月改革后的累计纯收入高于不改革时的累计纯收入．
＝