(数学选修1-1)第一章 常用逻辑用语 [提高训练C组]及答案
一、选择题
1.有下列命题:①![]() 年
年![]() 月
月![]() 日是国庆节,又是中秋节;②
日是国庆节,又是中秋节;②![]() 的倍数一定是
的倍数一定是![]() 的倍数;
的倍数;
③梯形不是矩形;④方程![]() 的解
的解![]() 。其中使用逻辑联结词的命题有( )
。其中使用逻辑联结词的命题有( )
A.![]() 个 B.
个 B.![]() 个 C.
个 C.![]() 个 D.
个 D.![]() 个
个
2.设原命题:若![]() ,则
,则![]() 中至少有一个不小于
中至少有一个不小于![]() ,则原命题与其逆命题
,则原命题与其逆命题
的真假情况是( )
A.原命题真,逆命题假 B.原命题假,逆命题真
C.原命题与逆命题均为真命题 D.原命题与逆命题均为假命题
3.在△![]() 中,“
中,“![]() ”是“
”是“![]() ”的( )
”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
4.一次函数![]() 的图象同时经过第一、三、四象限的必要但不充分条件是( )
的图象同时经过第一、三、四象限的必要但不充分条件是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.设集合![]() ,那么“
,那么“![]() ,或
,或![]() ”是“
”是“![]() ”的( )
”的( )
A.必要不充分条件 B.充分不必要条件
C.充要条件 D.既不充分也不必要条件
6.命题![]() 若
若![]() ,则
,则![]() 是
是![]() 的充分而不必要条件;
的充分而不必要条件;
命题![]() 函数
函数![]() 的定义域是
的定义域是![]() ,则( )
,则( )
A.“![]() 或
或![]() ”为假 B.“
”为假 B.“![]() 且
且![]() ”为真
”为真
C.![]() 真
真![]() 假 D.
假 D.![]() 假
假![]() 真
真
二、填空题
1.命题“若△![]() 不是等腰三角形,则它的任何两个内角不相等”的逆否命题
是
;
不是等腰三角形,则它的任何两个内角不相等”的逆否命题
是
;
2.用充分、必要条件填空:①![]() 是
是![]() 的
的
②![]() 是
是![]() 的
的
3.下列四个命题中
①“![]() ”是“函数
”是“函数![]() 的最小正周期为
的最小正周期为![]() ”的充要条件;
”的充要条件;
②“![]() ”是“直线
”是“直线![]() 与直线
与直线![]() 相互垂直”的充要条件;
相互垂直”的充要条件;
③ 函数![]() 的最小值为
的最小值为![]()
其中假命题的为 (将你认为是假命题的序号都填上)
4.已知![]() ,则
,则![]() 是
是![]() 的__________条件。
的__________条件。
5.若关于![]() 的方程
的方程![]() .有一正一负两实数根,
.有一正一负两实数根,
则实数![]() 的取值范围________________。
的取值范围________________。
三、解答题
1.写出下列命题的“![]() ”命题:
”命题:
(1)正方形的四边相等。
(2)平方和为![]() 的两个实数都为
的两个实数都为![]() 。
。
(3)若![]() 是锐角三角形, 则
是锐角三角形, 则![]() 的任何一个内角是锐角。
的任何一个内角是锐角。
(4)若![]() ,则
,则![]() 中至少有一个为
中至少有一个为![]() 。
。
(5)若![]() 。
。
2.已知![]() ;
;![]() 若
若![]() 是
是![]() 的必要非充分条件,求实数
的必要非充分条件,求实数![]() 的取值范围。
的取值范围。
3.设![]() ,
,
求证:![]() 不同时大于
不同时大于![]() .
.
4.命题![]() 方程
方程![]() 有两个不等的正实数根,
有两个不等的正实数根,
命题![]() 方程
方程![]() 无实数根。若“
无实数根。若“![]() 或
或![]() ”为真命题,求
”为真命题,求![]() 的取值范围。
的取值范围。
(数学选修1-1) 第一章 常用逻辑用语 [提高训练C组]
一、选择题
1.C ①中有“且”;②中没有;③中有“非”;④ 中有“或”
2.A 因为原命题若![]() ,则
,则![]() 中至少有一个不小于
中至少有一个不小于![]() 的逆否命题为,若
的逆否命题为,若![]() 都小于
都小于![]() ,则
,则![]() 显然为真,所以原命题为真;原命题若
显然为真,所以原命题为真;原命题若![]() ,则
,则![]() 中至少有一个不小于
中至少有一个不小于![]() 的逆命题为,若
的逆命题为,若![]() 中至少有一个不小于
中至少有一个不小于![]() ,则
,则![]() ,是假命题,反例为
,是假命题,反例为![]()
3.B 当![]() 时,
时,![]() ,所以“过不去”;但是在△
,所以“过不去”;但是在△![]() 中,
中,
![]() ,即“回得来”
,即“回得来”
4.B 一次函数![]() 的图象同时经过第一、三、四象限
的图象同时经过第一、三、四象限
![]() ,但是
,但是![]() 不能推导回来
不能推导回来
5.A “![]() ,或
,或![]() ”不能推出“
”不能推出“![]() ”,反之可以
”,反之可以
6.D 当![]() 时,从
时,从![]() 不能推出
不能推出![]() ,所以
,所以![]() 假,
假,![]() 显然为真
显然为真
二、填空题
1.若△![]() 的两个内角相等,则它是等腰三角形
的两个内角相等,则它是等腰三角形
2.既不充分也不必要,必要 ①若![]() ,
,![]()
②![]() 不能推出
不能推出![]() 的反例为若
的反例为若![]() ,
,
![]()
![]() 的证明可以通过证明其逆否命题
的证明可以通过证明其逆否命题![]()
3.①,②,③ ①“![]() ”可以推出“函数
”可以推出“函数![]() 的最小正周期为
的最小正周期为![]() ”
”
但是函数![]() 的最小正周期为
的最小正周期为![]() ,即
,即![]()
② “![]() ”不能推出“直线
”不能推出“直线![]() 与直线
与直线![]() 相互垂直”
相互垂直”
反之垂直推出![]() ;③ 函数
;③ 函数![]() 的最小值为
的最小值为![]()
令![]()
4.充要 ![]()
5.![]()
![]()
三、解答题
1.解(1)存在一个正方形的四边不相等;(2)平方和为![]() 的两个实数不都为
的两个实数不都为![]() ;
;
(3)若![]() 是锐角三角形, 则
是锐角三角形, 则![]() 的某个内角不是锐角。
的某个内角不是锐角。
(4)若![]() ,则
,则![]() 中都不为
中都不为![]() ;
;
(5)若![]() 。
。
2.解:![]()
![]()
![]() 是
是![]() 的必要非充分条件,
的必要非充分条件,![]()
![]()
![]() ,即
,即![]() 。
。
3.证明:假设![]() 都大于
都大于![]() ,即
,即![]()
![]() ,而
,而![]()
![]() 得
得![]()
即![]() ,属于自相矛盾,所以假设不成立,原命题成立。
,属于自相矛盾,所以假设不成立,原命题成立。
4.解:“![]() 或
或![]() ”为真命题,则
”为真命题,则![]() 为真命题,或
为真命题,或![]() 为真命题,或
为真命题,或![]() 和
和![]() 都是真命题
都是真命题
当![]() 为真命题时,则
为真命题时,则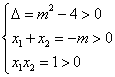 ,得
,得![]() ;
;
当![]() 为真命题时,则
为真命题时,则![]()
当![]() 和
和![]() 都是真命题时,得
都是真命题时,得![]()
![]()