平面与平面平行垂直和二面角单元测试卷

《平面与平面平行﹑垂直和二面角》单元测试卷

一、　　　　　　 选择题

1.下列命题中正确的是(　　　 ).

A.夹在两个平行平面间的相等线段必平行

B.夹在两个平行平面间的平行线段相等

C.两个平面分别和第三个平面相交,若两条交线平行,则这两个平面平行

D.平行于同一条直线的两个平面互相平行

2.设直线a平面,则平面平行于平面是直线a平行于平面的(　　　 )

A.充分不必要条件　　　　B.必要不充分条件

C.充要条件　　　　　　  D.既不充分也不必要条件

3.过空间一点的三条直线两两垂直，则它们确定的平面互相垂直的对数有（　　　）。

A．0　　　B.1　　　 C.2　　　　D.3

4.下列命题中错误的是(　　　　).

A.如果平面⊥平面，那么内所有直线都垂直于平面

B.如果平面⊥平面，那么内一定存在直线平行于平面

C.如果平面不垂直于平面，那么内一定不存在直线垂直于平面

D.如果平面⊥平面，平面⊥平面，，那么平面

5.已知二面角A-BC-D，A-CD-B，A-BD-C的平面角都相等，则点A在平面BCD上的射影是

 △BCD的（　　　 ）。

A.内心　　 B.外心　　 C.垂心　　  D.重心

6.自二面角内一点分别向两个半平面引垂线，它们所成的角与二面角的平面角的大小关系是（　　　 ）。

A.相等　　 B.互补　　 C.无关　　  D.相等或互补

7.设m,n是两条不同的直线,是三个不同的平面,给出下列四个命题:①若m,n∥,则m⊥n;②若∥,∥,m⊥,则m;③若m∥,n∥,则m∥n;④若则∥.其中正确命题的序号是（　　　 ）

A.②③　　　　　 B. ①②　　　　　 C.③④　　　　　 D. ①④

8.正方体EFGH-E₁F₁G₁H₁中，下列各对截面，彼此平行的一对是（　　　　）

A.面E₁FG₁与面EGH₁　　　　　　　  B. 面FHG₁与面F₁H₁G

C. 面F₁H₁H与面FHE₁　　　　　　　 D. 面E₁HG₁与面EGH₁

9.下列条件中，能判定平面∥平面的是(　　　　).

A.存在两条相交直线分别与，成等角

B.内有不在同一条直线上的三个点到的距离相等

C.内有△ABC与内△A₁B₁C₁全等，且有AA₁∥BB₁∥CC₁

D.，都与异面直线a,b平行

10.将锐角A为60°，边长为的菱形ABCD沿对角线BD折成60°的二面角，则AC与BD的中点O的距离为（　　　）。

A.　　　　  B.　　　　　 C.　　　　　　  D.

11.二面角-MN-的平面角为,AB,B∈MN,∠ABM=(为锐角),AB与平面所成角为，则下列关系式成立的是（　　　）。

A.　　　　　　  B.　　　　　　　　

C.　　　　　 　　D.

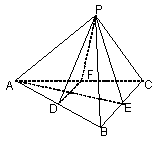
12.在正四面体P-ABC中，D，E，F分别是AB，BC，CA的中点，下列四个结论中不成立的是（　　　 ）。

A.BC∥平面PDF　　　　　　　　 B. DF⊥平面PAE

C.平面PDF∥平面ABC　　　　　  D. 平面PAE⊥平面ABC

二、　　　　　　 填空题

13.设∥，A，C∈，B，D∈，直线AB与CD交于点S，且AS=8，BS=9，CD=34，当S在，之间时，CS=______________

14. 一条直线与直二面角的两个面所成的角分别为和，则+的取值范围为______________

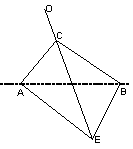
15.如图，有一个三角形的遮阳棚△ABC，AC=3m，BC=4m，AB=5m，

A，B是安置在地面上南北方向的两个定点，由正西方向的太

阳（用点O表示）射出的光线OCE与地面成30°的角，△ABE

为遮阳棚产生的阴影，当遮阳棚与地面构成60°的二面角时，

该遮阳棚所遮阴影△ABE的面积是______________

16.已知直线⊥平面，直线平面，则下列命题：

①若∥，则；②若，则⊥；③若∥，则⊥；④若，则∥。其中正确的命题为______________（写出序号即可）。

三、　　　　　　 解答题

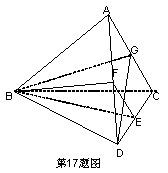
17.如图，在空间四边形ABCD中，AB=BC，CD=DA，E，F，G分别为CD，DA和对角线AC的中点，求证：平面BEF⊥平面BGD。

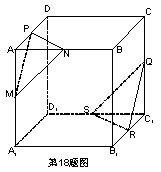
18.如图，ABCD-A₁B₁C₁D₁是棱长为的正方体，M，N，P，Q，R，S分别是AA₁，AB，AD，CC₁，B₁C₁，C₁D₁的中点，求证：平面PMN∥平面QRS。

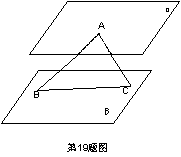
19.如图，平面∥，AB和AC是夹在平面与之间的两条线段，AB⊥AC，且AB=2，直线AB与平面所成角为30°，求线段AC长的取值范围。

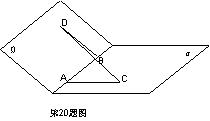
20.如图,已知二面角为120°, ,且AC⊥AB,BD⊥AB,AB=AC=BD=a,求:(1)CD的长;(2)CD与AB所成的角.

21.在四面体ABCD中,AB=AD=,BC=CD=3,AC=,BD=2.

(1)平面ABD与平面BCD是否垂直？证明你的结论；

（2）求二面角A-CD-B的正切值。

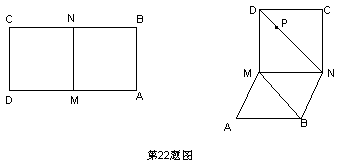
22.如图，已知矩形ABCD，M，N分别是AD，BC的中点，且AM=AB，将矩形沿MN折成直二面角，若P点是线段DN上一动点，求P到BM距离的最小值。

参考答案:

1.　　　 通过构造反例知选B.

2.　　　 当直线a平行于平面时，平面与平面可能相交，故选A。

3.　　　 三条直线确定的三个平面中，任意两个都互相垂直，故选D。

4.　　　 当平面⊥平面时，平面内垂直于与的交线的直线垂直于，不是内所有直线都垂直于，故选A。

5.　　　 由题意知点A在平面BCD上的射影到△BCD的三边距离相等∴A在平面BCD上的射影为△BCD的内心，故选A。

6.　　　 由条件知两垂线可确定一个平面，此平面和二面角的交线所成的角是二面角的平面角，此二面角的交线分别与垂线垂直，故选B。

7.　　　 对于①，由n∥可知，存在直线，使∥n，由m可知m,∴m⊥n∴①正确；对于②，由∥,∥得∥∵m⊥∴m∴②正确；对于③④可举出反例排除，故选B。

8.　　　 利用面面平行的判定定理知选A。

9.　　　 A中，可能相交；B中若内三点在两侧，则与相交；C中只有AA₁∥BB₁∥CC₁且AA₁=BB₁=CC₁时有∥，故选D。

10.　 在二面角内BD⊥OA,BD⊥OC,∴∠AOC为二面角的平面角, ∠AOC=60°.作OE⊥AC于E点,AO=CO=,故选A.

11.　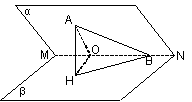 如图，过A作AH于H，作HO于O，连结AO，

则AO，∠AOH为-MN-的平面角，∠ABH为

AB与所成的角∵

,故选C。

12.　 如图，∵BC∥DF∴BC∥平面PDF,故A正确；

∵BC⊥PE，BC⊥AE∴BC⊥平面PAE

∴DF⊥平面PAE，故B正确；

∴平面PAE⊥平面ABC，故D正确。故选C。

13.　 ∵∥且AB∩CD=S，∴AC∥BD

∴AS：SB=CS：SD∵AS=8，BS=9，CD=CS+SD=34∴CS=16。

14.　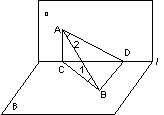 如图，∠1，∠2分别表示直线AB与直二面角的两

 个面所成的角，由最小角定理知∠1小于∠ABD

∵∠ABD+∠2=90°∴一般地，∠1+∠2＜90°。

特别地，当时，∠1+∠2=90°；

当AB∥时，∠1+∠2=0°。故填

15.　 由题知CE⊥AB，则作CD⊥AB于D点，则有DE⊥AB，即∠CDE就是二面角C-AB-E的平面角，∴∠CDE=60°，又CE与地面成30°角即∠CED=30°∴∠ECD=90°由CD=2.4m,则DE=4.8m,∴△ABE的面积是12m².

16.　利用面面垂直的判定定理与线面垂直的性质定理易知填①③。

17.　 ∵AB=BC，CD=DA， G为AC的中点∴BG⊥AC，DG⊥AC∴AC⊥平面BGD∵EF∥AC∴EF⊥平面BGD∵EF平面BEF∴平面BEF⊥平面BGD

18.　 连结BD，B₁D₁，则BD∥B₁D₁∵P，N分别为AD，AB的中点∴PN∥BD同理RS∥B₁D₁∴PN∥RS同理可证PM∥RQ∵PN∩PM=P，RS∩RQ=R∴平面PMN∥平面QRS。

19.　 作AD于D，连结BD，CD，BC。

∵AB＞BD，AC＞CD，AB²+AC²=BC²

∴在△BDC中，（*）

∵AD∴∠ABD是AB与所成的角∵∥∴∠ABD也是AB与所成的角

∴∠ABD=30°∵AB=2，∴AD=1，BD=，DC²=AC²-1，BC²=4+AC²代入（*）式得

∴

20.　 (1)过点B在内作BE∥AC且BE=AC，连结DE。∵AC⊥AB，AB=AC∴四边形ABEC为正方形∴EC∥AB且EC=AB=a,AB⊥BE∵BD⊥AB∴∠DBE为二面角的平面角

∴∠DBE=120°根据余弦定理得∵BD⊥AB，AB⊥BE∴AB⊥平面DBE∵CE∥AB∴CE⊥平面DBE∴CE⊥DE在Rt△DCE中，

（2）由（1）知CE∥AB，∴∠DCE为CD与AB所成的角，且CE⊥DE，，CE=a,∴tan∠DCE=DE:CE=又∵∠DCE为锐角∴∠DCE=60°即CD与AB所成的角为60°。

21.　 如图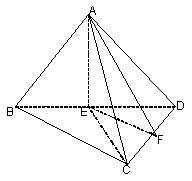，（1）垂直。证明如下:设BD的中点为E，连AE，CE。

∵AB=AD∴AE⊥BD。同理CE⊥BD。

∴AE=，

∵AC=,∴AC²=AE²+CE²∴∠AEC=90°即AE⊥EC

∴AE⊥平面BCD∵AE平面ABD∴平面ABD⊥平面BCD

(2)作EF⊥CD于F，连结AF。∵AE⊥平面BCD∴AF⊥CD

∴∠AFE就是二面角A-CD-B的平面角，

∴即二面角A-CD-B的正切值为。

22.　 如图,过P点作PE⊥MN，垂足为E，过E点作EF⊥BM于F点，连结PF。

由题意可知平面CDMN⊥平面ABMN，∴PE⊥平面ABMN∴PF在平面ABMN中的射影为EF，由三垂线定理知PF⊥BM，即PF的长为P到BM的距离。

设AM=AB=，PN=，则∵四边形ABNM是正方形∴,

在Rt△EFM中

在Rt△EFP中，

∴当时，有最小值为，即当点P位于距N点处时，P点到BM的距离取得最小值，这个最小值为.