高二文科数学下学期考试卷

高二文科数学下学期考试卷

时量：120分钟　 满分：150分

命题人：胡雪文　 　校审人：江楚珉

一、选择题（本大题共10小题，每小题5分，共50分.选对的得5分，错选或不答得0分.）

1．若直线a，b，c满足a∥b，b与c不平行，则（　　）

A．a与c平行　　　　　　　　　　　　　　　　　　　　　　　　　　　　B．a与c不平行

C．a与c是否平行不能确定　　　　　　　　　　　　　　　　 D．a与c是异面直线

2．随机事件A的概率P(A)满足　　　　　　　　　 (　　 )

A.P(A)=0　 　 　B.P(A)=1　　　　　 C.P(A)>1　　　　 D.

3．下列命题正确的是（　　）

A．一条直线与一个平面平行，它就和这个平面内的任意一条直线平行

B．平行于同一个平面的两条直线平行

C．与两个相交平面的交线平行的直线，必平行于这两个平面

D．平面外的两条平行直线中的一条与一个平面平行，则另一条直线也与此平面平行

4．空间四边形ABCD的四边相等，则它的两对角线AC、BD的关系是（　　）

A．垂直且相交　　 　　　　　　　　　　　　　　　　　　　　　B．相交但不一定垂直

C．垂直但不相交　 　　　　　　　　　　　　　　　　　　　D．不垂直也不相交

5．空间四边形OABC中，= a，= b，= c，点M是在OA上且OM = 2MA，N为BC的中点，则等于（　　）

A．ab +c　　　　　B．a +b +c　　　C．a +bc　　　　 D．a +bc

6．若直线l与平面所成角为，直线a在平面内，且与直线l异面，则直线l与直线a所成的角的取值范围是（　　）

A．　　　　　　　　　　B．　　　　　　　　 C．　 　　　　　　　D．

7．长方体的一个顶点处的三条棱长之比为1:2:3，它的表面积为88，则它的对角线长为（　　）

A．12　　　　　　　　　　　　　 B．24　　　　　　　　　　　　　C．　　　　　　　　　　 D．

8．二项式的展开式中的系数是 （  ）

A、6　　　 B、12　　　 C、24　　　　 D、48

9. 抛物线x²=y的准线方程为　　（　　）

A.x=－1　　　　 B.y=－1　　　　 C.x=　　　　  D.y=

10．设双曲线的焦点在x轴上，两条渐近线为y =±，则该双曲线的离心率e等于（　　）

A．5　　　　　　　　　　　　　 B．　　　　　　　　　　　　C．　　　　　　　　　　　 D．

二、填空题（每小题5分，共25分）

11．若A (1, –1, 1)，B (–2, 0, 3)，则= 　　　　　　　　　　　 .

12．过抛物线y² = 8x的焦点，倾斜角为45°的直线的方程是　　　　　　　　　　　　　　.

13．方程表示焦点在y轴上的椭圆，则m的取值范围是　　　　　　　　　　　　 .

14．正四面体A—BCD的棱长为1，则A到底面BCD的距离为　　　　　　 .

15．从分别写有A,B,C,D,E的5张卡片中,任取2张,这2张上的字母恰好按字母顺序相邻的概率为________________.

座位号

高二文科数学考试答卷

08年元月26日

年级

高二

科目

文科数学

时 量

120分钟

一、选择题（每小题5分，共50分） 题号 1 2 3 4 5 6 7 8 9 10 答案 二、填空题（每小题5分，共25分） 11．　　　 　 　　 　　　　12．　　　　　　　  　　　 13．　　　　　　 14．　　　　　　　 　　　15．　　　　　　　  三、解答题（75分） 16．（12分）如图，在正方体ABCD—A1B1C1D1中，点E是DD1的中点. （1）求证：AC⊥BD­1； （2）求证：BD1∥平面CEA. 17．（12分）△ABC的两个顶点A、B的坐标分别是(–6, 0)，(6, 0)，边AC、BC所在直线的斜率之积等于，求顶点C的轨迹.

年　 级

班　 次

姓　 名

考　 号

考室号

 

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

考　室 座位号 成　绩

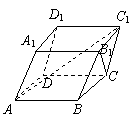18．（12分）在平行六面体ABCD—A₁B₁C₁D₁中，AB = AD = AA₁= 1，∠A₁AB =∠A₁AD =∠DAB = 60°.（1）求对角线AC_­1的长；

（2）求异面直线AC₁与B₁C的夹角.

19. (12分) 掷两枚骰子.(1)求出现的点数之和等于3的概率;(2)求出现的点数都为偶数的概率;(3)求出现的点数之和不超过4的概率。

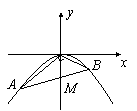20．（13分）抛物线上有两点A (x₁, y₁)，B (x₂, y₂)，且= 0，又知点M (0, –2). （1）求证：A、M、B三点共线； （2）若，求AB所在的直线方程.

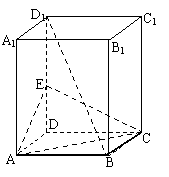
21．(14分)如图，在直三棱柱ABC—A₁B₁C₁中，∠ACB = 90°. AC = BC = a，D、E分别为棱AB、BC的中点，M为棱AA₁­上的点，二面角M—DE—A为30°.

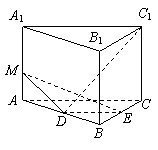（1）证明：A₁B₁⊥C₁D；

（2）求MA的长；

（3）求点C到平面MDE的距离.

湖南省邵东一中高二数学期末考试参考答案（文）

一、选择题（每小题5分，共50分）

1．B　　　2．D　　　3．D　　　4．C　　　5．B　　　6．D　　　7．C　　　8．C　　　9．D　　　

10．C　　　　　

二、填空题（每小题5分，共25分）

11．　　　　　　　12．x – y – 2 = 0　　　　　13．8＜m＜25　　 14．　　 15．

三、解答题

16．（12分）（1）证：∵棱柱ABCD—A₁B₁C₁D₁为正方体，∴D₁D⊥面ABCD，∴BD是BD₁在底面ABCD内的射影。又∵BD⊥AC，∴BD₁⊥AC。

（2）设AC∩BD = O，连结OE，∵O、E分别为BD、DD₁的中点，∴OE∥BD₁.

又∵BD₁平面CEA，OE平面CEA，∴BD₁∥平面CEA。

17．（12分）解：设顶点C的坐标为C(x, y)，则(x≠±6)

而k_AC·k_BC =，即，化简得=1 (x≠±6).

顶点C的轨迹是焦点在x轴长，长轴长为12，短轴长为8的椭圆，并去掉A、B两点.

18．（12分）解：（1）设= a，= b，= c，则a = b = c = 1，a，b=b，c=a，c= 60°，(a + b + c)² = a² + b² + c² + 2a·b + 2b·c + 2a·c = 6，∴.

（2）∵b – c，∴= (a + b + c)·(b – c) = a·b + b² + b·c–a·c–b·c–c² = 0.

∴，∴异面直线AC₁与B₁C的夹角为90°.

19．（12分）解：

(1).令点数和为3的事件为A,掷两枚骰子可能出现的情况：（1，1），（1，2），…，（1，6），（2，1），（2，2），…，（2，6），…，（6，1），（6，2），…，（6，6），基本事件总数为6×6=36。

在这些结果中，有利于事件A的只有两种结果（1，2），（2，1）。

.

　(2);　 (3) (过程略)

20．（13分）解：设，∵，∴= 0 (x₁x₂≠0).

∴x₁x₂ = – 4.

又∵，.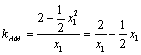

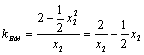代代入k_AM得，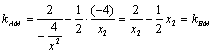

∴A、M、B三点共线.

（2）∵，∴

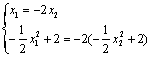
∴，∴. 即或.

∴或，AB的方程为.

21．(14分)解：（1）连结CD.

∵三棱柱ABC—A₁B₁C₁是直三棱柱，

∴CC₁⊥平面ABC，

∴CD为C₁D在平面ABC内的射影.

∵△ABC中，AC = BC，D为AB中点.

∴AB⊥CD，∴AB⊥C₁D，∵A₁B₁∥AB. ∴A₁B₁⊥C₁D.

（2）解：过点A作CE的平行线，交ED的延长线于F，连结MF.

∵D、E分别为AB、BC的中点， ∴DE∥AC.　 又∵AF∥CE，CE⊥AC，

∴AF⊥DE.　　∵MA⊥平面ABC.　　∴AF为MF在平面ABC内的射影，

∴MF⊥DE，　 ∴∠MFA为二面角M—DE—A的平面角，∠MFA = 30°.

在Rt△MAF中，，∠MFA = 30°，　∴.

（3）设C到平面MDE的距离为h.

∵，　　 ∴，

，　，

∴，　∴，即C到平面MDE的距离为.