高二文科数学第一学期教学质量检测
高二数学试题(文科)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共 150分.考试时间120分钟.
第Ⅰ卷(选择题 共60分)
注意事项:
1.答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上.
2.每小题选出答案后,用铅笔把答题卡对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,不能答在试卷上.
3.考试结束,监考人将本试卷和答题卡一并收回.
参考公式:
![]() (其中R为外接圆半径)
(其中R为外接圆半径)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知等差数列10,7,4……,则该数列的第10项为 ( )
A.17 B.
2.![]() 的值为 ( )
的值为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.已知A为三角形的一个内角,且![]() 的值为 ( )
的值为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.数列![]() ,则a25等于 ( )
,则a25等于 ( )
A.570 B.
5.在△ABC中,若∠A=45°.![]() ,则满足条件△ABC ( )
,则满足条件△ABC ( )
A.不存在 B.有一个 C.有两个 D.个数不确定
6.已知△ABC的三内角A、B、C满足条件![]() ,则角A等于( )
,则角A等于( )
A.30° B.60° C.70° D.120°
7.已知三角形的两边之和为4,其夹角60°,则此三角形的周长最小时,这两边长分别为
( )
A.2,2 B.1,![]() D.
D.![]()
8.若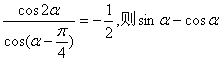 等于 ( )
等于 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.在等差数列![]() 则此数列前13项的和为( )
则此数列前13项的和为( )
A.13 B.
10.已知数列![]() ,则数列
,则数列![]() 的通项为
的通项为
|
A.![]() B.
B.![]()
C.![]() D.
D.![]()
11.在等比数列![]() ( )
( )
A.-2 B.-2或![]() D.
D.![]()
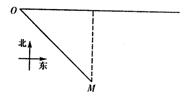
12.一船向正北航行,看见正西方有两个灯塔恰好与它在一条直线上,两塔相距10海里,继续航行半小时后,看见一塔在船的南60°西,另一塔在船的南45°西,则船速(海里/小时)是 ( )
A.5 B.![]() C.10 D.10
C.10 D.10![]() +10
+10
|
注意事项:
1.用钢笔圆珠笔直接答在试题卷中.
2.答卷前将密封线内的项目填写清楚.
二、填空题:本大题共4小题,每小题4分,共16分.把答案填在题中横线上.
13.△ABC的三个内角A,B,C所对的边分别是a,b,c,设向量![]() ,
,![]() ,若p//q,则角C等于
.
,若p//q,则角C等于
.
14.已知数列![]() ,则该数列的通项公式为
.
,则该数列的通项公式为
.
15.某地有适宜造林的荒地2640万亩,从2007年开始绿化造林,第一年绿化120万亩,以后每年比前一年多绿化60万亩,则到 年底可绿化全部荒地.
|
.
三、解答题:本大题共6小题,共74分.解答应写出相应的文字说明,证明过程或演算步骤.
17.(本小题满分12分)已知等差数列![]()
(1)求数列![]() 的通项公式;
的通项公式;
(2)记数列![]() 的前n项和记为Sn,求Sn.
的前n项和记为Sn,求Sn.
18.(本题满分12分)已知![]() .
.
(1)求![]() 的值;
的值;
(2)求![]() 的值.
的值.
19.(本小题满分12分)已知![]() 的图象上,数列
的图象上,数列![]() 满足
满足![]() .
.
(1)求数列![]() 的通项
的通项![]() ;
;
(2)当数列![]() 的前n项和最小时,求n的值.
的前n项和最小时,求n的值.
20.(本小题满分12分)在△ABC中,角A、B、C的对边分别为a,b,c,且满足![]() 的面积S=10
的面积S=10![]()
(1)求角C;
(2)求a、b的值.
|
米,且与海岸线距离400千米的海面上M点处有一艘
快艇与汽车同时出发,要把一件重要物品送给这辆汽车
司机.该快艇至少以多大的速度行驶,才能将物品送到司
机手中?并求出此时快艇行驶的方向.
(参考数据:![]() )
)
22.(本小题满分14分)已知正数列![]() 的前n项和为
的前n项和为![]() ,数列
,数列![]() 是首项为1,公比为
是首项为1,公比为![]() 的等比数列.
的等比数列.
(1)求证数列![]() 是等差数列;
是等差数列;
(2)若![]() 的前n项和Tn;
的前n项和Tn;
(3)在(2)条件下,是否存在常数![]() ,使得数列
,使得数列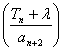 为等比数列?若存在,试求出
为等比数列?若存在,试求出![]() ;若不存在,说明理由.
;若不存在,说明理由.
山东省潍坊市2007-2008学年第一学期教学质量检测
高二数学试题(文科)参考答案
一、选择题:本大题共12小题,每小题5分,共60分.
|
二、填空题:本大题共4小题,每小题4分,共16分.把答案填在题中横线上.
13.60° 14.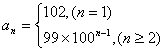 15.2014
15.2014
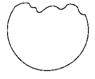
16.方案一:①作圆块内接△ABC;
②用直尺量出边长a,用量角器量出对角A.
③用正弦定理求出直径:2R=![]()
方案二:①作圆块内接△ABC;
②用直尺量出三边的长a,b,c,用余弦定理求出角A;
③由正弦不定理可求出直径:![]()
三、解答题:本大题共6小题,共74分.
17.(本小题满分12分)
解:(1)由题意得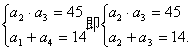 ……………………2分
……………………2分
解得 ……………………4分
……………………4分
![]()
![]() ……………………6分
……………………6分
(2)由(1)得![]()
![]() ……………………8分
……………………8分
![]()
![]() ……………………10分
……………………10分
![]()
![]() ……………………12分
……………………12分
18.(本小题满分12分)
解(1)![]()
![]()
![]() ……………………2分
……………………2分
![]()
![]()
![]()
![]() …………………………5分
…………………………5分
(2)![]()
=![]()
![]() …………………………7分
…………………………7分
![]()
![]() …………………………10分
…………………………10分
![]()
![]()
=-1……………………12分
19.(本小题满分12分)
解:(1)依题意:![]() ……………………2分
……………………2分
![]() ……………………4分
……………………4分
当n=1时,S1=a1=1,……………………4分
![]() ……………………6分
……………………6分
(2)![]()
![]() 为等差数列.……………………8分
为等差数列.……………………8分
![]() ……………………10分
……………………10分
故当n=12或13时,数列![]() 的前n项和最小.……………………12分
的前n项和最小.……………………12分
20.(本小题满分12分)
解:(1)![]()
![]() ……………………2分
……………………2分
![]()
![]()
![]()
![]() ……………………4分
……………………4分
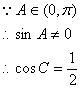
![]() .……………………6分
.……………………6分
(2)由![]()
得ab=40.①……………………8分
由余弦定理,得:
![]()
即![]()
![]()
![]() ②……………………10分
②……………………10分
由①②得a=8,b=5或a=5,b=8.…………………………12分
21.(本小题满分12分)
|
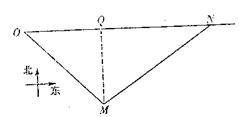
度出发,沿MN方向航行,t小时后在N点与汽
车相遇,MQ为M点到ON的距离,则MQ=400,
在△MON中,MO=500,ON=100t,MN=vt
设∠MON=![]() ,由题意知
,由题意知![]()
……………………2分
由余弦定理,得MN2=OM2+ON2-2OM·ON·cos![]()
即![]() ……………………2分
……………………2分
![]() ………………6分
………………6分
当![]() 即快艇必须至少以80千米/小时速度行驶,
即快艇必须至少以80千米/小时速度行驶,
此时MN=![]() ……………………9分
……………………9分
设∠NMQ=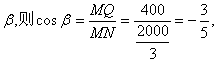 ……………………11分
……………………11分
故快艇的行驶方向为北偏东53°08′.……………………12分
另解提示:在△OMN中,
![]()
∴当![]()
22.(本小题满分14分)
解:(1)由![]() ,
,
当n=1时,![]()
![]() ……………………1分
……………………1分
当![]() ,
,
![]() ,
,
即![]() ………………3分
………………3分
![]()
即![]()
![]() 的等差数列……………………4分
的等差数列……………………4分
(2)依题意![]()
![]()
![]()
![]()
![]()
![]()
![]() ①
①
![]() ,②……………………8分
,②……………………8分
①—②得![]()
![]()
![]() …………………………10分
…………………………10分
(3)![]()
=![]() ……………………12分
……………………12分
要使数列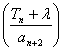 为等比数列,当且仅当
为等比数列,当且仅当![]() 时
时
故存在![]() ,使
,使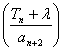 为等比数列……………………14分
为等比数列……………………14分