高二（文科）数学第一学期期中试卷
（试卷I） 命题 邱形贵 审核 刘水明
一、选择题（每题只有一个正确答案，把选项代号填入答卷中每题5分。满分60分）
1．不等式“
”成立的一个充分条件是（
）
A．
B．
C．
D．
2．设定点
（－3，0）、
（3，0），动点
满足条件
，则点的轨迹是（ ）
A．椭圆 B．不存在 C．椭圆或线段 D．线段
3．
在
中,若
则的形状一定是（ ）
A. 等腰直角三角形 B.等腰三角形 C. 直角三角形 D. 等边三角形
4．在等差数列
中，
为前n项和，且
，则n为（ ）
A．2 B．
5．设集合
是三角形的三边长}，则
所表示的平面区域（不含边界的阴影部分）是（ ）
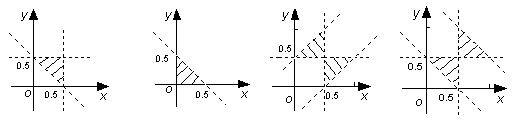
A． B． C． D．
6．若
，
，则
，2
，
，
中最大一个是 （ ）
A． B． C． D．
7．“
”的含义为（ ）
A．
、
都不为
B．、至少有一个为
C．、至少有一个不为 D．不为且为，或不为且为
8．满足条件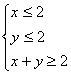
的
的取值范围是（ ）
A．[2,6] B．[2,5] C．[3,6] D．[3,5]
9．到两坐标轴的距离相等的动点的轨迹方程是（ ）
A．
B．
C．
D．
10．一个圆的圆心为椭圆的右焦点，且该圆过椭圆的中心交椭圆于P,直线PF
（F为椭圆的左焦点）是该圆的切线，则椭圆的离心率为（ ）
A．
B．
C．
D．
11．甲、乙两工厂2007年一月份产值相同，甲厂的产值逐月增加，且每月增加的产值相等，乙厂的产值也逐月增加，且每月增长的百分率相等，已知2007年三月份两厂的产值又相等，则2007年二月份产值高的工厂是（ ）
A．产值一样 B．乙厂 C．甲厂 D．无法确定
12．在R上定义运算
，若不等式
对任意
成立，则实数的取值范围是（ ）
A．
B．
C．
D．
二、填空题(4小题，共16分。只要求在答卷中直接填写结果，每题填对得4分．)
13．已知命题
：
，命题
：
，又
为真，则范围为
14．命题P：
。则
为
15．椭圆一焦点为（0，
），且短轴长为4的椭圆标准方程是
16．
|
表（每行比上一行多一个数）：设
（i、j∈N*）是位于
这个三角形数表中从上往下数第i行、从左往右数第j个数，
如
＝8．则
为
泉州一中07—08学年度第一学期期中试卷
高 二（文科）数学（试卷II） 命题 邱形贵 审核 刘水明 
| 题号 | 一 | 二 | 三 | 总分 | |||||
| 17 | 18 | 19 | 20 | 21 | 22 | ||||
| 得分 | |||||||||
一、 选择题(60分，每题5分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 选项 |
二、填空题（20分，每题4分）
13． ；14． ；
15． ；16．
三、解答题（6小题，共74分。在答卷中应写出文字说明，证明过程或演算步骤）
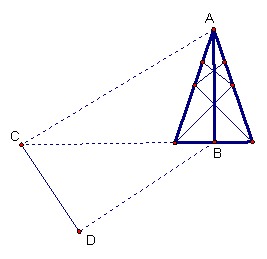17．如图，测量河对岸的塔高
时，可以选与塔底
在同一水平面内的两个测点
与
．现测得
，并在点测得塔顶的仰角为
，求塔高。(12分)
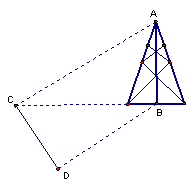
18．△ABC中，AB＝5，AC＝3，∠A＝120o，求以点B、C为焦点且过点A的椭圆方程。(12分)
19．现有一批货物用轮船甲地运往乙地距离为500海里，已知该船最大速度为45海里/小时，每小时运输成本由燃料费用和其他费用组成。轮船速度x(海里/小时)时，则每小时燃料费用为
（
），其余费用为每小时960元。已知轮船速度为20海里/小时的全程运输成本为30000元。(12分)
（1）把全程运输成本y（元）表示为速度x(海里/小时)的函数；
（2）为了使全程运输成本最小，轮船应为多大速度行驶？
20．数列中
，且由下列条件确定：
．(12分)
（1）证明：对n≥2，总有
；
（2）证明：对n≥2，总有
．
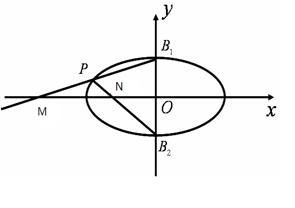
21．为椭圆
上的任意一点（异于顶点），椭圆短轴上两个端点分别是
若直线
分别与轴交于点
，求证：
成等比。(12分)
22．已知正项数列满足
=P(0<P<1)，且
(14分)
(1)若
，求证：数列
为等差数列；
(2)求证：
.
泉州一中07—08学年度第一学期期中试卷
高 二（文科） 数 学 参考答案
二、 选择题(60分，每题5分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 选项 | C | D | B | B | A | A | C | A | C | D | C | B |
二、填空题（20分，每题4分）
13． 
14．
15． 
16．
2007
三、解答题（本题共6小题，共74分.在答卷中应写出文字说明，证明过程或演算步骤）
17．如图，测量河对岸的塔高时，可以选与塔底在同一水平面内的两个测点与．现测得，并在点测得塔顶的仰角为，求塔高。(12分)
解：在
中，
2分
由正弦定理得
5分
所以
．
8分
在
中，
． 12分
18．△ABC中，AB＝5，AC＝3，∠A＝120o，求以点B、C为焦点且过点A的椭圆方程。(12分)
解：由余弦定理得：
2分
即
得
4分
以BC为x轴，BC垂直平分线为y轴建立直角坐标系 6分
由椭圆定义知
，
8分
知
10分
故椭圆方程为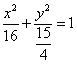
12分
19．现有一批货物用轮船甲地运往乙地距离为500海里，已知该船最大速度为45海里/小时，每小时运输成本由燃料费用和其他费用组成。轮船速度x(海里/小时)时，则每小时燃料费用为（），其余费用为每小时960元。已知轮船速度为20海里/小时的全程运输成本为30000元。(12分)
（1）把全程运输成本y（元）表示为速度x(海里/小时)的函数；
（2）为了使全程运输成本最小，轮船应为多大速度行驶？
解：（1）由题意得,全程所用时间为
小时。 1分
则全程运输成本y=
，
.
4分
当x=20时,y=30000得：k=0.6 5分
故所求的函数为y=
, 7分
(2)y=
, 10分
当且仅当
，即x=40时取等号。 11分
故当轮船速度为40海里/小时时，所需成本最小。 12分
20．数列中，且由下列条件确定：．(12分)
（1）证明：对n≥2，总有；
（2）证明：对n≥2，总有．
解：（1）证明：由
及
从而有
4分
所以，当n≥2，总有
≥
成立.
6分
（2）证法一：当
所以
10分
故当
12分
证法二：当
所以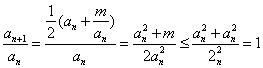
10分
故当.
12分
21．21．为椭圆上的任意一点（异于顶点），椭圆短轴上两个端点分别是若直线分别与轴交于点，求证：成等比。(12分)
解：由椭圆方程知
另设
2分
由M，P，B1三点共线，知
4分
所以
6分
同理得
9分
又在椭圆上所以
即
代入*，得
10分
=
＝
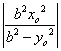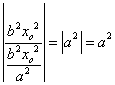12分
（或由向量共线，或由直线方程截距式等求得点M坐标可相应给分）
22．已知正项数列满足=P(0<P<1)，且
(14分)
(1)若，求证：数列为等差数列；
(2)求证：.
22．解：
(1)
1分
4分
故数列是以
为首项，以1为等差的等差数列
6分
（或由直接推出
相应给分）
(2)证明：
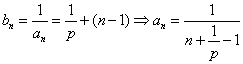8分
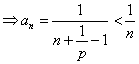10分
11分
12分
14分