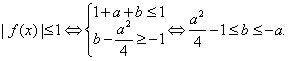新课标人教版必修5高中数学 第3章 不等式单元检测试卷
1.设![]() ,
,![]() ,则下列不等式中一定成立的是 ( )
,则下列不等式中一定成立的是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2. “![]() ”是“
”是“![]() ”的 ( )
”的 ( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
3.不等式![]() 的解集不可能是 ( )
的解集不可能是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.不等式![]() 的解集是
的解集是![]() ,则
,则![]() 的值等于 ( )
的值等于 ( )
A.-14
B.
5.不等式![]() 的解集是 ( )
的解集是 ( )
A.![]() B.
B.![]()
C.![]() 或
或![]() D.
D.![]()
6.若![]() ,则下列结论不正确的是 ( )
,则下列结论不正确的是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.若![]() ,
,![]() ,则
,则![]() 与
与![]() 的大小关系为 ( )
的大小关系为 ( )
A.![]() B.
B.![]() C.
C.![]() D.随x值变化而变化
D.随x值变化而变化
8.下列各式中最小值是2的是 ( )
A.![]() +
+![]() B.
B.![]() C.tanx+cotx D.
C.tanx+cotx D. ![]()
9.下列各组不等式中,同解的一组是 ( )
A.![]() 与
与![]() B.
B.![]() 与
与![]()
C.![]() 与
与![]() D.
D.![]() 与
与![]()
10.如果![]() 对任意实数x总成立,则a的取值范围是 ( )
对任意实数x总成立,则a的取值范围是 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
11.若![]() ,则
,则![]() 与
与![]() 的大小关系是
.
的大小关系是
.
12.函数![]() 的定义域是
.
的定义域是
.
13.某公司一年购买某种货物400吨,每次都购买![]() 吨,运费为4万元/次,一年的总存储费用为
吨,运费为4万元/次,一年的总存储费用为![]() 万元,要使一年的总运费与总存储费用之和最小,则
万元,要使一年的总运费与总存储费用之和最小,则![]() 吨.
吨.
14. 已知![]() , 则不等式
, 则不等式![]() 的解集___ _ ____.
的解集___ _ ____.
15.已知![]() 是奇函数,且在(-
是奇函数,且在(-![]() ,0)上是增函数,
,0)上是增函数,![]() ,则不等式
,则不等式![]() 的解集是___ _ ____.
的解集是___ _ ____.
16.解不等式:![]()
17.已知![]() ,解关于
,解关于![]() 的不等式
的不等式![]() .
.
18.已知![]() ,求证:
,求证:![]() 。
。
19.对任意![]() ,函数
,函数![]() 的值恒大于零,求
的值恒大于零,求![]() 的取值范围。
的取值范围。
20.如图所示,校园内计划修建一个矩形花坛并在花坛内装置两个相同的喷水器。已知喷水器的喷水区域是半径为
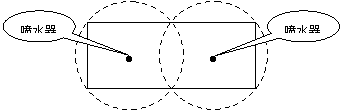 |
21.已知函数![]() .
.
(1)若对任意的实数![]() ,都有
,都有![]() ,求
,求![]() 的取值范围;
的取值范围;
(2)当![]() 时,
时,![]() 的最大值为M,求证:
的最大值为M,求证:![]() ;
;
(3)若![]() ,求证:对于任意的
,求证:对于任意的![]() ,
,![]() 的充要条件是
的充要条件是![]()
§3.5不等式单元测试
1.C; 2.A; 3.D; 4.C; 5.C; 6.D; 7.A;
8.D; 9.B; 10.A;11. ![]() ; 12.
; 12.![]() ; 13. 20 ; 14.
; 13. 20 ; 14. ![]() ;15.
;15.![]() ;
;
16.解:原不等式等价于:
![]()
![]() 或
或![]()
∴原不等式的解集为![]()
17.解:不等式![]() 可化为
可化为![]() .
.
∵![]() ,∴
,∴![]() ,则原不等式可化为
,则原不等式可化为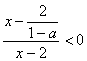 ,
,
故当![]() 时,原不等式的解集为
时,原不等式的解集为![]() ;
;
当![]() 时,原不等式的解集为
时,原不等式的解集为![]() ;
;
当![]() 时,原不等式的解集为
时,原不等式的解集为![]() .
.
18.证明:法一(综合法)
![]() ,
,
![]()
展开并移项得:![]()
![]()
法二(分析法)
要证![]() ,
,![]() ,故只要证
,故只要证![]()
即证![]() ,
,
也就是证![]() ,
,
而此式显然成立,由于以上相应各步均可逆,∴原不等式成立。
法三:![]() ,
,![]()
![]()
![]()
法四:![]()
![]() ,
,![]()
∴由三式相加得:![]()
两边同时加上![]() 得:
得:![]()
![]() ,
∴
,
∴![]()
19.解:设![]() ,
,
则![]() 的图象为一直线,在
的图象为一直线,在![]() 上恒大于0,故有
上恒大于0,故有
![]() ,即
,即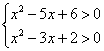 ,解得:
,解得:![]() 或
或![]()
∴![]() 的取值范围是
的取值范围是![]()
20.解:设花坛的长、宽分别为xm,ym,根据要求,矩形花坛应在喷水区域内,顶点应恰好位于喷水区域的边界。依题意得:![]() ,(
,(![]() )
)
问题转化为在![]() ,
,![]() 的条件下,求
的条件下,求![]() 的最大值。
的最大值。
法一:![]() ,
,
由![]() 和
和![]() 及
及![]() 得:
得:![]()
![]()
法二:∵![]() ,
,![]() ,
,
![]() =
=![]()
∴当![]() ,即
,即![]() ,
,![]()
由![]() 可解得:
可解得:![]() 。
。
答:花坛的长为![]() ,宽为
,宽为![]() ,两喷水器位于矩形分成的两个正方形的中心,则符合要求。
,两喷水器位于矩形分成的两个正方形的中心,则符合要求。
21. 解:(1)对任意的![]() ,都有
,都有![]()
对任意的![]() ,
,![]()
![]()
![]() ∴
∴![]() .
.
(2)证明:∵![]()
![]() ∴
∴![]() ,即
,即![]() 。
。
(3)证明:由![]() 得,
得,![]() ∴
∴![]() 在
在![]() 上是减函数,在
上是减函数,在![]() 上是增函数。
上是增函数。
∴当![]() 时,
时,![]() 在
在![]() 时取得最小值
时取得最小值![]() ,在
,在![]() 时取得最大值
时取得最大值![]() .
.
故对任意的![]() ,
,