高二数学第一学期期末模拟卷(一)
一.填空题:本大题共14小题,每小题5分,共70分.
1.抛物线![]() 的焦点坐标是
.
的焦点坐标是
.
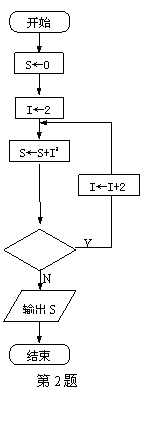
2.下面的流程图判断框中应填入 ,可以计算![]() .
.
3.命题“![]() ”的否定是
.
”的否定是
.
4.“a>
| x | 0 | 1 | 2 | 3 |
| y | 1 | 3 | 5 | 7 |
5. 已知变量![]() 与变量y之间的一组数据如表,则y与
与变量y之间的一组数据如表,则y与![]() 的线性回归方程y=b
的线性回归方程y=b![]() +
+![]() 必过点
.
必过点
.
6.甲、乙两个总体各抽取一个样本,若甲样本均值为15,乙样本均值为17,甲样本方差为3,乙样本方差为2,则总体 (填写“甲”或“乙”)波动小.
7.如果质点![]() 的位移
的位移![]() 与时间
与时间![]() 满足方程
满足方程![]() (位移单位:米,时间单位:秒),则质点在
(位移单位:米,时间单位:秒),则质点在![]() 时的瞬时速度为
米/秒.
时的瞬时速度为
米/秒.
8.从[0,1]之间选出两个数,这两个数的平方和大于1的概率是 .
9. 设函数![]() ,集合M=
,集合M=![]() ,P=
,P=![]() ,若M
,若M![]() P,则实数a的取值范围是
.
P,则实数a的取值范围是
.
10.已知一纸箱内装有某种矿泉水12瓶,其中有2瓶不合格,若质检人员从该纸箱内随机抽出2瓶,则检测到不合格产品的事件概率是 .
11.中心在原点,长轴长为8,准线方程为![]() 的椭圆标准方程为 .
的椭圆标准方程为 .
12.设点P是曲线![]() 上的任意一点,则点P到直线
上的任意一点,则点P到直线![]() 距离的最小值是 .
距离的最小值是 .
13. P是双曲线![]() 的右支上一点,M、N分别是圆(x+5)2+y2=4和(x-5)2+y2=1上的点,则PM-PN的最大值为
.
的右支上一点,M、N分别是圆(x+5)2+y2=4和(x-5)2+y2=1上的点,则PM-PN的最大值为
.
14.有如下四个命题:
命题①:方程![]() 表示焦点在
表示焦点在![]() 轴上的椭圆;
轴上的椭圆;
命题②:![]() 是直线
是直线![]() 和直线
和直线![]() 互相垂直的充要条件;
互相垂直的充要条件;
命题③:方程![]() 表示离心率大于
表示离心率大于![]() 的双曲线;
的双曲线;
命题④:“全等三角形的面积相等”的否命题.
其中真命题的序号是 .(写出所有真命题的序号)
二.解答题:本大题共6小题,每小题15分,共90分.解答应写出文字说明、证明过程或演
算步骤.
15. 已知三点P(5,2)、![]() (-6,0)、
(-6,0)、![]() (6,0)。
(6,0)。
(Ⅰ)求以![]() 、
、![]() 为焦点且过点P的椭圆的标准方程;
为焦点且过点P的椭圆的标准方程;
(Ⅱ)设点P、![]() 、
、![]() 关于直线y=x的对称点分别为
关于直线y=x的对称点分别为![]() 、
、![]() 、
、![]() ,求以
,求以![]() 、
、![]() 为焦点且过点
为焦点且过点![]() 的双曲线的标准方程.
的双曲线的标准方程.
16.先后抛掷一枚形状为正方体的骰子(正方体的六个面上分别标以数字![]() ),骰子向上的点数依次为
),骰子向上的点数依次为![]() .
.
(I) 共有多少个基本事件?
(II)
设“![]() ”为事件
”为事件![]() ,求事件
,求事件![]() 发生的概率;
发生的概率;
(Ⅲ)设“![]() ” 为事件
” 为事件![]() ,求事件
,求事件![]() 发生的概率.
发生的概率.
17. 已知![]() :方程
:方程![]() 表示椭圆;
表示椭圆;![]() :抛物线
:抛物线![]()
![]() 与
与
![]() 轴无公共点,若
轴无公共点,若![]() 是真命题且
是真命题且![]() 是假命题,求实数
是假命题,求实数![]() 的取值范围.
的取值范围.
 18.如图,等腰梯形
18.如图,等腰梯形![]() 的三边
的三边![]() 分别与函数
分别与函数![]() ,
,![]() 的图象切于点
的图象切于点![]() .求梯形
.求梯形![]() 面积的最小值.
面积的最小值.
19.为了研究某高校大学新生学生的视力情况,随机地抽查了该校100名进校学生的视力情况,得到频率分布直方图,如图.已知前4组的频数从左到右依次是等比数列![]() 的前四项,后6组的频数从左到右依次是等差数列
的前四项,后6组的频数从左到右依次是等差数列![]() 的前六项.
的前六项.
(Ⅰ)求等比数列![]() 的通项公式;
的通项公式;
(Ⅱ)求等差数列![]() 的通项公式;
的通项公式;
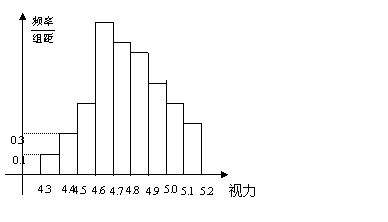 (Ⅲ)若规定视力低于5.0的学生属于近视学生,试估计该校新生的近视率
(Ⅲ)若规定视力低于5.0的学生属于近视学生,试估计该校新生的近视率![]() 的大小.
的大小.
20.设a≥0,f (x)=x-1-ln2 x+
(Ⅰ)令F(x)=xf'(x),讨论F(x)在(0.+∞)内的单调性并求极值;
(Ⅱ)求证:当x>1时,恒有x>ln2x-
高二数学试卷(一)参考答案
一.填空题:本大题共14小题,每小题5分,共70分.
1.
![]() 2. I<100 3.
2. I<100 3. ![]() 4. 充分不必要条件
4. 充分不必要条件
5.(1.5,4) 6. 乙 7. 54 8. ![]() 9. (1,+∞) 10.
9. (1,+∞) 10. ![]()
11. ![]() 12.
12. ![]() 13.
9 14.②③
13.
9 14.②③
二.解答题:本大题共6小题,每小题15分,共90分.
15. 解: (I)由题意,可设所求椭圆的标准方程为![]() +
+![]()
![]() ,其半焦距
,其半焦距![]() 。
。
![]()
![]() , ∴
, ∴![]()
![]() ,
,
![]() ,故所求椭圆的标准方程为
,故所求椭圆的标准方程为![]() +
+![]() ;
;
(II)点P(5,2)、![]() (-6,0)、
(-6,0)、![]() (6,0)关于直线y=x的对称点分别为:
(6,0)关于直线y=x的对称点分别为:
![]() 、
、![]() (0,-6)、
(0,-6)、![]() (0,6)
(0,6)
设所求双曲线的标准方程为![]() -
-![]()
![]() ,由题意知半焦距
,由题意知半焦距![]() ,
,
![]()
![]() , ∴
, ∴![]()
![]() ,
,
![]() ,故所求双曲线的标准方程为
,故所求双曲线的标准方程为![]() -
-![]() .
.
16. 解:(I) 第一次抛掷骰子有6种结果,第二次抛掷骰子也有6种结果,于是一共有:
![]() 种不同结果,因此共有36个基本事件.
种不同结果,因此共有36个基本事件.
(II)A的对立事件![]() :
:![]() ,
,
共有![]()
![]()
![]()
![]()
![]()
![]() 六种,
六种,
∴![]()
∴![]()
(或![]() ).
).
答:事件![]() 发生的概率为
发生的概率为![]() .
.
(Ⅲ)满足“![]() ”数对
”数对![]() 共有
共有![]() 五对,
五对,
∴![]() ,
,
答:事件![]() 发生的概率为
发生的概率为![]() .
.
17.解:![]() “方程
“方程![]() 表示椭圆”是真命题,
表示椭圆”是真命题,
∴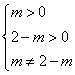
![]() ,
,
![]() “抛物线
“抛物线![]()
![]() 与
与![]() 轴无公共点”是假命题,
轴无公共点”是假命题,
∴抛物线![]()
![]() 与
与![]() 轴有公共点,
轴有公共点,
![]()
![]() ,
,
由题意得,
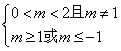
![]() .
.
18.解:解:设梯形![]() 的面积为
的面积为![]() ,点P的坐标为
,点P的坐标为![]() 。由题意得,
。由题意得,
点![]() 的坐标为
的坐标为![]() ,直线
,直线![]() 的方程为
的方程为![]() 。
。
![]()
![]()
![]()
![]() 直线
直线![]() 的方程为
的方程为![]()
即:![]()
令![]() 得,
得,![]()
令![]() 得,
得,![]()
![]()
![]()
![]()
当且仅当![]() ,即
,即![]() 时,取“=”且
时,取“=”且![]() ,
,
![]()
![]() 时,
时,![]() 有最小值为
有最小值为![]() .
.
![]() 梯形
梯形![]() 的面积的最小值为
的面积的最小值为![]()
19.解:(I)由题意知:![]() ,
,
![]()
∵数列![]() 是等比数列,
是等比数列,
∴公比![]()
∴![]() .
.
(II) ∵![]() =13,
=13,
∴![]() ,
,
∵数列![]() 是等差数列,
是等差数列,
∴设数列![]() 公差为
公差为![]() ,则得,
,则得,
![]()
∴![]() =87,
=87,
![]()
![]() ,
,![]()
![]() ,
,
![]()
![]()
(III)![]() =
=![]() ,
,
(或![]() =
=![]() )
)
答:估计该校新生近视率为91%.
20.解: (Ⅰ)根据求导法则有![]() ,
,
故![]() ,
,
于是![]() ,
,
列表如下:
|
|
| 2 |
|
|
|
| 0 |
|
|
|
| 极小值 |
|
故知![]() 在
在![]() 内是减函数,在
内是减函数,在![]() 内是增函数,所以,在
内是增函数,所以,在![]() 处取得极小值
处取得极小值![]() .
.
(Ⅱ)证明:由![]() 知,
知,![]() 的极小值
的极小值![]() .
.
于是由上表知,对一切![]() ,恒有
,恒有![]() .
.
从而当![]() 时,恒有
时,恒有![]() ,故
,故![]() 在
在![]() 内单调增加.
内单调增加.
所以当![]() 时,
时,![]() ,即
,即![]() .
.
故当![]() 时,恒有
时,恒有![]() .
.