高二数学第一学期期末模拟试卷(3)
班级 姓名 学号 成绩
考试时间：120分钟，满分：100分
可信程度表：
|
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
|
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
一、选择题：（本大题共10个小题，每小题3分，共30分.）.
[1]．某校开设
门课程供学生选修，其中
三门由于上课时间相同，至多选一门，学校规定，每位同学选修
门，则不同的选修方案种数有（ ）
A．60
B．
[2]．已知回归直线斜率的估计值为1.23，样本点的中心为（4，5），则回归直线方程为（ ）
A．
B．
C．
D．
[3]．点P与一定点F(2，0)的距离和它到一定直线x=8的距离的比是1∶2，则点P的轨迹为（ ）
A.直线 B.圆 C.椭圆 D.抛物线
[4]．已知X~N(-1,
)，若
，则
( )
[5]. 有下列四个命题:
①“
，则
”的逆命题;
②命题“a、b都是偶数，则a＋b是偶数”的逆否命题是“a＋b不是偶数，则a、b都不是偶数”;
③若有命题p：7≥7，q:ln2＞0, 则p且q是真命题;
④若一个命题的否命题为真，则它的逆命题一定是真. 其中真命题为( )
(A)①④ (B)②③ (C)②④ (D)③④
[6]．抛掷两个骰子，至少有一个4点或5点出现时，就说这些试验成功，则在10次试验中，成功次数ξ的期望是 ( )
A. 
B.
C.
D.
[7]．“x<
A.充分而不必要条件 B.必要而不充分条件 C.充要条件 D.既不充分也不必要条件
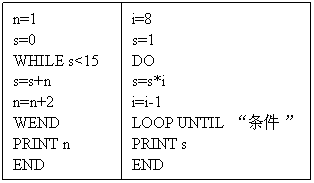[8].下列程序执行后输出的结果是（ ）
A.16
B.
[9].如果以下程序运行后输出的结果是336，那么在程序中until后面的条件应为（ ）
A. 
B.
C. 
D.
[10].
的展开式中
的系数为 （ ）
A．
B．
C．
D．
二、填空题（本大题共6个小题，每小题3分，共18分）.
[11]．设某种动物由出生算起活到10岁的概率为0.9，活到15岁的概率为0.6.现有一个10岁的这种动物，它能活到15岁的概率是
[12]．如果学生甲每次投篮投中的概率为
，那么他连续投三次，恰好两次投中的概率为_____________，至少有一次投中的概率为_____________.(用数字作答)
[13]．关于x与y，有如下数据
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
有如下的两个模型：
，
。通过残差分析发现第（1）个线性模型比第（2）个拟合效果好。则
，
（用大于，小于号填空，
是相关指数和残差平方和）
[14]．从装有
个球（其中
个白球，1个黑球）的口袋中取出
个球
,共有
种取法。在这种取法中，可以分成两类：一类是取出的个球全部为白球，一类是取出的
个白球和1个黑球，共有
，即有等式：
成立。试根据上述思想化简下列式子：
。
。
[15]．用数字1，2，3，4，5可以组成没有重复数字，并且比20000大的五位偶数共有（ ）
A.96个 B.24个 C.32个 D.36个
[16].已知
展开式中的常数项为1120 (
为常数),则展开式的各项系数和为
.
三、解答题：（本大题共5小题，共52分.解答应写出文字说明，证明过程或演算步骤.）
[17]．甲箱的产品中有5个正品和3个次品， 乙箱的产品中有4个正品和3个次品．
（Ⅰ）从甲箱中任取2个产品，求这2个产品都是次品的概率；
（Ⅱ）若从甲箱中任取2个产品放入乙箱中， 然后再从乙箱中任取一个产品，求取出的这个产品是正品的概率．
[18]．某商场经销某商品，根据以往资料统计，顾客采用的付款期数
的分布列为
|
| 1 | 2 | 3 | 4 | 5 |
|
| 0.4 | 0.2 | 0.2 | 0.1 | 0.1 |
商场经销一件该商品，采用1期付款，其利润为200元；分2期或3期付款，其利润为250元；分4期或5期付款，其利润为300元．
表示经销一件该商品的利润．
（Ⅰ）求事件
：“购买该商品的3位顾客中，至少有1位采用1期付款”的概率
；
（Ⅱ）求的分布列及期望
．
[19].为了对2006年某市中考成绩进行分析，在60分以上的全体同学中随机抽出8位，他们的数学分数(已折算为百分制)从小到大排是60、65、70、 75、80、85、 90、95，物理分数从小到大排是72、 77、 80、84、88、90、93、95.
(Ⅰ) 若规定85分(包括85分)以上为优秀，求这8位同学中恰有3位同学的数学和物理分数均为优秀的概率；
(Ⅱ) 若这8位同学的数学、物理、化学分数事实上对应如下表：
| 学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 数学分数x | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 |
| 物理分数y | 72 | 77 | 80 | 84 | 88 | 90 | 93 | 95 |
| 化学分数z | 67 | 72 | 76 | 80 | 84 | 87 | 90 | 92 |
用变量y与x、z与x的相关系数说明物理与数学、化学与数学的相关程度；
(Ⅲ) 求y与x、z与x的线性回归方程（系数精确到0.01），并用相关指数比较所求回归模型的效果.
(参考数据：
，
，
，
，
，
，
，
，
，
，
.
,
)
[20].已知+=1(a>b>0)经过点P(,－2)，离心率e=。
（1） 求椭圆的方程；
（2） 如果斜率为1的直线L经过椭圆的左焦点，且与椭圆交于A,B两点，求线段AB的长。
21.求满足a2+b2=3252的正整数a和b.要求先画出程序框图,再写出相应的程序.
[1] B
[2] C
[3] C
[4] C
[5]
[6] A
[7] A
[8] B
[9] C
[10] A
[11] 2/3
[12] 2/9;19/27
[13] ＞，＜；;
[14] 
[15] D
[16]解：设其二项式的通项为
令
，则
. 故
为常数项
令 
解得
令
则
所以展开式的各项系数和为
或
.
[17]解：（Ⅰ） 从甲箱中任取2个产品的事件数为
，
这2个产品都是次品的事件数为
．
这2个产品都是次品的概率为
．
答： 这2个产品都是次品的概率为.
（Ⅱ）设事件为“从乙箱中取一个正品”，事件
为“从甲箱中取出2个产品都是正品”，事件
为“从甲箱中取出1个正品1个次品”，事件
为“从甲箱中取出2个产品都是次品”，则事件、事件、事件彼此互斥．
．
答： 取出的这个产品是正品的概率为
．
[18]解：
（Ⅰ）由表示事件“购买该商品的3位顾客中至少有1位采用1期付款”．
知
表示事件“购买该商品的3位顾客中无人采用1期付款”
，
．
（Ⅱ）的可能取值为
元，
元，
元．
，
，
．
的分布列为
|
|
|
|
|
|
|
|
|
|
（元）．
[19]解：(Ⅰ)这8位同学中恰有3位同学的数学和物理分数均为优秀，则需要先从物理的4个优秀分数中选出3个与数学优秀分数对应，种数是
（或
），然后将剩下的5个数学分数和物理分数…………………………………4分
这8位同学的物理分数和数学分数分别对应的种数共有
。 …………5分
故所求的概率
. …………………………………………6分
(Ⅱ) 变量y与x、z与x的相关系数分别是
、
.
可以看出，物理与数学、化学与数学的成绩都是高度正相关. ……………………8分
(Ⅲ) 设y与x、z与x的线性回归方程分别是
、
.
根据所给的数据，可以计算出
，
. ……………………………10分
所以y与x和z与x的回归方程分别是
、
. …………………………………………………………11分
又y与x、z与x的相关指数是
、
. ……13分
故回归模型
比回归模型
的拟合的效果好. …14分
[20] +=1 ;AB=