高二数学第一学期期末联考模拟试卷
一、填空题（5*14=70）
1．写出下面这个命题的否定“
，
”
2．双曲线
的焦距等于
．
3．大豆栽培试验中，测得株龄
（周）与株高
（cm）的数据如下：
|
| 1 | 2 | 3 | 4 | 5 |
|
| 5 | 17 | 24 | 23 | 41 |
则对的线性回归方程为
．
4．已知命题
：
、
：
，则是的
条件．
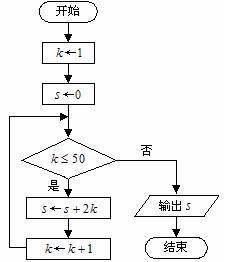5．如果执行右图的程序框图，那么输出的S等于 ．
6．某校有学生2000人，其中高三学生500人，为了了解学生的身体素质情况，采用按年级分层抽样的方法，从该校学生中抽取一个200人的样本，则样本中高三学生的人数为 ．
7．若抛物线
的焦点与椭圆
的右焦点重合，则的值为
．
8．从一堆苹果中任取了20只，并得到它们的质量（单位：克）数据分布表如下：
| 分组 |
|
|
|
|
|
|
| 频数 | 1 | 2 | 3 | 10 | 3 | 1 |
则这堆苹果中，质量不小于
9．如图，在一个边长为
，
的矩形内画一个梯形，梯形上、下底分别为
，
，高为，向该矩形内随机投一点，则所投点落在梯形内部的概率为 .
10．For x From —100 To 190 Step 10，该程序共执行循环 次.
11．函数
（
）的单调递增区间是
．
12．设
、
是椭圆
（
）的两个焦点，P为椭圆上一动点，M为P的中点，P＝4，则OM的长＝
．
13．在平面直角坐标系
中，已知△ABC的顶点A
、C
，顶点B在椭圆
上，则
．
14．已知函数
，当
时，函数
取得极大值，当
时，函数取得极小值，则
取值范围为
.
二、解答题（12+12+15+15+18+18=90）
15．设
，
，……，
（
，
）
求
，
，
，…，并由此归纳出
的表达式（不需要证明）.
16．盒子中只装有4只白球、5只黑球，从中任意取出一只球，
（1）“取出的球是黄球”是什么事件？它的概率是多少？
（2）“取出的球是白球”是什么事件？它的概率是多少？
（3）“取出的球是白球或是黑球”是什么事件，它的概率是多少？
17．对划船运动员甲、乙两人在相同的条件下进行了6次测试，测得他们最大速度的数据如下：
| 甲 | 27 | 38 | 30 | 37 | 35 | 31 |
| 乙 | 33 | 29 | 38 | 34 | 28 | 36 |
（1）作出甲、乙数据的茎叶图？（用一幅图表示）
（2）根据以上数据，试判断他们谁更优秀.
18．统计表明，某种型号的汽车在匀速行驶中每小时的耗油量（升），关于行驶速度（千米/时）的函数，解析式可以表示为
（
），已知甲、乙两地相距100千米，
（1）当汽车以
（2）当汽车以多大速度匀速行驶时，从甲地到乙地耗油最少？最少为多少升？
19．已知双曲线C的中心在原点，抛物线
的焦点是双曲线C的一个焦点，且双曲线过点
，直线
：
与双曲线C交于A、B两点，
（1）求双曲线的方程；
（2）
为何值时，
.
20．点A、B分别是椭圆
长轴的左、右端点，点F是椭圆的右焦点，点P在椭圆上，且位于轴上方，PA⊥PF，
（1）求点P的坐标；
（2）设M是椭圆长轴AB上的一点，M到直线AP的距离等于MB，求椭圆上的点到点M的距离d的最小值.
安丰高级中学高二数学期末模拟试卷答案
一 填空题
1 
2 20 3 
4 必要不充分条件 5 2550 6 50
7 4
8 70
9
10 30 11 [
，+
）
13 
14 (
,1)
二 解答题
15 解 =4x+3，=8x+7，=16x+15, …………….
16 解 （1）“取出的球是黄球”在题设条件下不可能发生，因此它是不可能事件
它的概率为0；
（2）“取出的是白球”是随机事件，它的概率为
；
（3）“取出的是白球或黑球”在题设条件下必然发生，它的概率为1。
17 解 
所以
=
，
> 
由此可以说明，甲乙两人的最大速度的平均值相同，但乙比甲更稳定，故甲优秀。
18 解 （1）当x=40千米时，汽车从甲地到乙地，行驶了
小时，要消耗汽油
。
（2）当速度为x千米/小时，汽车从甲地到乙地，行驶了
小时，设耗油量为h(x)升，依题意得
h(x)=
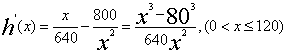
令
=0 ，解得x=80
当x
（0，80）时，因为<0,h(x)是减函数
当x（80，120）时，>0, h(x)是增函数
所以 当x=80时，因为h(x)在（0，120]上只有一个极值，所以这个极值就是最小值。
答：当汽车以
19 由题意设双曲线方程为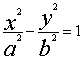
把（1，
）代入得
。。。。。。（1）
又
的焦点是（
，0）故
=与方程（1）联立，消去
可得
所以
于是
，所以双曲线的方程为
（2）由{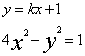
消去y得
。。。。。。。。。（2）
当
，即
且
时，直线与曲线有两个交点A，B
设A（
，
），B（
，
）
因
，故
，即
。。。。。。。。（3）
由（2）知，
代入（3）可得
+
+k+1=0
化简得 =2， 
k=
检验符合条件，故当k=时，。
20 解 （1）由已知可得点A（-6，0），F(4,0),设点P的坐标是（x,y）,则
=（x+6,y）,
.由已知得{
则消去y得
解得
.因为y>0，所以只能取
，所以
。所以点P的坐标是
（2）直线AP的方程是
设点M的坐标是（m,0）则M到直线AP的距离是
，于是=m-6,又
m6.解得m=2。椭圆上的点（x,y）到点M的距离d有
=
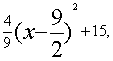
由于-6m6，所以当
时，d取得最小值
。