典型例题一
例1 甲、乙两个人独立地破译一个密码,他们能译出密码的概率分别为![]() 和
和![]() ,求:
,求:
(1)两个人都译出密码的概率;
(2)两个人都译不出密码的概率;
(3)恰有1个人译出密码的概率;
(4)至多1个人译出密码的概率;
(5)至少1个人译出密码的概率.
分析:我们把“甲独立地译出密码”记为事件![]() ,把“乙独立地译出密码”记为事件
,把“乙独立地译出密码”记为事件![]() ,显然
,显然![]() 为相互独立事件,问题(1)两个都译出密码相当于事件
为相互独立事件,问题(1)两个都译出密码相当于事件![]() 、
、![]() 同时发生,即事件
同时发生,即事件![]() .问题(2)两人都译不出密码相当于事件
.问题(2)两人都译不出密码相当于事件![]() .问题(3)恰有1个人译出密码可以分成两类:
.问题(3)恰有1个人译出密码可以分成两类:![]() 发生
发生![]() 不发生,
不发生,![]() 不发生
不发生![]() 发生,即恰有1个人译出密码相当于事件
发生,即恰有1个人译出密码相当于事件![]() .问题(4)至多1个人译出密码的对立事件是两个人都未译出密码,即事件
.问题(4)至多1个人译出密码的对立事件是两个人都未译出密码,即事件![]() .由于
.由于![]() 、
、![]() 是独立事件,上述问题中,
是独立事件,上述问题中,![]() 与
与![]() ,
,![]() 与
与![]() ,
,![]() 与
与![]() 是相互独立事件,可以用公式计算相关概率.
是相互独立事件,可以用公式计算相关概率.
解:记“甲独立地译出密码”为事件![]() ,“乙独立地译出密码”为事件
,“乙独立地译出密码”为事件![]() ,
,![]() 、
、![]() 为相互独立事件,且
为相互独立事件,且![]() .
.
(1)两个人都译出密码的概率为:
![]() .
.
(2)两个人都译不出密码的概率为:

(3)恰有1个人译出密码可以分为两类:甲译出乙未译出以及甲未译出乙译出,且两个事件为互斥事件,所以恰有1个人译出密码的概率为:

(4)“至多1个人译出密码”的对立事件为“有两个人译出密码”,所以至多1个人译出密码的概率为:
![]() .
.
(5)“至少有1个人译出密码”的对立事件为“两人未译出密码”,所以至少有1个人译出密码的概率为:
![]() .
.
说明:如果需要提高能译出密码的可能性,就需要增加可能译出密码的人,现在可以提出这样的问题:若要达到译出密码的概率为99%,至少需要像乙这样的人多少个?我们可以假设有![]() 个像乙这样的人分别独立地破译密码,此问题相当于
个像乙这样的人分别独立地破译密码,此问题相当于![]() 次独立重复试验,要译出密码相当于至少有1个译出密码,其对立事件为所有人都未译出密码,能译出密码的概率为
次独立重复试验,要译出密码相当于至少有1个译出密码,其对立事件为所有人都未译出密码,能译出密码的概率为![]() ,按要求,
,按要求,![]() ,故
,故![]() ,可以计算出
,可以计算出![]() ,即至少有像乙这样的人16名,才能使译出密码的概率达到99%.
,即至少有像乙这样的人16名,才能使译出密码的概率达到99%.
典型例题二
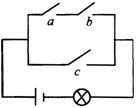 例2 如图,开关电路中,某段时间内,开关
例2 如图,开关电路中,某段时间内,开关![]() 开或关的概率均为
开或关的概率均为![]() ,且是相互独立的,求这段时间内灯亮的概率.
,且是相互独立的,求这段时间内灯亮的概率.
分析:我们把“开关![]() 合上”记为事件
合上”记为事件![]() ,“开关
,“开关![]() 合上”记为事件
合上”记为事件![]() ,“开关
,“开关![]() 合上”记为事件C,
合上”记为事件C,![]() 是相互独立事件且由已知,它们的概率都是
是相互独立事件且由已知,它们的概率都是![]() ,由物理学知识,要求灯亮,有两种可能性,一个是
,由物理学知识,要求灯亮,有两种可能性,一个是![]() 、
、![]() 两开关合上,即事件
两开关合上,即事件![]()
![]() 发生,另一个是
发生,另一个是![]() 开关合上,即事件
开关合上,即事件![]() 发生,也就是灯亮相当于事件
发生,也就是灯亮相当于事件![]() 发生.
发生.
解:分别记“开关![]() 合上”、“开关
合上”、“开关![]() 合上”、“开关
合上”、“开关![]() 合上”为事件
合上”为事件![]() ,由已知,
,由已知,![]() 是相互独立事件且概率都是
是相互独立事件且概率都是![]() .
.
开关![]() 、
、![]() 合上或开关
合上或开关![]() 合上时灯亮,所以这段时间内灯亮的概率为:
合上时灯亮,所以这段时间内灯亮的概率为:
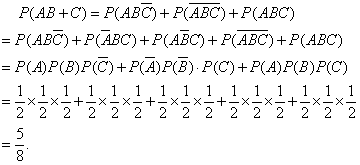
说明:本题的解题过程中,灵活使用了概率中的一些符号,比如,![]() 表示事件
表示事件![]() 与事件
与事件![]() 同时发生,
同时发生,![]() 表示事件
表示事件![]() 与事件
与事件![]() 至少有一个发生,
至少有一个发生,![]() 表示
表示![]() 与
与![]() 至少有一个发生,所以分成了三个互斥事件:
至少有一个发生,所以分成了三个互斥事件:![]() 发生
发生![]() 不发生,
不发生,![]() 不发生
不发生![]() 发生,
发生,![]() 与
与![]() 都发生,而其中
都发生,而其中![]() 不发生
不发生![]() 发生即
发生即![]() ,又
,又![]() 不发生即
不发生即![]() 与
与![]() 至少有一个不发生,从而
至少有一个不发生,从而![]() 又分成了三个互斥事件:
又分成了三个互斥事件:![]() 、
、![]() 、
、![]() ,符号语言的正确理解与使用,不仅是提高数学能力的需要,而且也使数学解题过程简便明了,一些数学结论表述更加方便.我们可以尝试理解并领会下列结论:
,符号语言的正确理解与使用,不仅是提高数学能力的需要,而且也使数学解题过程简便明了,一些数学结论表述更加方便.我们可以尝试理解并领会下列结论:
![]() .
.
典型例题三
例3 掷三颗骰子,试求:
(1)没有一颗骰子出现1点或6点的概率;
(2)恰好有一颗骰子出现1点或6点的概率.
分析:我们把三颗骰子出现1点或6点分别记为事件![]() ,由已知,
,由已知,![]() 是相互独立事件.问题(1)没有1颗骰子出现1点或6点相当于
是相互独立事件.问题(1)没有1颗骰子出现1点或6点相当于![]() ,问题(2)恰有一颗骰子出现1点或6点可分为三类:
,问题(2)恰有一颗骰子出现1点或6点可分为三类:![]() ,三个事件为互斥事件.问题(1)可以用相互独立事件的概率公式求解,问题(2)可以用互斥事件的概率公式求解.
,三个事件为互斥事件.问题(1)可以用相互独立事件的概率公式求解,问题(2)可以用互斥事件的概率公式求解.
解:记“第1颗骰子出现1点或6点”为事件![]() ,由已知
,由已知![]() 是相互独立事件,且
是相互独立事件,且![]() .
.
(1)没有1颗骰子出现1点或6点,也就是事件![]() 全不发生,即事件
全不发生,即事件![]() ,所以所求概率为:
,所以所求概率为:
![]() .
.
(2)恰好有1颗骰子出现1点或6点,即![]() 发生
发生![]() 不发生
不发生![]() 不发生或
不发生或![]() 不发生
不发生![]() 发生
发生![]() 不发生或
不发生或![]() 不发生
不发生![]() 不发生
不发生![]() 发生,用符号表示为事件
发生,用符号表示为事件![]() ,所求概率为:
,所求概率为:
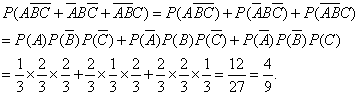
说明:再加上问题:至少有1颗骰子出现1点或6点的概率是多少?我们逆向思考,其对立事件为“没有一颗骰子出现1点或6点,即问题(1)中的事件,所求概率为![]() ,在日常生活中,经常遇到几个独立事件,要求出至少有一个发生的概率,比如例1中的至少有1个人译出密码的概率,再比如:有两门高射炮,每一门炮击中飞机的概率都是0.6,求同时发射一发炮弹,击中飞机的概率是多少?把两门炮弹击中飞机分别记为事件A与B,击中飞机即 A与B至少有1个发生,所求概率为
,在日常生活中,经常遇到几个独立事件,要求出至少有一个发生的概率,比如例1中的至少有1个人译出密码的概率,再比如:有两门高射炮,每一门炮击中飞机的概率都是0.6,求同时发射一发炮弹,击中飞机的概率是多少?把两门炮弹击中飞机分别记为事件A与B,击中飞机即 A与B至少有1个发生,所求概率为![]() .
.
典型例题四
例4 某工厂的产品要同时经过两名检验员检验合格方能出厂,但在检验时也可能出现差错,将合格产品不能通过检验或将不合格产品通过检验,对于两名检验员,合格品不能通过检验的概率分别为![]() ,不合格产品通过检验的概率分别为
,不合格产品通过检验的概率分别为![]() ,两名检验员的工作独立.求:(1)一件合格品不能出厂的概率,(2)一件不合格产品能出厂的概率.
,两名检验员的工作独立.求:(1)一件合格品不能出厂的概率,(2)一件不合格产品能出厂的概率.
分析:记“一件合格品通过两名检验员检验”分别记为事件![]() 和事件
和事件![]() ,问题(1)一件合格品不能出厂相当于一件合格品至少不能通过一个检验员检验,逆向考虑,其对立事件为合格品通过两名检验,即
,问题(1)一件合格品不能出厂相当于一件合格品至少不能通过一个检验员检验,逆向考虑,其对立事件为合格品通过两名检验,即![]() 发生,而
发生,而![]() 的概率可以用相互独立事件的概率公式求解.我们把“一件不合格品通过两名检验员检验”分别记为事件
的概率可以用相互独立事件的概率公式求解.我们把“一件不合格品通过两名检验员检验”分别记为事件![]() 和事件
和事件![]() ,则问题(2)一件不合格品能出厂相当于一件不合格品同时通过两名检验员检验,即事件
,则问题(2)一件不合格品能出厂相当于一件不合格品同时通过两名检验员检验,即事件![]() 发生,其概率可用相互独立事件概率公式求解.
发生,其概率可用相互独立事件概率公式求解.
解:(1)记“一件合格品通过第i名检验员检验”为事件![]() ,“一件合格品不能通过检验出厂”的对立事件为“一件合格品同时通过两名检验员检验”,即事件
,“一件合格品不能通过检验出厂”的对立事件为“一件合格品同时通过两名检验员检验”,即事件![]() 发生.
发生.
所以所求概率为![]()
![]() .
.
(2)“一件不合格品能通过第i名检验员检验”记为事件![]() ,“一件不合格品能出厂”即不合格品通过两名检验员检验,事件
,“一件不合格品能出厂”即不合格品通过两名检验员检验,事件![]() 发生,所求概率为:
发生,所求概率为:
![]() .
.
典型例题五
例5
某大学的校乒乓球队与数学系乒乓球队举行对抗赛,校队的实力比系队强,当一个校队队员与系队队员比赛时,校队队员获胜的概率为0.6.现在校、系双方商量对抗赛的方式,提出了三种方案:(1)双方各出3人;(2)双方各出5人;(3)双方各出7人.三种方案中场次比赛中得胜人数多的一方为胜利.问:对系队来说,哪一种方案最有利?三种方案中,哪一种方案系队获胜的概率更大一些,哪一种方案对系队更有利.进行几场比赛相当于进行几次独立重复试验,可以用n次独立重复试验中某事件发生![]() 次的概率方式解题.
次的概率方式解题.
解:记一场比赛系队获胜为事件![]() ,事件
,事件![]() 的对立事件为校队获胜,所以
的对立事件为校队获胜,所以![]()
用方案(1),![]() 发生两次为系队胜,
发生两次为系队胜,![]() 发生3次也为系队胜,所以系队胜的概率为:
发生3次也为系队胜,所以系队胜的概率为:
![]()
用方案(2),![]() 发生3、4、5次为系队胜.
发生3、4、5次为系队胜.
所以系队胜的概率为:
![]()
用方案(3),![]() 发生4、5、6、7次为系队胜.
发生4、5、6、7次为系队胜.
所以系队胜的概率为:
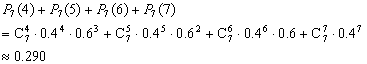
比较可以看出,双方各出3个人对系队更有利,获胜概率为0.352.
实际上,对弱队而言,比赛场数越少,对弱队越有利,侥幸取胜的可能性越大.
说明:在日常生活中,经常出现方案的比较问题,或者方案是否合理的论证问题,比如产品抽查,抽检几件比较合理,因为抽多了浪费人力,抽少了容易让不合格产品出厂.设备维修安排几位维修工较合理,安排人员过多造成浪费,安排人员过少设备不能及时维修,这些问题都可以用本题的思维方法,先设计一个独立重复试验,然后抓某个事件发生的概率,看概率是否较小.
我们可以看例子:10台同样的设备,各自独立工作,设备发生故障的概率为0.01,现在安排1名维修工,试说明这种配备是否合理?10台设备各自独立工作,相当于10次独立重复试验,有1名维修工人,若两台以上机器发生故障则得不到及时维修,其对立事件为至多1台机器发生故障,我们可以得到多于1台机器发生故障的概率为:
![]() .
.
从结果来看,得不到及时维修的概率很小,安排一人维修比较合理.
典型例题六
例6 判断下列各对事件是否是相互独立事件
(1)甲组3名男生、2名女生;乙组2名男生、3名女生,今从甲、乙两组中各选1名同学参加演讲比赛,“从甲组中选出1名男生”与“从乙组中选出1名女生”.
(2)容器内盛有5个白乒乓球和3个黄乒乓球,“从8个球中任意取出1个,取出的是白球”与“从剩下的7个球中任意取出1个,取出的还是白球”.
(3)一筐内有6个苹果和3个梨,“从中任意取出1个,取出的是苹果”与“把取出的苹果放回筐子,再从筐子中任意取出1个,取出的是梨”.
分析:两事件是否相互独立,就是要看其中一个事件发生与否对另一事件发生的概率是否有影响.
解:(1)“从甲组选出1名男生”这一事件是否发生,对“从乙组选出1名女生”这一事件发生的概率没有影响,所以它们是相互独立事件.
(2)“从8个球中任意取出1个,取出的是白球”的概率为![]() ,若这一事件发生了,则“从剩下的7个球中任意取出1个,取出的仍是白球”的概率为
,若这一事件发生了,则“从剩下的7个球中任意取出1个,取出的仍是白球”的概率为![]() ;若前一事件没有发生,则后一事件发生的概率为
;若前一事件没有发生,则后一事件发生的概率为![]() .可见,前一事件是否发生,对后一事件发生的概率有影响,所以二者不是相互独立事件.
.可见,前一事件是否发生,对后一事件发生的概率有影响,所以二者不是相互独立事件.
(3)由于把取出的苹果又放回筐子,故对“从中任意取出1个,取出的是梨”的概率没有影响.所以二者是相互独立事件.
说明:要明确相互独立事件(1)对两个事件而言的,(2)其中一个事件的发生与否对另一个事件发生的概率没有影响.
典型例题七
例7 判断下列各对事件是互斥事件还是相互独立事件.
(1)运动员甲射击1次,“射中9环”与“射中8环”;
(2)甲、乙二运动员各射击1次,“甲射中10环”与“乙射中9环”;
(3)甲、乙二运动员各射击1次,“甲、乙都射中目标”与“甲、乙都没有射中目标”;
(4)甲、乙二运动员各射击1次,“至少有1人射中目标”与“甲射中目标,但乙没有射中目标”.
解:甲射击1次,“射中9环”与“射中8环”两个事件不可能同时发生,二者是互斥事件.
(2)甲、乙各射击1次,“甲射中10环”发生与否,对“乙射中9环”的概率没有影响,二者是相互独立事件.
(3)甲、乙各射击1次,“甲、乙都射中目标”与“甲、乙都没有射中目标”不可能同时发生,二者是互斥事件.
(4)甲、乙各射击1次,“至少有1人射中目标”与“甲射中目标,但乙没有射中目标”可能会同时发生,二者构不成互斥事件,也不可能是相互独立事件.
说明:上一节学习的“互斥事件”与本节学习的“独立事件”是不同的两个概念.
它们的相同点都是对两个事件而言的.
它们的不同点是:“互斥事件”是说两个事件不能同时发生;“相互独立事件”是说一个事件发生与否对另一个事件发生的概率没有影响.
这两个概念一定要搞清楚,今后解题量常须区分这两个概念.
典型例题八
例8 一批产品共有![]() 个,其中
个,其中![]() 个是次品.从这批产品中任意抽取1个来检查;记录其等级后,再放回去,如此连续抽查
个是次品.从这批产品中任意抽取1个来检查;记录其等级后,再放回去,如此连续抽查![]() 次.求
次.求![]() 次都取得合格品的概率.
次都取得合格品的概率.
分析:要明确“![]() 次都取得合格品”的事件,是指“第一次取得合格品”到“第
次都取得合格品”的事件,是指“第一次取得合格品”到“第![]() 次取得合格品”这
次取得合格品”这![]() 个事件同时发生的事件.因此需要求“
个事件同时发生的事件.因此需要求“![]() 次都取得合格品”的概率,这样就要看这
次都取得合格品”的概率,这样就要看这![]() 个事件是否相互独立.因为抽取的产品在检验后都要放回去,所以“前次取得合格品”的事件是否发生,对“后次取得合格品”的概率没有影响,可知它们是相互独立的事件.
个事件是否相互独立.因为抽取的产品在检验后都要放回去,所以“前次取得合格品”的事件是否发生,对“后次取得合格品”的概率没有影响,可知它们是相互独立的事件.
解:设![]() ,
,![]() ,…,
,…,![]() 诸事件分别表示第1次,第2次,…,第
诸事件分别表示第1次,第2次,…,第![]() 次抽查时取得的合格品.由分析可知
次抽查时取得的合格品.由分析可知![]() ,
,![]() ,…,
,…,![]() 是相互独立事件,可得
是相互独立事件,可得![]() ,
,
其中![]()
∴![]()
![]() .
.
![]()
可得![]() 次都取得合格品的概率为
次都取得合格品的概率为![]()
说明:当![]() ,
,![]() ,…,
,…,![]() 这
这![]() 个事件相互独立时,才能应用公式
个事件相互独立时,才能应用公式
![]() .
.
典型例题九
例9 甲、乙二射击运动员分别对一目标射击1次,甲射中的概率为![]() ,乙射中的概率为
,乙射中的概率为![]() ,求:
,求:
(1)2人都射中的概率?
(2)2人中有1人射中的概率?
(3)2人至少有1人射中的概率?
(4)2人至多有1人射中的概率?
分析:设“甲射击1次,击中目标”为事件![]() ,“乙射击1次,击中目标”为事件
,“乙射击1次,击中目标”为事件![]() ,则
,则![]() 与
与![]() ,
,![]() 与
与![]() ,
,![]() 与
与![]() ,
,![]() 与
与![]() 为相互独立事件.
为相互独立事件.
解:(1) 2人都射中的概率为
![]() .
.
(2) 2人中恰有1人射中包括甲中乙不中、甲不中乙中2种情况,其对应事件为互斥事件:
![]()
![]()
![]() .
.
(3)解法1:2人至少有1人射中包括“2人都射中”和“2人有1人不中”2种情况,其概率为:
![]()
![]()
解法2:“2人至少有1人击中”与“2人都未击中”为对立事件.
所以“2人至少有1人击中”的概率为![]() .
.
(4)解法1:“至多有1人击中目标”包括“有1人击中”和“2人都未击中”,故所求概率为
![]()
![]()
![]()
解法2:“至多有1人击中目标”的对立事件是“2人都击中目标”,故所求概率为:
![]() .
.
典型例题十
例10 射击运动员李强射击一次击中目标的概率是![]() ,他射击3次,恰好2次击中目标的概率是多少?
,他射击3次,恰好2次击中目标的概率是多少?
分析1:看成相互独立事件.设第1,2,3次射击中,射手击中目标的事件分别为![]() ,
,![]() ,
,![]() ,未击中目标的事件分别为
,未击中目标的事件分别为![]() ,
,![]() ,
,![]() ,射击3次,恰好2次击中目标可有下面几种情况.
,射击3次,恰好2次击中目标可有下面几种情况.
![]() ,
,![]() ,
,![]() .
.
每种情况,都可看成在3个位置上取2个写上![]() ,另1个写上
,另1个写上![]() ,这些情况的种数等于从3个元素中取出2个组合数
,这些情况的种数等于从3个元素中取出2个组合数![]() .
.
各次射击是否击中目标相互之间独立,根据相互独立事件的概率乘法公式,前2次击中目标,第3次未击中目标的概率
![]()
![]()
![]()
同理,![]() ,
,![]() .
.
解法1:由分析可知射击3次,恰好2次击中目标的3种情况中,每一种情况发生的概率都是![]() .由于3种情况彼此互斥,根据互斥事件的概率加法公式,射击3次,恰好2次击中目标的概率为
.由于3种情况彼此互斥,根据互斥事件的概率加法公式,射击3次,恰好2次击中目标的概率为
![]()
![]()
![]() .
.
分析2:看成独立重复试验.
解法2:射手射击一次击中目标的概率为![]() ,他射击3次恰好2次击中目标的概率为
,他射击3次恰好2次击中目标的概率为
![]()
说明:![]() 是
是![]() 次独立重复试验中某事件
次独立重复试验中某事件![]() 恰好发生
恰好发生![]() 次的概率.
次的概率.![]() 是重复试验的次数,
是重复试验的次数,![]() 是在1次试验中某事件
是在1次试验中某事件![]() 发生的概率,
发生的概率,![]() 是在
是在![]() 次独立试验中事件
次独立试验中事件![]() 恰好发生的次数.弄清公式中
恰好发生的次数.弄清公式中![]() 、
、![]() 、
、![]() 这些量的意义,才能正确运用这一公式求解
这些量的意义,才能正确运用这一公式求解![]() 次独立重复试验中事件
次独立重复试验中事件![]() 恰好发生
恰好发生![]() 次的概率.
次的概率.
典型例题十一
例11 在一次考试中出了六道是非题,正确的记“√”号,不正确的记“×”号.若某考生完全记上六个符号,试求:
(1)全部是正确的概率;
(2)正确解答不少于4道的概率;
(3)至少正确解答一半的概率.
分析:由已知可知每个题解答正确的概率为![]() ,并且每次解答是相互独立事件.
,并且每次解答是相互独立事件.
解:(1)全部正确的概率是![]() .
.
(2)“正确解答不少于4道”即“有4道题、5道题或6道题正确”,故所求概率为
![]()
![]()
![]() .
.
(3)“至少正确解答一半”即“有3道题或3道以上正确”,故所求概率为
![]()
![]()
![]() .
.
说明:独立重复试验是同一试验的![]() 次重复.每次试验结果的概率不受其它次结果的概率的影响,每次试验有两个可能结果:成功或失败.
次重复.每次试验结果的概率不受其它次结果的概率的影响,每次试验有两个可能结果:成功或失败.![]() 次试验中
次试验中![]() 恰好出现了
恰好出现了![]() 次的概率为
次的概率为![]() ,这
,这![]() 次是
次是![]() 次中的任意
次中的任意![]() 次.
次.
典型例题十二
例12 纺织厂某车间内有三台机器,这三台机器在一天内不需工人维护的概率:第一台为![]() ,第二台为
,第二台为![]() ,第三台为
,第三台为![]() ,问一天内:
,问一天内:
(1)![]() 台机器都要维护的概率是多少?
台机器都要维护的概率是多少?
(2)其中恰有一台要维护的概率是多少?
(3)至少一台需要维护的概率是多少?
分析:三台机器是否需要维护,相互之间是没有影响的,故可用概率的乘法公式;“至少”问题可以反面考虑.
解:(1)记一天内三台机器需要维护的事件分别为![]() .易见
.易见![]() 相互独立.又一天内三台机器都要维护就是事件
相互独立.又一天内三台机器都要维护就是事件![]() ,上概率乘法公式有
,上概率乘法公式有
![]()
![]()
![]() .
.
答:三台机器都要维护的概率是![]() .
.
(2)一天内恰有一台机器需要维护有三种情况:事件![]() 发生,或事件
发生,或事件![]() 发生,或事件
发生,或事件![]() 发生,这三种情况不可能同时发生,故互斥,因此有
发生,这三种情况不可能同时发生,故互斥,因此有
![]()
![]()
![]()
答:恰有一台机器需要维护的概率为![]() .
.
(3)从反面考虑:一天内三台机器都不需维护的概率为
![]()
![]() .
.
因此,至少有一台需要维护的概率为
![]()
![]() .
.
答:至少有一台需要维护的概率为![]() .
.
说明:注意判断事件间的互斥性和独立性,从而利用概率的加法或乘法公式.事件的正、反两方面都要考虑全面.
典型例题十三
例13 设每支步枪射击飞机命中率为![]() ,现用
,现用![]() 支步枪同时独立进行一次射击,求击中飞机的概率是多少?若要以
支步枪同时独立进行一次射击,求击中飞机的概率是多少?若要以![]() 的概率击中一架飞机,需要有多少支步枪同时射击?
的概率击中一架飞机,需要有多少支步枪同时射击?
分析:容易看出,该题应用逆向思维,从反而考虑.
解:(1) ![]() 支步枪都未击中飞机的概率为:
支步枪都未击中飞机的概率为:
![]() .
.
∴![]()
设需![]() 支步枪同时射击,则有
支步枪同时射击,则有
![]() ,
,
∴![]() .
.
取对数![]() ,
,
∴![]() (支).
(支).
答:用![]() 支步枪进行一次射击,击中飞机的概率为
支步枪进行一次射击,击中飞机的概率为![]() ;欲以
;欲以![]() 的概率击中飞机,需用
的概率击中飞机,需用![]() 支步枪同时射击.
支步枪同时射击.
说明:射击命中率问题是很典型的一类实际问题.它一般要涉及到概率乘法公式、反面间接解决、![]() 次独立重复试验中某事件恰发生
次独立重复试验中某事件恰发生![]() 次的概率公式等.应熟练掌握这类问题的解法.
次的概率公式等.应熟练掌握这类问题的解法.
典型例题十四
例14 我舰用鱼雷打击来犯的敌舰,至少有![]() 枚鱼雷击中敌舰时,敌舰才被击沉.如果每枚鱼雷的命中率都是
枚鱼雷击中敌舰时,敌舰才被击沉.如果每枚鱼雷的命中率都是![]() ,当我舰上的
,当我舰上的![]() 个鱼雷发射器同是向敌舰各发射
个鱼雷发射器同是向敌舰各发射![]() 枚鱼雷后,求敌舰被击沉的概率(结果保留
枚鱼雷后,求敌舰被击沉的概率(结果保留![]() 位有效数字).
位有效数字).
分析:![]() 个发射器各发射
个发射器各发射![]() 枚鱼雷相当于作
枚鱼雷相当于作![]() 次独立重复试验.直接用公式即可.
次独立重复试验.直接用公式即可.
解:记“发射![]() 次,击中敌舰”为事件
次,击中敌舰”为事件![]() ,则至少
,则至少![]() 次击中敌舰的概率为
次击中敌舰的概率为
![]()
![]()
![]()
![]()
答:敌舰被击沉的概率为![]() .
.
说明:本章所讲的“古典概型”中,主要有![]() 种概率类型,即互斥事件有一个发生的概率、相互独立事件同时发生的概率、
种概率类型,即互斥事件有一个发生的概率、相互独立事件同时发生的概率、![]() 次独立重复试验中某事件恰发生
次独立重复试验中某事件恰发生![]() 次的概率.正确辨别概率类型是解题的关键.当然有些问题可能是几种类型的综合.本题就属于第3种类型.
次的概率.正确辨别概率类型是解题的关键.当然有些问题可能是几种类型的综合.本题就属于第3种类型.
典型例题十五
例15 假设飞机的每一台发动机在飞行中的故障率都是![]() ,且各发动机互不影响.如果至少
,且各发动机互不影响.如果至少![]() 的发动机能正常运行,飞机就可以顺利地飞行.问对于多大的
的发动机能正常运行,飞机就可以顺利地飞行.问对于多大的![]() 而言,四发动机飞机比二发动机飞机更安全?
而言,四发动机飞机比二发动机飞机更安全?
分析:![]() 台发动机中要有
台发动机中要有![]() 台(或
台(或![]() 、
、![]() 台)正常运行,而这
台)正常运行,而这![]() 台可以是任意的.故属
台可以是任意的.故属![]() 次独立重复试验问题.
次独立重复试验问题.![]() 台发动机的情形同理.建立不等式求解.
台发动机的情形同理.建立不等式求解.
解:四发动机飞机成功飞行的概率为
![]()
![]()
二发动机飞机成功飞行的概率为
![]()
要使四发动机飞机比二发动机飞机安全,只要
![]()
化简整理,解得![]() .
.
答:当发动机不出故障的概率大于![]() 时,四发动机飞机比二发动机飞机安全.
时,四发动机飞机比二发动机飞机安全.
说明:(1)计算飞机成功飞行的概率时可从反面考虑:四发动机为![]() ,二发动机为
,二发动机为![]() ,这样更简单.(2)该题并不是直接求事件发生的概率,而是已知概率(关系)求其他量,其实要考查的知识、方法还是一样.万变不离其宗.解题时应适应这种变化.
,这样更简单.(2)该题并不是直接求事件发生的概率,而是已知概率(关系)求其他量,其实要考查的知识、方法还是一样.万变不离其宗.解题时应适应这种变化.
典型例题十六
例16 猎人在距离![]() 处射击一只野兔,其命中率为
处射击一只野兔,其命中率为![]() .如果第一次射击未命中,则猎人进行第二次射击,但距离为
.如果第一次射击未命中,则猎人进行第二次射击,但距离为![]() ;如果第二次又未命中,则猎人进行第三次射击,但在射击瞬间距离野兔为
;如果第二次又未命中,则猎人进行第三次射击,但在射击瞬间距离野兔为![]() .已知猎人命中率与距离的平方成反比,求猎人命中野兔的概率.
.已知猎人命中率与距离的平方成反比,求猎人命中野兔的概率.
分析:各次射击是相互独立事件,各次“射中”是互斥事件.先求出各次“射中”的概率,再相加即可.
解:记三次射击“射中”分别为![]() 、
、![]() 、
、![]() .其中
.其中![]() .又由题意有
.又由题意有
![]() ,∴
,∴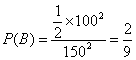
![]() ,∴
,∴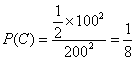 .
.
∴命中野兔的概率为
![]()
![]()
![]()
![]() .
.
答:猎人命中野兔的概率为![]() .
.
说明:注意分析整个事件的结构.总的来说,各次射击中“击中”事件是互斥的,因为只需击中一次即可,“击中”两次或三次不会同时发生.但每次射击又是独立的.因此,“击中野兔”这个事可分解为三个互斥的事件之和:第一次击中;第一次未击中而第二次击中;第一次、第二次都未击中而第三次击中,即![]() .实际上这是两种概型的结合:相互独立事件同时发生的概率、互斥事件有一个发生的概率.很多综合题具有这种结构.这类似于排列组合中分步计数原理和分类计数原理结合使用的问题.
.实际上这是两种概型的结合:相互独立事件同时发生的概率、互斥事件有一个发生的概率.很多综合题具有这种结构.这类似于排列组合中分步计数原理和分类计数原理结合使用的问题.
典型例题十七
例17 如图,用![]() 三类不同的元件连接成两个系统
三类不同的元件连接成两个系统![]() ,
,![]() .当元件
.当元件![]() 都正常工作时,系统
都正常工作时,系统![]() 正常工作;当元件
正常工作;当元件![]() 正常工作且元件
正常工作且元件![]() 至少有一个正常工作时,系统
至少有一个正常工作时,系统![]() 正常工作.已知元件
正常工作.已知元件![]() 正常工作的概率依次为
正常工作的概率依次为![]() ,
,![]() ,
,![]() .分别求系统
.分别求系统![]() ,
,![]() 正常工作的概率
正常工作的概率![]() ,
,![]() .
.
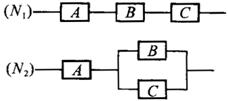
分析一:正向思考,利用独立事件同时发生的概率乘法公式计算概率.
解法一:分别记元件![]() 正常工作为事件
正常工作为事件![]() ,由已知条件得,
,由已知条件得,![]() ,
,![]() ,
,![]() .
.
(1)因为事件![]() 是相互独立的.所以,系统
是相互独立的.所以,系统![]() 正常工作的概率:
正常工作的概率:
![]()
![]()
故系统![]() 正常工作的概率为
正常工作的概率为![]() .
.
(2)系统![]() 正常工作的概率
正常工作的概率![]()
因为![]() .
.![]() .
.
所以![]() .
.
故系统![]() 正常工作的概率为
正常工作的概率为![]() .
.
分析二:逆向思考,利用对立事件概率计算公式求概率.
解法二:分别记元件![]() 正常工作为事件
正常工作为事件![]() ,元件
,元件![]() 不正常工作为事件
不正常工作为事件![]() ,
,![]() ,
,![]() ,由已知条件有:
,由已知条件有:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() .
.
(1)系统![]() 正常工作的概率
正常工作的概率
![]()
![]()
![]()
![]()
![]() .
.
(2)![]()
![]()
![]()
![]()
说明:本题为相互独立事件同时发生或互斥事件恰有一个发生的概率的计算,解题关键是正向思考用概率的乘法公式和逆向思考用对立事件概率计算公式.