(数学选修1-1)第一章 导数及其应用[综合训练B组]及答案
一、选择题
1.函数![]() 有( )
有( )
A.极大值![]() ,极小值
,极小值![]()
B.极大值![]() ,极小值
,极小值![]()
C.极大值![]() ,无极小值
,无极小值
D.极小值![]() ,无极大值
,无极大值
2.若![]() ,则
,则![]() ( )
( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
3.曲线![]() 在
在![]() 处的切线平行于直线
处的切线平行于直线![]() ,则
,则![]() 点的坐标为( )
点的坐标为( )
A.![]() B.
B.![]()
C.![]() 和
和![]() D.
D.![]() 和
和![]()
4.![]() 与
与![]() 是定义在R上的两个可导函数,若
是定义在R上的两个可导函数,若![]() ,
,![]() 满足
满足![]() ,则
,则
![]() 与
与![]() 满足( )
满足( )
A.![]()
![]() B.
B.![]()
![]() 为常数函数
为常数函数
C.![]()
![]() D.
D.![]()
![]() 为常数函数
为常数函数
5.函数![]() 单调递增区间是( )
单调递增区间是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.函数![]() 的最大值为( )
的最大值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题
1.函数![]() 在区间
在区间![]() 上的最大值是 。
上的最大值是 。
2.函数![]() 的图像在
的图像在![]() 处的切线在x轴上的截距为________________。
处的切线在x轴上的截距为________________。
3.函数![]() 的单调增区间为
,单调减区间为___________________。
的单调增区间为
,单调减区间为___________________。
4.若![]() 在
在![]() 增函数,则
增函数,则![]() 的关系式为是
。
的关系式为是
。
5.函数![]() 在
在![]() 时有极值
时有极值![]() ,那么
,那么![]() 的值分别为________。
的值分别为________。
三、解答题
1. 已知曲线![]() 与
与![]() 在
在![]() 处的切线互相垂直,求
处的切线互相垂直,求![]() 的值。
的值。
 |
2.如图,一矩形铁皮的长为
四个相同的小正方形,制成一个无盖的小盒子,问小正方形的边长
为多少时,盒子容积最大?
3. 已知![]() 的图象经过点
的图象经过点![]() ,且在
,且在![]() 处的切线方程是
处的切线方程是![]()
(1)求![]() 的解析式;(2)求
的解析式;(2)求![]() 的单调递增区间。
的单调递增区间。
4.平面向量![]() ,若存在不同时为
,若存在不同时为![]() 的实数
的实数![]() 和
和![]() ,使
,使
![]() 且
且![]() ,试确定函数
,试确定函数![]() 的单调区间。
的单调区间。
(数学选修1-1)第一章 导数及其应用 [综合训练B组]
一、选择题
1.C
![]() ,当
,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]()
当![]() 时,
时,![]() ;
;![]() 取不到
取不到![]() ,无极小值
,无极小值
2.D
![]()
3.C
设切点为![]() ,
,![]() ,
,
把![]() ,代入到
,代入到![]() 得
得![]() ;把
;把![]() ,代入到
,代入到![]() 得
得![]() ,所以
,所以![]() 和
和![]()
4.B
![]() ,
,![]() 的常数项可以任意
的常数项可以任意
5.C
令![]()
6.A
令![]() ,当
,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,![]() ,在定义域内只有一个极值,所以
,在定义域内只有一个极值,所以![]()
二、填空题
1.![]()
![]() ,比较
,比较![]() 处的函数值,得
处的函数值,得![]()
2.![]()
![]()
3.![]()
![]()
![]()
4.![]()
![]() 恒成立,
恒成立,
则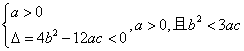
5.![]()
![]()
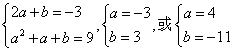 ,当
,当![]() 时,
时,![]() 不是极值点
不是极值点
三、解答题
1.解:![]()
![]() 。
。
2.解:设小正方形的边长为![]() 厘米,则盒子底面长为
厘米,则盒子底面长为![]() ,宽为
,宽为![]()
![]()
![]() ,
,![]() (舍去)
(舍去)
![]() ,在定义域内仅有一个极大值,
,在定义域内仅有一个极大值,
![]()
3.解:(1)![]() 的图象经过点
的图象经过点![]() ,则
,则![]() ,
,
![]()
切点为![]() ,则
,则![]() 的图象经过点
的图象经过点![]()
得![]()
![]()
(2)![]()
单调递增区间为![]()
4.解:由![]() 得
得![]()
![]()
![]()
![]()
![]()
所以增区间为![]() ;减区间为
;减区间为![]() 。
。