高二理科数学第一学期教学质量检测试

高二理科数学第一学期教学质量检测试

本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。满分120分，考试时间120分钟。

第I卷（选择题 共48分）

注意事项：

1．答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上。

2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑。如需改动，用橡皮擦干净后，再选涂其他答案标号。不能答在试卷上。

一、选择题：本大题共12个小题.每小题4分；共48分.在每小题给出的四个选项中，只有一个选项是符合题目要求的.

1．设复数z满足　　　　　　　　　　　　　　　　　　　　　 （　　）

　　A．－2+i　　　　　B．－2－i　　　　 C．2－i　　　　　 D．2+i

2．数学中的综合法是　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　A．由结果追溯到产生原因的思维方法　 B．由原因推导到结果的思维方法

　　C．由反例说明结果不成立的思维方法　 D．由特例推导到一般的思维方法

3．函数在（1，1）处的切线方程为　　　　　　　　　　　　　（　　）

　　A．　　B．　　 C．　　D．

4．工人甲生产的机器零件合格率为90%，工人乙生产的机器零件合格率为96%，现从他们生产的零件中各抽取1件，则此两件中只有1件是合格品的概率为　　　　（　　）

　　A．0.06　　　　　 B．0.45　　　　　 C．0.132　　　　　D．0.236

5．已知随机变量X的概率分布列如下表：则其数学期望为　　　　　　　　　　 （　　）

X	0	1	2	3	4
p	0.1	0.2	0.04	0.06	0.6

　　A．1.86　　　　　 B．2.86　　　　　 C．2.96　　　　　 D．0.46

6．某单位组织职工义务鲜血，在检验合格的人中，O型血8人，A型血7人，B型血5人，AB型血4人，现从四种血型的人中各选1人去献血，共有不同的选法　　（　　）

　　A．16种　　　　　 B．24种　　　　　 C．1680种　　　　 D．1120种

7．函数的单调区间为　　　　　　　　　　　　　　　　　（　　）

　　A．（－2，3）　　　　　　　　　　　　B．（―∞，―2）和（－2，3）

　　C．（－2，3）和（3，+∞）　　　　　　D．（－∞，－2）和（3，+∞）

8．当x，y是什么整数时，复数是纯虚数　　　 （　　）

　　A．x=3且y≠1　　　　　　　　　　　 B．x=4且y≠4，y≠－1

　　C．x=4且y≠4，y≠3　　　　　　　　 D．x=3，y=4

2,4,6

9．　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　A．0　　　　　　　B．101　　　　　　C．98　　　　　　 D．97

10．观察下列数：3，2，6，5，15，14，x，y，z，122，……中，x，y，z的值依次是（　　）

　　A．42，41，123　　B．13，39，123　　C．24，23，123　　D．28，27，123

11．已知的展开式中的第三项与第五项的系数之比为，则此展开式中的常数项为　　　　　　　　　　　　（　　）

　　A．45i　　　　　　B．－45i　　　　　C．45　　　　　　 D．－45

12．正态总体为时的概率密度函数则下列判断正确的是　　　　　　 （　　）

　　A．函数f（x）是奇函数且在（－∞，+∞）上单调递减

　　B．函数f（x）是奇函数且在（－∞，+∞）上单调递增

　　C．函数f（x）是偶函数且有最大值

　　D．函数f（x）是偶函数且有最小值

第Ⅱ卷（非选择题 共72分）

二、填空题：本大题共4个小题，每小题4分；共16分.将答案填在题中横线上.

13．某校学生会进行换届选举，现有高一学生代表2人，高二学生代表4人，高三学生代表2人，要从这些代表中选一人为学生会主席，共有的选法种数为　　　　　　  .

14．=　　　　　　　　　　 .

15．一个容量为n的样本分成若干组，已知某组的频数和频率分别为45和0.15，则n=　　　

16．已知曲线的一条切线的斜率为2，则切点的坐标为　　　　　　　 .

三、解答题：本大题共6个小题。解答应写出文字说明，证明过程或演算步骤.

17．（本小题满分8分）求下列函数的导数：

　 （1）；　 （2）

18．（本小题满分8分）按要求完成下列各题：

　 （1）计算　 （2）已知：.

19．（本小题满分8分）求展开式中含x³的项，并说明它是展开式中的第几项.

20．在冬季，某地居民对猪肉的需求情况的一组数据为（下图）：

价格x（万元）	12	11	10	9
需求量y（吨）	10	11	12	13

　 （1）求出y对x的回归方程；

　 （2）如果价格升为14万元/吨，请你预测猪肉的需求量是多少.

21．（本小题满分10分）用数学归纳法证明：能被9整除.

22．（本小题满分12分）当在（－1，+∞）是增函数，用反证法证明方程没有负根.

山东省济南市2007—2008学年第一学期教学质量检测试

高二数学（理科）参考答案

一、选择题：

1．C　2．B　3．A　4．C　5．B　6．D　7．D　8．B　9．A　10．A　11．C　12．C

2,4,6

二、填空题

13．8种　　  14．12　　　15．300　　　 16．

三、解答题：

17．解：（1）

（2）

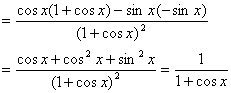
18．（1）解：

（2）证明：设

则左=

=

右=

=

左=右，即，得证

19．解：展开式的通项是

　　

依题意，有

所以，展开式中含x³的项为

它是展开式的第4项

20．解：（1）

序号	x	y	x2	y2	xy
1	12	10	144	100	120
2	11	11	121	121	121
3	10	12	100	144	120
4	9	13	81	169	117
	42	46	446	434	478

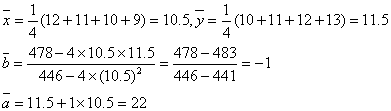
∴y对x的回归方程为

  （2）当x=14时，

21．证明：（1）当n=1时，（3+1）×7－1=27 能被9整除，命题成立

（2）假设当n=k时命题成立，即能被9整除

那么，当n=k+1时，

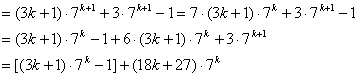
由归纳假设能被9整除及是9的倍数

所以能被9整除

即n=k+1时，命题成立

由（1）（2）知命题对任意的均成立

22．证明：假设

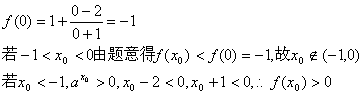
故

又与假设矛盾

∴方程没有负根。