高二年级数学上学期期末考试试卷(理科)
命题人,校对人:鞍山一中 张继红
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一个选项是符合题目要求的.
1. 向量![]() ,则
,则![]() 与
与![]() ( )
( )
A.相交 B.垂直 C.平行 D.以上都不对
2. 在![]() 中,
中, ![]() 则AC边长为
( )
则AC边长为
( )
A.![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
3. 过抛物线y=x2上的点M(![]() ,
, ![]() )的切线的倾斜角是
( )
)的切线的倾斜角是
( )
A ![]() B
B ![]() C
C ![]() D
D ![]()
4.设![]() 在
在![]() 上的图象是一条连续不间断的曲线,且在
上的图象是一条连续不间断的曲线,且在![]() 内可导,则下列结论中正确的是
( )
内可导,则下列结论中正确的是
( )
A. ![]() 在
在![]() 上的极值点一定是最值点 B.
上的极值点一定是最值点 B. ![]() 在
在![]() 上的最值点一定是极值点
上的最值点一定是极值点
C. ![]() 在
在![]() 上可能没有极值点
D.
上可能没有极值点
D. ![]() 在
在![]() 上可能没有最值点
上可能没有最值点
5.集合![]() ,
,![]() ,若
,若![]() 则实数P的取值范围是( )
则实数P的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
6.已知数列![]() ,如果
,如果![]() (
(![]() )是首项为1公比为
)是首项为1公比为![]() 的等比数列,那么
的等比数列,那么![]() 等于( )
等于( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
7.已知椭圆![]() 和双曲线
和双曲线![]() 有公共的焦点,那么双曲线的渐近线方程为( )
有公共的焦点,那么双曲线的渐近线方程为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
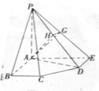
 8. 如图所示长方体ABCD—
8. 如图所示长方体ABCD—![]() 中,
中,![]() ,AD=1,
,AD=1,
点E、F、G分别是![]() 的中点,
的中点,
则异面直线![]() 和GF所成的角为
( )
和GF所成的角为
( )
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
9.已知函数![]() 的图象如图所示
的图象如图所示
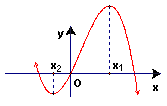 (
(![]() 为两个极值点),且
为两个极值点),且![]() 则有
( )
则有
( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
10.已知直线y=kx-k及抛物线![]() ,则
( )
,则
( )
A.直线与抛物线有且只有一个公共点
B.直线与抛物线有两个公共点
C.直线与抛物线有一个或两个公共点
D.直线与抛物线可能没有公共点
11已知梯形的两底的长度分别为![]() 。将梯形的两腰各分为n等份,连结两腰对应的分点,得到n-1条线段的长度之和为
( )
。将梯形的两腰各分为n等份,连结两腰对应的分点,得到n-1条线段的长度之和为
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
12.已知椭圆![]() ,过动点P的直线PA,PB分别与椭圆有且只有一个交点,交点为A、B,且
,过动点P的直线PA,PB分别与椭圆有且只有一个交点,交点为A、B,且![]() ,则动点P的轨迹是
( )
,则动点P的轨迹是
( )
A.圆 B.双曲线 C.椭圆 D.抛物线
二、填空题:本大题共4小题,每小题4分,共16分.
13.由曲线![]() 与
与![]() 所围成的图形的面积是 .
所围成的图形的面积是 .
14.已知x,y满足条件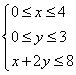 则z=2x+5y的最大值为
则z=2x+5y的最大值为
15.函数![]() 的最小值是
.
的最小值是
.
16. 给出下列三个命题
(1)设![]() 是定义在R上的可导函数,
是定义在R上的可导函数,![]() 为函数
为函数![]() 的导函数。
的导函数。![]() 是
是![]() 为
为![]() 极值点的必要不充分条件。
极值点的必要不充分条件。
(2)双曲线![]() 的焦距与m有关
的焦距与m有关
(3)命题“中国人不都是北京人”的否定是“中国人都是北京人”。
(4)命题“![]() ”
”
其中正确结论的序号是 。
三、解答题:本大题共6小题,共74分,解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分12分)
已知在△ABC中,角A、B、C所对的边分别为a,b,c,![]() ,求b,c及
,求b,c及![]()
18.(本小题满分12分)
数列{![]() }的前n项和记为
}的前n项和记为![]() ,
, ![]() 1=1,
1=1,![]()
![]() .
.
(1) 求{![]() }的通项公式;
}的通项公式;
(2) 等差数列{![]() }的各项为正数,其前n项和为
}的各项为正数,其前n项和为![]() ,且T3=15,又
,且T3=15,又![]() 1+
1+![]() 1,
1,![]() 2+
2+![]() 2,
2,![]() 3+
3+![]() 3成等比数列,求
3成等比数列,求![]()
19.(本小题满分12分)
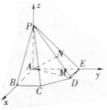
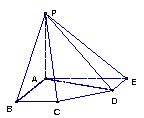 如图,在五棱锥P-ABCDE中,PA=AB=AE=2
如图,在五棱锥P-ABCDE中,PA=AB=AE=2![]() ,PB=PE=
,PB=PE=![]() ,BC=DE=
,BC=DE=![]() ,∠EAB=∠ABC=∠DEA=90O.
,∠EAB=∠ABC=∠DEA=90O.
(1) 求证:PA⊥平面ABCDE;
(2) 求二面角A-PD-E的大小.
20.(本小题满分12分)
定义在R上的函数ƒ(![]() )=
)=![]() 3+
3+![]()
![]() 2+
2+![]()
![]() (
(![]() ,
,![]() 为常数),在
为常数),在![]() =-1处取得极值,ƒ(
=-1处取得极值,ƒ(![]() )的图象在P(1,
ƒ(1))处的切线平行直线
)的图象在P(1,
ƒ(1))处的切线平行直线![]() =8
=8![]() ,
,
(1) 求函数ƒ(![]() )解析式及极值;
)解析式及极值;
(2) 求不等式ƒ(![]() )≥
)≥![]()
![]() 的解集;
的解集;
21.(本小题满分12分)
已知曲线C上任意一点M到点F(0,1)的距离比它到直线![]() =
=![]() 的距离小1.
的距离小1.
(1)求曲线C的方程;
(2)若过点P(2,2)的直线m与曲线C交于A,B两点,设![]() .
.
(i)当λ=1时,求直线m的方程;
(ii)当△AOB的面积为![]() 时(O为坐标原点),求λ的值.
时(O为坐标原点),求λ的值.
22.(本小题满分14分)
已知ƒ(![]() )=
)=![]() .
.
(1) 函数ƒ(![]() )在区间(0,+
)在区间(0,+![]() )上是增函数还是减函数?证明你的结论;
)上是增函数还是减函数?证明你的结论;
(2) 当![]() >0时,证明:ƒ(
>0时,证明:ƒ(![]() )>
)>![]() ;
;
(3) 求证:(1+1·2)(1+2·3)…[1+n(n+1)]>![]()
![]() .
.
2007—2008学年度上学期期末考试高二年级数学科试卷
理科答案
13、![]() 14、19 15、5 16、(1)(3)
14、19 15、5 16、(1)(3)
17、解:![]()
![]()
![]() ............3分
............3分
![]()
![]()
![]() ............6分
............6分
![]() b=
b=
当![]() b=3 c=5时
b=3 c=5时 ![]()
![]() ............10分
............10分
当b=5 c=3时 ![]()
![]() ............12分
............12分
18、解:(1)由![]() (n≥1)可得
(n≥1)可得![]() (n≥2),两式相减得
(n≥2),两式相减得![]() n+1-
n+1-![]() n=2
n=2![]() n,
n,![]() .
.
又![]() 2=2S1+1=3,
2=2S1+1=3,![]() ,故{
,故{![]() n}是首项为1,公比为3的等比数列,
n}是首项为1,公比为3的等比数列,![]() .
............6分
.
............6分
(2)设{![]() n}的公差为
n}的公差为![]() ,由T3=15可得
,由T3=15可得![]() 1+
1+![]() 2+
2+![]() 3=15,可得
3=15,可得![]() 2=5,故可设
2=5,故可设![]() 1=5-
1=5-![]() ,
,![]() 3=5+
3=5+![]() .
.
又![]() 1=1,
1=1,![]() 2=3,
2=3,![]() 3=9,由题意可得(5-
3=9,由题意可得(5-![]() +1)(5+
+1)(5+![]() +9)=(5+3)2,解得
+9)=(5+3)2,解得![]() 1=2,
1=2,![]() 2=-10.
2=-10.
![]() 等差数列{
等差数列{![]() n}的各项为正,
n}的各项为正,![]()
![]() =2,
=2,![]() .
.
............12分
19、解:(1)![]() PA=AB=2
PA=AB=2![]() ,PB=
,PB=![]() ,
,![]() PA2+AB2=PB2,
PA2+AB2=PB2,![]() ∠PAB=90O,即PA⊥AB.同理PA⊥AE.又
∠PAB=90O,即PA⊥AB.同理PA⊥AE.又![]() AB∩AE=A,
AB∩AE=A,![]() PA⊥平面ABCDE. ............4分
PA⊥平面ABCDE. ............4分
|
![]() AE⊥ED.
AE⊥ED. ![]() PA⊥平面ABCDE,
PA⊥平面ABCDE,![]() PA⊥ED.
PA⊥ED.
又![]() PA∩AE=A,
PA∩AE=A,![]() ED⊥平面PAE.过A作
ED⊥平面PAE.过A作
AG⊥PE于G,![]() DE⊥AG,
DE⊥AG,![]() AG⊥平面PDE.
AG⊥平面PDE.
过G作GH⊥PD于H,连结AH,由三垂线定理
得AH⊥PD. ![]() ∠AHG为二面角A-PD-E的平面
∠AHG为二面角A-PD-E的平面
角.在直角△PAE中,AG=![]() .在直角△PAD中,
.在直角△PAD中,![]() ,
,![]() 在直角△AHG中,sin∠AHG=
在直角△AHG中,sin∠AHG=![]() .
.
![]() ∠AHG=arcsin
∠AHG=arcsin![]() ,
,![]() 二面角A-PD-E的大小为arcsin
二面角A-PD-E的大小为arcsin![]() . ............12分
. ............12分
|
C(2![]() ,
,![]() ,0),过A作AN⊥PD于N.
,0),过A作AN⊥PD于N.
![]() (
(![]() ,2
,2![]() ,-2
,-2![]() ),
),
设![]() ,
,
![]() =(
=(![]()
![]() ,2
,2![]()
![]() ,2
,2![]() -2
-2![]()
![]() ).
). ![]() AN⊥PD,
AN⊥PD, ![]() .
.![]()
![]() ·
·![]()
![]() +2
+2![]() ·2
·2![]()
![]() -2
-2![]() (2
(2![]() -2
-2![]()
![]() )=0.解得
)=0.解得![]() .
. ![]() ,即
,即![]() ,同理,过E作EM⊥PD于M,则
,同理,过E作EM⊥PD于M,则![]() .二面角A-PD-E的大小为
.二面角A-PD-E的大小为![]() ,
,![]() 所成的角<
所成的角<![]() >.
>. ![]() cos<
cos<![]() >=
>=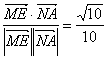 .
.![]() <
<![]() >=arccos
>=arccos ![]() .
.![]() 二面角A-PD-E的大小为arccos
二面角A-PD-E的大小为arccos![]() . ............12分
. ............12分
20、解: (1)由题设知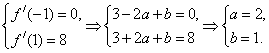
![]() ƒ(
ƒ(![]() )=
)=![]() 3+2
3+2![]() 2+
2+![]() ,
,
则![]() ,
,
令![]() ,
,
当![]() 变化时,ƒ(
变化时,ƒ(![]() )
)![]() 的变化情况如下表:
的变化情况如下表:
|
| (- | -1 | (-1, |
| ( |
|
| + | 0 | - | 0 | + |
| ƒ( | ↑ | 0 | ↓ |
| ↑ |
![]() ƒ(
ƒ(![]() )的极大值为ƒ(-1)=0,极小值为ƒ(
)的极大值为ƒ(-1)=0,极小值为ƒ(![]() )=
)=![]() .............6分
.............6分
(2)![]() 3+2
3+2![]() 2+
2+![]() ≥
≥![]()
![]()
![]() .
.
考虑方程![]() 根的情况,
根的情况,
若![]() >0,则方程
>0,则方程![]() 的根为
的根为![]() ,
,
①当![]() >1时,
>1时,![]() ,
,
![]() ;
;
②![]() =1时,不等式的解集为
=1时,不等式的解集为![]() ;
;
③0<![]() <1时,
<1时,![]() ;
;
若![]() =0时,不等式的解集为
=0时,不等式的解集为![]() ;
;
若![]() <0时,不等式的解集为
<0时,不等式的解集为![]() .............12分
.............12分
21、解: (1)解法一
设![]()
当![]() ≥-2时;
≥-2时;![]() ;
;
当![]() <-2时,
<-2时,![]()
两边平方得![]() ,因
,因![]() <-2,不合题意,舍去.
<-2,不合题意,舍去.
故点M的轨迹C的方程是:![]() .
............4分
.
............4分
解法二 ∵点M到点F(0,1)的距离比它到直线![]() =-2的距离小1.
=-2的距离小1.
∴点M在直线![]() 的上方. ∴点M到F(0,1)的距离与它到直线
的上方. ∴点M到F(0,1)的距离与它到直线![]() =-1的距离相等.
=-1的距离相等.
∴点M的轨迹C是以F为焦点![]() 为准线的抛物线,所以曲线C的方程为
为准线的抛物线,所以曲线C的方程为![]() .
.
(2)当直线m的斜率不存在时,它与曲线C只有一个交点,不合题意,
当直线m与![]() 轴不垂直时,设直线m的方程为
轴不垂直时,设直线m的方程为![]() .
.
代入![]() 得,
得,
![]() ①
①
![]() >0对k∈R恒成立.
>0对k∈R恒成立.
∴直线m与曲线C恒有两个不同的交点。
设交点A,B的坐标分别为A(![]() )B(
)B(![]() ),则
),则![]() .
. ![]() .
.
(i)由![]() ,且λ=1得,P为AB的中点,
,且λ=1得,P为AB的中点,
∴![]() .把②代入得,
.把②代入得,![]() .∴直线m的方程是
.∴直线m的方程是![]() .
.
............6分
(ii)![]() =
=
![]() .
.
点O到直线m的距离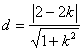 .
.
![]() =
=![]() ·
·![]() =
=![]()
∵![]() =
=![]()
∴![]() .
.
(![]() (无实根)
(无实根)
由![]()
1°当k=0时,方程①的解为![]() .
.
当![]() =
=![]() ;
;
当![]() . ...........10分
. ...........10分
2°当k=2时,方程①的解为![]() ,
,
同理可得,![]() .
............12分
.
............12分
22、解:(1)![]()
![]()
![]()
因此函数ƒ(![]() )在区间(0,+
)在区间(0,+![]() )上是减函数. ............3分
)上是减函数. ............3分
(2)证明:当![]() >0时,ƒ(
>0时,ƒ(![]() )>
)>![]() 成立,即证当
成立,即证当![]() >0时,(
>0时,(![]() +1)ln(
+1)ln(![]() +1)+1-2
+1)+1-2![]() >0成立.
>0成立.
令g(![]() )=(
)=(![]() +1)ln(
+1)ln(![]() +1)+1-2
+1)+1-2![]() ,则
,则![]() ,
,
![]()
![]() .
.
![]() .
............8分
.
............8分
(3)由(2)知:![]() ,
,
![]() ,
,
令![]() .
.
![]() ln(1+1·2)+ln(1+2·3)+…+ln[1+n(n+1)]
ln(1+1·2)+ln(1+2·3)+…+ln[1+n(n+1)]
>![]()
=![]()
![]()
=![]() ,
,
![]() .
............14分
.
............14分