高二年级第二学期月考试题
数学学科(理科)月考试题
一．选择题（在每题给出的四个选项中，只有一项是最符合题目要求的。共12，60分）
1. 
等于(
D )
A. 
B. 
C. 
D.
2. 
=( B )
A. 
B. 
C. 
D.
3．把9个相同的小球放入其编号为1，2，3的三个盒子里，要求每个盒子放球的个数不小于其编号数，则不同的放球方法共有( B )
A．8种 B．10种 C．12种 D．16种
4．若
的展开式中
的系数是80，则实数a的值为( D )
A．-2 B．
C．
D．2
5．平面
、
、
两两互相垂直，点
，点A到、的距离都是3，P是上的动点，P到的距离是到点A距离的2倍，则点P的轨迹上的点到的距离的最小值是( A
)
A．
B．
C．
D．
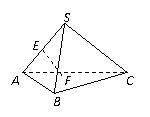
6．如图，在正四面体S—ABC中，E为SA的中点，F为DABC的
中心，则异面直线EF与AB所成的角是( C )
A．30° B．45°
C．60° D．90°
7．某次文艺汇演，要将A、B、C、D、E、F这六个不同节目编排成节目单，如下表：
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 |
| 节目 |
如果A、B两个节目要相邻，且都不排在第3号位置，那么节目单上不同的排序方式有（ B ）
A．192种 B．144种 C．96种 D．72种
8．已知
，若
= 29－n，那么自然数n的值为（ B
）
A．3
B．
9．顶点往同一球面上的正四棱柱ABCD－
中，AB=1，AA′=
，则A、C两点间的球面距离为( C )
A、
B、
C、
D、
10.若
展开式中各项系数之和为
,则展开式中含
的项是(B)
（A）第3项 （B）第4项 （C）第5项 （D）第6项
11、设
、
表示两条直线,
、
表示两个平面,下列命题中真命题是( D )
（A）若
则
（B）若
则
（C）若
,则
（D）若
,则
12. 12.半径为4的球面上有A、B、C、D四点，且AB，AC，AD两两互相垂直，则
、
、
面积之和
的最大值为 （ C ）
A．8 B．
二、填空题: 本大题共4小题，每小题5分，共20分，把答案填在题中横线上。
13.若正四棱锥的底面对角线的长为
,体积为
,则侧面与底面所成的二面角等于____________
14.如图：在正三棱柱
中,已知AB=1,D在
上,且BD=1,若AD与侧面
所成的角为,则
的值为 ． 
15．某校要求每位学生从
门课程中选修
门，其中甲、乙两门课程至少选修一门，则不同的选课方案有 种（以数字作答）．50
16.已知
的展开式中的常数项为
，则非零实数
的值是 ．1
三、简答题：本大题共4小题，共40分，解答应写出文字说明，证明过程或演算步骤。
17.100件产品中有97件合格品,3件次品,从中任取5件产品进行检查,
(1)抽出的5件产品都是合格品的抽法有多少种?
(2)抽出的5件产品恰好有2件是次品的抽法有多少种?
(3)抽出的5件产品至少有2件是次品的抽法有多少种?
442320
446976
18. 在
的展开式中,某一项的系数恰好是它前一项系数的2倍,而等于它后一项系数的
,试求展开式中二项式系数最大的项.
n=7 
,
19. 
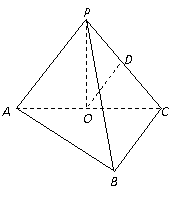在三棱锥P—ABC中，
，点O、D分别是AC、PC的中点，
底面ABC.（1）求证OD∥平面PAB；
（2）求二面角A—BC—P的大小.
20. 如图，四棱锥P—ABCD中， PA
平面ABCD，底面ABCD是直角梯形，AB⊥AD，CD⊥AD，CD=2AB，E为PC中点．
(I) 求证：平面PDC平面PAD；
(II) 求证：BE//平面PAD．
19．（1）∵O、D分别为AC、PC的中点，∴OD∥PA. 又PA
平面PAB，∴OD∥平面PAB.
（2）∵
又∵平面ABC，∴PA=PB=PC，
取BC中点E，连结PE和OE，则
∴
是所求二面角的平面角.
又
，易求得
在直角
中，
，
∴二面角A—BC—P的大小为
20．证明：（1）由PA平面ABCD
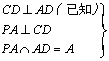
平面PDC平面PAD；
（2）取PD中点为F，连结EF、AF，由E为PC中点，
得EF为△PDC的中位线，则EF//CD，CD=2EF．
又CD=2AB，则EF=AB．由AB//CD，则EF∥AB．
所以四边形ABEF为平行四边形，则EF//AF．
由AF
面PAD，则EF//面PAD．