高二数学计数原理练习

高二数学计数原理练习（一）

第一章 

A组题（共100分）

一．选择题：本大题共5题，每小题7分，共35分。在每小题给出的四个选项中，只有一项是符合题目要求的.

1、某商店销售的电视机中，本地产品有4种，外地产品有6种，现购买一台电视机，不同的选法有（　　）

A.10种　　　B.24种　　  C. 种　　　D. 种

2、从A地到B地有2条路，从B地到C地有5条路，某人从A地经B地到C地，则此人所经线路有（　  ）

A.7种　　　B.10种　　  C. 种　　　D. 种

3、从4种蔬菜品种中选出3种，分别种植在3块不同的土地上，不同种植方法的种类数是（　　）

A.36　　　 B.64　　　　 C.24　　　　 D.81

4、的展开式第5项的系数是（　　 ）

A.　　　  B. 　　　　 C. 　　　　 D.

5、若，则（　　）

A.1　　　　  B.－1　　　　　 C. 　　　　　D.

二．填空题：本大题共4小题，每小题6分，共24分.

6、计算_________.

7、从4名男生和3名女生中选3人参加一项活动，若女生甲必须参加，则不同的选法种数是___________.

8、________.

9、中常数项是__________________.

三．解答题：本大题共3小题，共41分，解答题应写出文字说明、证明过程或演算步骤.

10、（本题13分）计算下列各题： ⑴　　　　 ⑵

11、（本题14分）有四个男生和三个女生排成一排，按下列要求，各有多少种不同排法？

⑴男生甲排在正中间；⑵男生甲不排在两端；⑶三个女生排在一起；⑷三个女生两两都不相邻.

12、（本题14分）已知，求的展开式中的系数.

B组题（共100分）

四．选择题：本大题共5题，每小题7分，共35分。在每小题给出的四个选项中，只有一项是符合题目要求的.

13．已知集合，则集合到集合的映射的个数是（　 ）

A．81　　　　  B．64　　　　 C．24　　　　D．4

14．从4双不同的鞋中任取4只，恰有两只配成一双的取法有（　 ）

A．24种　　　 B．16种　　　 C．32种　　　D．48种

15．从6人中选4人，分别到四个城市游览，要求每个城市有1人游览，每人只能游览一个城市，又知道这6人中，甲、乙两人都不去城市游览，则不同的选择方案有（　 ）

A．300种　 B．240种　　C．144种　　D．96种

16．若，则的个位数字是（　 ）

A．　　B．　　C．　 D．

17．的展开式中，含的正整数次幂的项共有（　 ）

A．4项　　B．3项　　 C．2项　　 D．1项

五．填空题：本大题共4小题，每小题6分，共24分.

18．有编号为1、2、3、4的四个盒子，现将10个完全相同的小球放入这四个盒子中，每个盒子至少放一个小球，则不同的放法有　　　　　　　　　 种.

19．过三棱柱任意两个顶点的直线共有15条，其中构成异面直线的有　　　　  对.

20．“渐升数”是指每个数字比其左边的数字大的正整数（如12578），若把所有的五位渐升数按从小到大的顺序排列，则第100个数是　　　　　　　　 .

21．在的展开式中，常数项为　　　　　　  .

六．解答题：本大题共3小题，共41分，解答题应写出文字说明、证明过程或演算步骤.

22．（本题13分）

解不等式．

 

23．（本题14分）

由四个不同数字1，2，4，组成无重复数字的三位数，

⑴若，其中能被5整除的共有多少个？

⑵若，其中的偶数共有多少个？

⑶若所有这些三位数的各位数字之和是252，求.

24．（本题14分）

⑴设，求证：　.

⑵求证：对任何自然数，都可以被676整除.

C组题（共50分）

七、选择或填空：本大题共2题，每小题7分，共14分．

25、n+1个不同的球放入n个不同的盒子中，其放法总数为的放法是（　　）

A、指定某盒放3球，此外最多放1球　 B、恰有一盒放3球，此外最多放1球

C、恰有一盒放2球，此外最多放1球　 D、恰有3盒放2球，此外最多放1球

26、对于正整数n和m，其中m＜n，定义其中k是满足n＞km的最大整数，则___________．

八、解答题：本大题共2小题，共36分，解答题应写出文字说明、证明过程或演算步骤．

27、（本题18分）

设数列是等比数列，，公比q是的展开式中的第二项（按x的降幂排列）．

（1）用n、x表示通项a_n与前n项和S_n；

（2）若，用x、n表示A_n．

28、（本题18分）

已知i、m、n是正整数，且1＜i≤m＜n　．

（1）证明：；

（2）证明：（1+m）ⁿ＞（1+n）^m　．

厦门市2007—2008学年选修2-3练习（一）答案

A组答案

1～5. ABCCB　6.1540 7.20　8.256　9.－160

10、解：⑴原式=

⑵由

∴原式

11、解：⑴，∴男生甲排在正中间的排法有720种；

⑵，∴男生甲不排在两端的排法有3600种；

⑶，∴三个女生排在一起的排法有720种；

⑷，∴三个女生两两都不相邻的排法有144种.

12、解：∵，∴

∴在中，

令得

∴，

∴的系数是126.

B组答案：

13～17：BDBAC　 18．84　 19．36　　 20．24789　　21．15

22．解：原不等式化为：

解得

又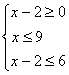得且

∴原不等式的解集为.

23．解：⑴由要求知：5只能在个位，故能被5整除的三位数有个

⑵当0在个位时，三位数有个

当2或4在个位是，三位数有个

∴当时，三位偶数共有个

⑶易知：

∵1，2，4，在各个数位上出现的次数都相同，且各自出现次

∴数字之和为

∴，解得.

24．证明：⑴设，则，

∴原不等式等价于：

∵

∴原不等式成立.

⑵

∵

∴都可被676整除.

C组答案

25、　B　　　 26、

27、解：（1）∵

∴ 即

∴ m=3

由知：

∴　，

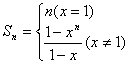
　　　　（2）当x=1时，　．

　 　．

 ∴　　．

两式相加得：　　．

∴　．

当x≠1时，　　．

∴

　　 =

　　 =

　　 =

综上，得　　．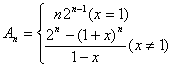

28、证明：（1）　　，

　　　　　　  　　，

　　　　 对于m＜n，当k=1，2，…，i-1，有

　　　　 ∴ ，　　∴　　．

　　　　 （2）由二项式定理：

　　　　　　　　　　　　　  又∵，，而

　　　　　　　　  ∴　 ∴，，

　　　　　　　　　　　　 ……，

　　　　　　　 又∵，

 ∴．