高二数学直线与圆锥曲线同步测试1

安陆一中高二数学同步测试直线与圆锥曲线(一)

一、选择题

1.斜率为1的直线l与椭圆+y²=1相交于A、B两点，则AB的最大值为(　　)

A.2　　　　　　　　　　　 B. 　　　　　　　　　　　C.　　　　　　　　　　　　　　 D.

2.抛物线y=ax²与直线y=kx+b(k≠0)交于A、B两点，且此两点的横坐标分别为x₁,x₂,直线与x轴交点的横坐标是x₃,则恒有(　　)

A.x₃=x₁+x₂ B.x₁x₂=x₁x₃+x₂x₃

C.x₁+x₂+x₃=0　　　　　　　　　　　　　　　　　　　　　　D.x₁x₂+x₂x₃+x₃x₁=0

3. (浙江)函数y＝ax²＋1的图象与直线y＝x相切，则a＝(　　 )

(A) 　　(B)　　 (C) 　　 (D)1

4. （上海）过抛物线的焦点作一条直线与抛物线相交于A、B两点，它们的横坐标之和等于5，则这样的直线（ 　）

A．有且仅有一条　　 B．有且仅有两条　　　C．有无穷多条　　　D．不存在

5. （山东卷）设直线关于原点对称的直线为，若与椭圆的交点为A、B、，点为椭圆上的动点，则使的面积为的点的个数为（　　 ）

（A）1　　　　　　　　　 （B）2　　　　　  （C）3　　　　（D）4

6. (全国卷Ⅰ)已知双曲线的一条准线为，则该双曲线的离心率为（　　 ）

（A）　　　　　　　　　 （B）　　　　　　　 （C）　　　　　　（D）

7. (全国卷III)设椭圆的两个焦点分别为F1、、F2，过F2作椭圆长轴的垂线交椭圆于点P，若△F1PF2为等腰直角三角形，则椭圆的离心率是（　　）

（A）　　　　　  （B）　　　　（C）　 （D）

8.（湖南卷）已知双曲线－＝1（a＞0，b＞0）的右焦点为F，右准线与一条渐近线交于点A，△OAF的面积为（O为原点），则两条渐近线的夹角为(　　）

　　A．30º　　　　B．45º　　　　C．60º　　　　D．90º

9. （福建卷）已知定点A、B且AB=4，动点P满足PA－PB=3，则PA的最小值是　　　（  ）

　　　 A．　 　　　B．　 　　　C．　　　D．5

10. （广东卷）若焦点在轴上的椭圆的离心率为，则m=(　　　)

（Ａ）　　（Ｂ）　　（Ｃ）　 （Ｄ）

二、填空题

11.已知两点M(1，)、N(－4，－)，给出下列曲线方程：①4x+2y－1=0,

②x²+y²=3,③+y²=1,④－y²=1,在曲线上存在点P满足MP=NP的所有曲线方程是_________.

12.正方形ABCD的边AB在直线y=x+4上，C、D两点在抛物线y²=x上，则正方形ABCD的面积为_________.

13.在抛物线y²=16x内，通过点(2，1)且在此点被平分的弦所在直线的方程是_________.

三、解答题

14.已知抛物线y²=2px(p＞0),过动点M(a,0)且斜率为1的直线l与该抛物线交于不同的两点A、B，且AB≤2p.

(1)求a的取值范围.

(2)若线段AB的垂直平分线交x轴于点N，求△NAB面积的最大值.

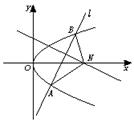
15.已知中心在原点，顶点A₁、A₂在x轴上，离心率e=的双曲线过点P(6，6).

(1)求双曲线方程.

(2)动直线l经过△A₁PA₂的重心G，与双曲线交于不同的两点M、N，问：是否存在直线l,使G平分线段MN，证明你的结论.

16.已知双曲线C的两条渐近线都过原点，且都以点A(，0)为圆心，1为半径的圆相切，双曲线的一个顶点A₁与A点关于直线y=x对称.

(1)求双曲线C的方程.

(2)设直线l过点A，斜率为k,当0＜k＜1时，双曲线C的上支上有且仅有一点B到直线l的距离为，试求k的值及此时B点的坐标.

17.已知椭圆的中心在坐标原点O，焦点在坐标轴上，直线y=x+1与椭圆交于P和Q，且OP⊥OQ，PQ=，求椭圆方程.

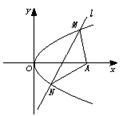
18.如图所示，抛物线y²=4x的顶点为O，点A的坐标为(5，0)，倾斜角为的直线l与线段OA相交(不经过点O或点A)且交抛物线于M、N两点，求△AMN面积最大时直线l的方程，并求△AMN的最大面积.

19. 已知双曲线C：2x²－y²=2与点P(1，2)

(1)求过P(1，2)点的直线l的斜率取值范围，使l与C分别有一个交点，两个交点，没有交点.

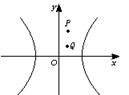(2)若Q(1，1)，试判断以Q为中点的弦是否存在.

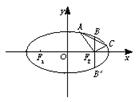
20.如图，已知某椭圆的焦点是F₁(－4，0)、F₂(4，0)，过点F₂并垂直于x轴的直线与椭圆的一个交点为B，且F₁B+F₂B=10，椭圆上不同的两点A(x₁,y₁),C(x₂,y₂)满足条件：F₂A、F₂B、F₂C成等差数列.

(1)求该弦椭圆的方程；

(2)求弦AC中点的横坐标；

(3)设弦AC的垂直平分线的方程为y=kx+m，求m的取值范围.

直线与圆锥曲线(一) 参考答案

一、选择题

1.. C　　 2. B　　 3.B 　 4.B 　 5.B 　　6.A　　 7.D 　 8.D　　9. C 　 10.B

二、填空题

11.解析：点P在线段MN的垂直平分线上，判断MN的垂直平分线于所给曲线是否存在交点.

答案：②③④

12.解析：设C、D所在直线方程为y=x+b,代入y²=x,利用弦长公式可求出CD的长，利用CD的长等于两平行直线y=x+4与y=x+b间的距离，求出b的值，再代入求出CD的长.

答案：18或50

13.解析：设所求直线与y²=16x相交于点A、B，且A(x₁,y₁),B(x₂,y₂),代入抛物线方程得y₁²=16x₁,y₂²=16x₂,两式相减得，(y₁+y₂）(y₁－y₂)=16(x₁－x₂).

即k_AB=8.

故所求直线方程为y=8x－15.

答案：8x－y－15=0

三、解答题

14.解：(1)设直线l的方程为：y=x－a,代入抛物线方程得(x－a)²=2px,即x²－2(a+p)x+a²=0

∴AB=≤2p.∴4ap+2p²≤p²,即4ap≤－p²

又∵p＞0,∴a≤－.

(2)设A(x₁,y₁)、B(x₂,y₂)，AB的中点 C(x,y),

由(1)知，y₁=x₁－a,y₂=x₂－a,x₁+x₂=2a+2p,

则有x==p.

∴线段AB的垂直平分线的方程为y－p=－(x－a－p),从而N点坐标为(a+2p,0）

点N到AB的距离为

从而S_△NAB=

当a有最大值－时，S有最大值为p².

15.解：(1)如图，设双曲线方程为=1.由已知得,解得a²=9,b²=12.

所以所求双曲线方程为=1.

(2)P、A₁、A₂的坐标依次为(6,6)、(3，0)、(－3，0），

∴其重心G的坐标为(2，2）

假设存在直线l，使G(2，2)平分线段MN，设M(x₁,y₁)，N(x₂,y₂).则有

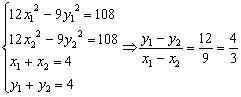，∴k_l=

∴l的方程为y= (x－2)+2,

由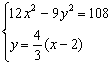,消去y,整理得x²－4x+28=0.

∵Δ=16－4×28＜0,∴所求直线l不存在.

16.解：(1)设双曲线的渐近线为y=kx,由d==1,解得k=±1.

即渐近线为y=±x,又点A关于y=x对称点的坐标为(0，).

∴a==b,所求双曲线C的方程为x²－y²=2.

(2)设直线l：y=k(x－)(0＜k＜1,依题意B点在平行的直线l′上，且l与l′间的距离为.

设直线l′：y=kx+m,应有,化简得m²+2km=2.　　　　　　　　　　　　　 ②

把l′代入双曲线方程得(k²－1)x²+2mkx+m²－2=0,

由Δ=4m²k²－4(k²－1)(m²－2)=0.可得m²+2k²=2　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ③

②、③两式相减得k=m,代入③得m²=,解设m=,k=,此时x=,y=.故B(2,).

17.解：设椭圆方程为mx²+ny²=1(m＞0,n＞0)，

P(x₁,y₁),Q(x₂,y₂)

由 得(m+n)x²+2nx+n－1=0,

Δ=4n²－4(m+n)(n－1)＞0,即m+n－mn＞0,

由OP⊥OQ,所以x₁x₂+y₁y₂=0,即2x₁x₂+(x₁+x₂)+1=0,

∴+1=0,∴m+n=2　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ①

又2²,

将m+n=2,代入得m·n=　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　②

由①、②式得m=,n=或m=,n=

故椭圆方程为+y²=1或x²+y²=1.

18.解：由题意，可设l的方程为y=x+m,－5＜m＜0.

由方程组,消去y,得x²+(2m－4)x+m²=0　　　　　　　　　　 　　　　　　　  ①

∵直线l与抛物线有两个不同交点M、N，

∴方程①的判别式Δ=(2m－4)²－4m²=16(1－m)＞0,

解得m＜1,又－5＜m＜0,∴m的范围为(－5，0)

设M(x₁,y₁),N(x₂,y₂)则x₁+x₂=4－2m，x₁·x₂=m²,

∴MN=4.

点A到直线l的距离为d=.

∴S_△=2(5+m),从而S_△²=4(1－m)(5+m)²

=2(2－2m)·(5+m)(5+m)≤2()³=128.

∴S_△≤8,当且仅当2－2m=5+m,即m=－1时取等号.

故直线l的方程为y=x－1，△AMN的最大面积为8.

19.解：(1)当直线l的斜率不存在时，l的方程为x=1,与曲线C有一个交点.当l的斜率存在时，设直线l的方程为y－2=k(x－1),代入C的方程，并整理得

(2－k²)x²+2(k²－2k)x－k²+4k－6=0　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (^*)

(ⅰ)当2－k²=0,即k=±时，方程(^*)有一个根，l与C有一个交点

(ⅱ)当2－k²≠0,即k≠±时

Δ=［2(k²－2k)］²－4(2－k²)(－k²+4k－6)=16(3－2k)

①当Δ=0,即3－2k=0,k=时，方程(^*)有一个实根，l与C有一个交点.

②当Δ＞0,即k＜,又k≠±,故当k＜－或－＜k＜或＜k＜时，方程(^*)有两不等实根，l与C有两个交点.

③当Δ＜0，即k＞时，方程(^*)无解，l与C无交点.

综上知：当k=±,或k=，或k不存在时，l与C只有一个交点；

当＜k＜,或－＜k＜,或k＜－时，l与C有两个交点；

当k＞时，l与C没有交点.

(2)假设以Q为中点的弦存在，设为AB，且A(x₁,y₁),B(x₂,y₂)，则2x₁²－y₁²=2,2x₂²－y₂²=2两式相减得：2(x₁－x₂)(x₁+x₂)=(y₁－y₂)(y₁+y₂)

又∵x₁+x₂=2,y₁+y₂=2

∴2(x₁－x₂)=y₁－y₁

即k_AB==2

但渐近线斜率为±,结合图形知直线AB与C无交点，所以假设不正确，即以Q为中点的弦不存在.

20.解：(1)由椭圆定义及条件知，2a=F₁B+F₂B=10,得a=5,又c=4,所以b==3.

故椭圆方程为=1.

(2)由点B(4,y_B)在椭圆上，得F₂B=y_B=.因为椭圆右准线方程为x=,离心率为，根据椭圆定义，有F₂A=(－x₁),F₂C=(－x₂)，

由F₂A、F₂B、F₂C成等差数列，得

(－x₁)+(－x₂)=2×,由此得出：x₁+x₂=8.

设弦AC的中点为P(x₀,y₀),则x₀==4.

(3)解法一：由A(x₁,y₁),C(x₂,y₂)在椭圆上.

① ②

得　　　　　　　　　　　　　　　　

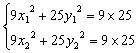
①－②得9(x₁²－x₂²)+25(y₁²－y₂²)=0,

即9×=0(x₁≠x₂)

将 (k≠0)代入上式，得9×4+25y₀(－)=0

(k≠0)

即k=y₀(当k=0时也成立).

由点P(4，y₀)在弦AC的垂直平分线上，得y₀=4k+m,所以m=y₀－4k=y₀－y₀=－y₀.

由点P(4，y₀)在线段BB′(B′与B关于x轴对称)的内部，得－＜y₀＜,所以－＜m＜.

解法二：因为弦AC的中点为P(4,y₀)，所以直线AC的方程为

y－y₀=－(x－4)(k≠0)　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　③

将③代入椭圆方程=1,得

(9k²+25)x²－50(ky₀+4)x+25(ky₀+4)²－25×9k²=0

所以x₁+x₂==8,解得k=y₀.(当k=0时也成立)

(以下同解法一).