高二级数学线性规划测试及答案

（6）线性规划

一、选择题（本大题共10小题，每小题5分，共50分）

1．设直线l的方程为：，则下列说法不正确的是　　　　　　　　　　　　　　　 （　　）

　　　 A．点集{}的图形与x轴、y轴围成的三角形的面积是定值　　　

B．点集{}的图形是l右上方的平面区域

　　　 C．点集{}的图形是l左下方的平面区域

　　 D．点集{}的图形与x轴、y轴围成的三角形的面积有最小值

2．已知x, y满足约束条件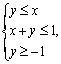的最大值为 　　　　　　　　　　　　　　　 （　　）

　　　 A．3　　　　　　　　　　　　B．－3　　　　　　　　　　 C．1　　　　　　　　　　　　D．

3．如果函数的图象与x轴有两上交点，则点（a，b）在aOb平面上的区

　 域（不包含边界）为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　　　　　　　　 A．　　　　　　  B．　　 　　　 C．　　　　　　　 D．

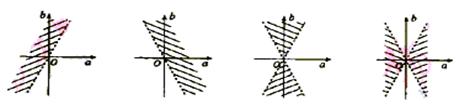
4．图中的平面区域（阴影部分包括边界）可用不等式组表示为　　　　　　　　　　　　　　　（　　）

　　　 A．　　　　　　　　　　　　　　　　　　　　　B．

　　　 C．　　　　　　　　　　　　　　　　　　　　D．

5．不等式组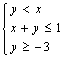，表示的区域为D，点P₁（0，-2），P₂（0，0），则　　　　　　　　（　　）

A．　　　　　　　　　　　　　　　　B．　　　　　　　　　　　　

C．　　　　　　　　　　　　　　　　 D．

6．已知点P（x₀，y₀）和点A（1，2）在直线的异侧，则　　　　　　（　　）

A．　　　　　　　　　　　　　　　　　 B．0　　

C．　　　　　　　　　　　　　　　　　　D．

7．已知点P（0，0），Q（1，0），R（2，0），S（3，0），则在不等式表示的平面区域内的点是　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．P、Q　　　　　　　　　B．Q、R　　　　　　　　　C．R、S　　　　　　　　　D．S、P

8．在约束条件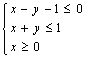下，则目标函数的最优解是　　　　　　　　　　 （　　）

　 A．（0，1），（1，0） 　　　　　　　　　　　　　B．（0，1），（0，-1）

C．（0，-1），（0，0）　　　　　　　　　　　　　D．（0，-1），（1，0）

9．满足的整点的点（x，y）的个数是　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．5　　　　　　　　　　　　B．8　　　　　　　　　　　　C．12　　　　　　　　　　　D．13

10．某厂生产甲、乙两种产品，产量分别为45个、50个，所用原料为A、B两种规格的金属板，每张面积分别为2m²、3 m²，用A种金属板可造甲产品3个，乙产品5个，用B种金属板可造甲、乙产品各6个，则A、B两种金属板各取多少张时，能完成计划并能使总用料面积最省？　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

A．A用3张，B用6张　　　　　　　　　　　　　　B．A用4张，B用5张

C．A用2张，B用6张　　　　　　　　　　　　　　D．A用3张，B用5张

二、填空题（本题共4小题，每小题6分，共24分）

11．表示以A（0，0），B（2，2），C（2，0）为顶点的三角形区域（含边界）的不等式组是

　　　　　 　　　　　　　　

12．已知点P（1，-2）及其关于原点的对称点均在不等式表示的平面区域内，则b的取值范围是　　　　　　　　　　　　　．

13．已知点（x，y）在不等式组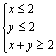表示的平面区域内，则的取值范围为

　　　　　　　　　　　　　　　　　　．

14．不等式所表示的平面区域的面积是　　　　　　　　　　　　　　　

三、解答题（本大题共6题，共76分）

15．画出不等式组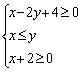所表示的平面区域．（12分）

16． 求由约束条件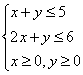确定的平面区域的面积和周长．（12分）

17．求目标函数的最大值及对应的最优解，约束条件是．

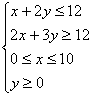（12分）

18．设，式中变量满足条件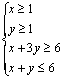，求z的最小值和最大值．（12分）

19．A市、B市和C市分别有某种机器10台、10台和8台．现在决定把这些机器支援给D市18台，E市10台．已知从A市调运一台机到D市、E市的运费分别为200元和800元；从B市调运一台机器到D市、E市的运费分别为300元和700元；从C市调运一台机器到D市、E市的运费分别为400元和500元．设从A市调x台到D市，B市调y台到D市，当28台机器全部调运完毕后，用x、y表示总运费W（元），并求W的最小值和最大值．（14分）

20．某纺纱厂生产甲、乙两种棉纱，已知生产甲种棉纱1吨需耗一级子棉2吨、二级子棉1　 吨；生产乙种棉纱需耗一级子棉1吨、二级子棉2吨，每1吨甲种棉纱的利润是600元，每1吨乙种棉纱的利润是900元，工厂在生产这两种棉纱的计划中要求消耗一级子棉不超过300吨、二级子棉不超过250吨．甲、乙两种棉纱应各生产多少(精确到吨)，能使利润总额最大?（14分）

参考答案

一．选择题（本大题共10小题，每小题5分，共50分）

题号	1	2	3	4	5	6	7	8	9	10
答案	C	A	C	C	C	D	C	D	D	A

二．填空题（本大题共4小题，每小题6分，共24分）

11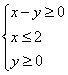． 　　12． 　　 13．[2，4]　　 14． 2

三、解答题（本大题共6题，共76分）

15．（12分）

16．（12分）

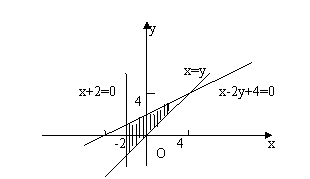
[解析]：由约束条件作出其所确定的平面区域（阴影部分），其四个顶点为O（0，0），B（3，0），A（0，5），P（1，4）．过P点作y轴的垂线，垂足为C．

　　则AC=5-4=1，PC=1-0=1，OC=4，OB=3，AP=，

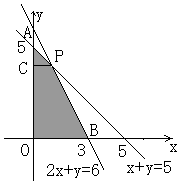PB=

得=，

　　 所以=+=，

　　　　 =OA+AP+PB+OB=8++

17．（12分）

 [解析]：作出其可行域如图所示，

约束条件所确定的平面区域的五个顶点为（0，4），（0，6），（6，0）（10，0），（10，1），

　　 作直线l₀：10 x +15 y =0，再作与直线l₀平行的直线l：10 x +15 y =z，

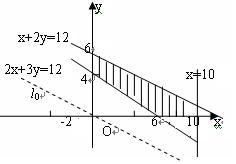　　 由图象可知，当l经过点（10，1）时使取得最大值，

　　 显然，

此时最优解为（10，1）．

18．（12分）

[解析]：作出其可行域如图所示，

约束条件所确定的平面区域的四个顶点为（1，），（1，5），（3，1），（5，1），

　　 作直线l₀：2 x + y =0，再作与直线l₀平行的直线l：2 x + y =z，

　　 由图象可知，当l经过点（1，）时

使取得最小值，

　　　

　　 当l经过点（5，1）时使取得最大值，

　　　

19．（14分）

[解析]：由题意可得，A市、B市、C市调往D市的机器台数分别为x、y、（18- x - y），调往E市的机器台数分别为（10- x）、（10- y）、[8-（18- x - y）]．于是得

W=200 x +800(10- x)+300 y +700(10- y)+400(18- x - y)+500[8-（18- x - y）]

　　　　　　 =-500 x -300 y +17200

　　　　　设Ｗ＝17200－100T，其中Ｔ＝5 x +3 y ,

　　　又由题意可知其约束条件是

　

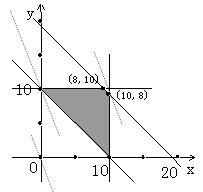
作出其可行域如图：

作直线l₀：5 x +3 y＝０，

再作直线l₀的平行直线l： 5 x +3 y＝Ｔ

当直线l经过点（０，10）时，Ｔ取得最小值，

当直线l经过点（10，8）时，Ｔ取得最大值，

所以，当x =10，y =8时，W_min=9800（元）

　　　当x =0，y =10时，W_max=14200（元）．

答：Ｗ的最大值为14200元，最小值为9800元．

20．（14分）

分析：将已知数据列成下表：

产品	甲种棉纱 （1吨）	乙种棉纱 （1吨）	资源限额 （吨）
一级子棉（吨）	2	1	300
二级子棉（吨）	1	2	250
利 润（元）	600	900

解：设生产甲、乙两种棉纱分别为x吨、y吨，利润总额为z元，

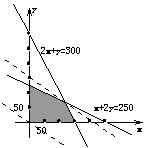那么

z=600x+900y．

作出以上不等式组所表示的平面区域(如图)，即可行域．

作直线l：600x+900y=0，即直线l：2x+3y=0,把直线l向右上方平移至l₁的位置时，直线经过可行域上的点M，且与原点距离最大，此时z=600x+900y取最大值．解方程组

,得M的坐标为x=≈117，y=≈67．

答：应生产甲种棉纱117吨，乙种棉纱67吨，能使利润总额达到最大．