高二数学几何概型能力形成单元测试卷

高二数学几何概型能力形成单元测试卷

（必修3　 3.2 几何概型）

班别　　　　 姓名　　　　  学号　　　　 成绩　　　　 

一、选择题

1. 取一根长度为3 m的绳子，拉直后在任意位置剪断，那么剪得两段的长都不小于1 m的概率是.

A.　　　　　 B.　　　　　 C.　　　　　 D.不确定

2. 已知地铁列车每10 min一班，在车站停1 min.则乘客到达站台立即乘上车的概率是

A.　　　　　 B.　　　　　 C.　　　　  D.

3. 在1万 km²的海域中有40 km²的大陆架贮藏着石油，假如在海域中任意一点钻探，钻到油层面的概率是.

A.　　　　　B.　　　　 C.　　　　 D.

二、填空题

1. 如下图，在一个边长为3 cm的正方形内部画一个边长为2 cm的正方形，向大正方形内随机投点，则所投的点落入小正方形内的概率是________.

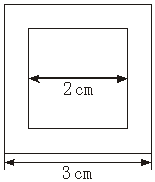
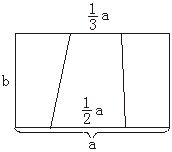
2. 如下图，在一个边长为a、b（a＞b＞0）的矩形内画一个梯形，梯形上、下底分别为a与a，高为b，向该矩形内随机投一点，则所投的点落在梯形内部的概率为________.

3. 两根相距6 m的木杆上系一根绳子，并在绳子上挂一盏灯，则灯与两端距离都大于2 m的概率是________.

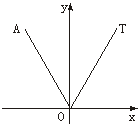
4. 如下图，在直角坐标系内，射线OT落在60°的终边上，任作一条射线OA，则射线落在∠xOT内的概率是________.

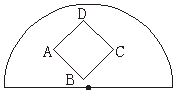
5. 如下图，在半径为1的半圆内，放置一个边长为的正方形ABCD，向半圆内任投一点，该点落在正方形内的概率为_________.

三、解答题

1. 在1 L高产小麦种子中混入了一粒带麦锈病的种子，从中随机取出10 mL，含有麦锈病种子的概率是多少？

2. 在等腰Rt△ABC中，在斜边AB上任取一点M，求AM的长小于AC的长的概率.

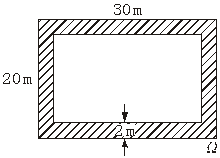
3. 一海豚在水池中自由游弋，水池为长30 m，宽20 m的长方形，求海豚嘴尖离岸边不超过2 m的概率.

4. 平面上画了一些彼此相距2a的平行线，把一枚半径r<a的硬币任意掷在这个平面上，求硬币不与任一条平行线相碰的概率.

参考答案

一、选择题

1. B　 2. A　　3. C

二、填空题

1. 　　2. 　 3. 　　4. 　　5.

三、解答题

1.  解：取出10 mL麦种，其中“含有病种子”这一事件记为A，

则P（A）= .

答：含有麦锈病种子的概率为.

2. 解：在AB上截取AC′=AC，于是P（AM＜AC）=P（AM＜）

=.

答：AM的长小于AC的长的概率为.

3.　解：对于几何概型，关键是要构造出随机事件对应的几何图形，利用图形的几何度量来求随机事件的概率.如下图，区域Ω是长30 m、宽20 m的长方形.图中阴影部分表示事件A：“海豚嘴尖离岸边不超过2 m”，问题可以理解为求海豚嘴尖出现在下图中阴影部分的概率.由于区域Ω的面积为30×20=600（m2），阴影A的面积为30×20－26×16=184（m2）

.∴P（A）=≈0.31.

4. 解：记事件A：“硬币不与任一条平行线相碰”.为了确定硬币的位置，由硬币中心O向靠得最近的平行线引垂线OM，垂足为M，参看下图，这样线段OM长度（记作OM）的取值范围是［0，a］，只有当r＜OM≤a时，硬币不与平行线相碰，所以P（A）=.