武汉中学高二下学期数学总复习试题(5)
武汉中学 柏任俊
一、选择题：
1. ABCD—A1B1C1D1是单位正方体，黑白两个蚂蚁从点A出发沿棱爬行，每走完一条棱称为“走完一段”。白蚂蚁爬行的路线是AA1→A1D1→…，黑蚂蚁爬行的路线是AB→BB1→…，它们都遵循如下规则：所爬行的第i＋2段与第i段所在直线必须是异面直线（其中i∈N＋），设两蚂蚁都走完第2003段后分别停在正方体的一个顶点处，则黑白蚂蚁的距离是 （ ）
A．1 B． C． D．0
2.将三棱锥P—ABC（如图甲），沿三条侧棱剪开后，展开成如图乙的形状，其中P1、B、P2共线，P2、C、P3共线，且P1P2 ＝ P2P3，则在三棱锥P—ABC中，PA与BC所成的角是（ ）
A．30° B．45°
C．60° D．90°
3.湖面上漂着一个球，湖面结冰后将球取出，冰面上留下一个圆面直径为24，深为8的穴，则该球的表面积为 （ ）
A．676
B．576 C．512 D．256
4.
的展开式中
的系数为
（ ）
A．
B．
C．
D．
5.如图,在杨辉三角中,斜线
的上方,从1开始
箭头所示的数组成一个锯齿形数列：
1,3,3,4,6,5,10,……，
记其前
项和为
,则
等于 （ ）
A．129 B．172
C．228 D．283
6.从－3, －2, －1, 0, 1, 2, 3, 4这8个数中任选3个不同的数组成二次函数y=ax2+bx+c的系数a, b, c, 则可确定坐标原点在抛物线内部的抛物线有 （ ）
A．72条 B．96条 C．128条 D．144条
7.设
＝ ， p ＝ (x1 －)2＋ (x2 －)2＋…＋ (xn －)2，
q ＝ (x1－ a)2＋ (x2 －a)2＋…＋ (xn －a)2，若 ≠a，则一定有
（ ）
A．p＞q B．p＝q C．p＜q D．与a的值有关
8.已知样本均值＝ 5，样本方差S2＝100，若将所有的样本观察值都乘以 后，则新的样本均值和样本标准差S′分别为 （ ）
A．1，4 B．1，2 C．5，4 D．25，2
9.设
为可导函数，且满足
，则过曲线
上点
处的切线率为
（ ）
A．2 B．-1 C．1 D．-2
10.函数
的图象如图所示，则
的值一定 （ ）
（A）等于0 （B）大于0
（C）小于0 （D）小于或等于
二、填空题：
11.已知四个面都是直角三角形的三棱锥，其中三个面展开后构成一个直角梯形ABCD，如图AD⊥AB，AD⊥DC，AB＝1，BC＝，CD＝2，则这个三棱锥的外接球的表面积是 （结果可含π）
12.设二项式
的展开式的各项系数的和为P，所有二项式系数的和为S，若P+S=272，则n等于
.
13.甲、乙两人玩猜数字游戏，先由甲心中任想一个数字，记为a，再由乙猜甲刚才想的数字，把乙猜的数字记为b,且a,b 
{0，1，2，…..,9},若a
b 
1,则称甲乙”心有灵犀”.现任意找两个人玩这个游戏,得出他们”心有灵犀”的概率为
.
14.某招呼站，每天均有三辆开往省城南京的分为上、中、下等级的客车。某天袁先生准备在该招呼站乘车前往南京办事，但他不知道客车的车况，也不知道发车的顺序。为了尽可能乘上上等车，他采取如下策略：先放过第一辆，如果第二辆好则上第二辆，否则上第三辆。那么他乘上上等车的概率为 .
15.已知函数
，则
16.设函数 f(x)＝x3＋ax2＋2bx＋c．若当 x∈（0，1）时，f(x)取得极大值；x∈（1，2）时，f(x)取得极小值，则 的取值范围是 ．
三、解答题：
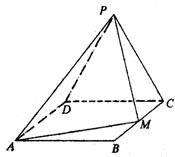
17.如图，边长为2的等边△PCD所在的平面垂直于矩形ABCD所在的平面，BC=
，M为BC的中点，（1）证明：AM⊥PM；（2）求二面角P—AM—D的大小；（3）求点D到平面AMP的距离.
|
18.三棱柱ABC—A1B1C1中，AB⊥BC，四边形BCC1B1是矩形，四边形A1ABB1是菱形且∠A1AB=60°，BC=3，AB=4.（Ⅰ）求证：平面A1BC⊥平面A1ABB1；（Ⅱ）求直线A1C与平面BCC1B1所成角的正切；（Ⅲ）求二面角C1－A1B－A的大小．
19.已知某种从太空飞船中带回的植物种子每粒成功发芽的概率都为
，某植物研究所分两个小组分别独立开展该种子的发芽实验，每次实验种一粒种子，假定某次实验种子发芽则称该次实验是成功的，如果种子没有发芽，则称该次实验是失败的．（1） 第一小组做了三次实验，求至少两次实验成功的概率；（2)）第二小组进行试验，到成功了4次为止，求在第四次成功之前共有三次失败，且恰有两次连续失败的概率．
20.某篮球职业联赛总决赛在甲、乙两支球队之间进行，比赛采用五局三胜制，即哪个队先胜三场即可获得总冠军。已知在每一场比赛中，甲队获胜的概率均为
，乙队获胜的概率均为
.求：（I）甲队以3：0获胜的概率；（II）甲队获得总冠军的概率。
21.函数
的图象上有两点A（0，1）和B（1，0）.
（Ⅰ）在区间（0，1）内，求实数a使得函数
的图象在x=a处的切线平行于直线AB；（Ⅱ）设m>0，记M（m，
），求证在区间（0，m）内至少有一实数b，使得函数图象在x=b处的切线平行于直线AM.
参考答案：
BDABD DCBBB 11.【答案】
；12.【答案】4；13.【答案】
；
14.【答案】（列举法）概率P ＝＝0.5；15.【答案】
；
16.【答案】（，1）. f´(x)＝ x2＋ax＋2b，令f´(x)＝0，由条件知，上述方程应满足：一根在（0，1）之间，另一根在（1，2）之间，∴ ，得 ，在aob坐标系中，作出上述区域如图所示，而 的意义是过两点P(a，b)与A(1，2)的直线斜率，
而P(a，b)在区域内，由图易知kPA∈（，1）．
17.解法1：（1）取CD的中点E，连结PE、EM、EA
∵△PCD为正三角形 ∴PE⊥CD，PE=PDsin∠PDE=2sin60°=
∵平面PCD⊥平面ABCD ∴PE⊥平面ABCD
∵四边形ABCD是矩形 ∴△ADE、△ECM、△ABM均为直角三角形
由勾股定理可求得EM=，AM=
，AE=3 .∴EM2+AM2=AE2,∴∠AME=90°, ∴AM⊥PM.
（2）由（1）可知EM⊥AM，PM⊥AM ∴∠PME是二面角P—AM—D的平面角
∴tan∠PME=
∴∠PMA=45°
∴二面角P—AM—D为45°
（3）设D点到平面PAM的距离为d，连结DM，则
在Rt△PEM中，由勾股定理可求得PM=，
，
|
. 即点D到平面PAM的距离为
.
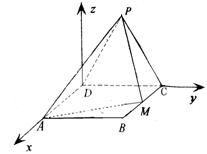
解法2：（1）以D点为原点，
分别以直线DA、DC
为x轴、y轴，建立
如图所示的空间直角
坐标系D—xyz，
依题意，可得D（0，0，0），P（0，1，），C（0，2，0），A（2
，0，0），
M（，2，0），
即
，∴AM⊥PM.
（2）设
平面PAM，则
取y=1，得
显然
平面ABCD，
.结合图形可知，二面角P—AM—D为45°；
（3）设点D到平面PAM的距离为d，由（2）可知
）与平面PAM垂直，
则
即点D到平面PAM的距离为
18.证明：（1）∵BC⊥AB，BC⊥BB1，∴BC⊥平面AA1B1B.∴平面A1BC⊥平面A1ABB1.
（2）作A1D⊥B1B于D，由（1）知平面BB1C1C⊥平面AA1B1B.
∴A1D⊥平面BB1C1C，连接DC，∴∠A1CD为直线A1C与平面BCC1B1所成角.
∵四边形A1ABB1是菱形则且∠A1AB=60°，
∴A1D=2，且D为BB1为中点，又BC=3，∴CD=
.∴tan∠A1CD=
∴直线A1C与平面BCC1B1所成角的正切为
(3)π－acrtan
19.解：（1）第一小组做了三次实验，至少两次实验成功的概率是
．
(2) 第二小组在第4次成功前，共进行了6次试验，其中三次成功三次失败，且恰有两次连续失败，其各种可能的情况种数为
．因此所求的概率为
．
20.解：（I）设“甲队以3：0获胜”为事件A，则
（II）设“甲队获得总冠军”为事件B，
则事件B包括以下结果：3：0；3：1；3：2三种情况
若以3：0胜，则
；
若以3：1胜，则
若以3：2胜，则
所以，甲队获得总冠军的概率为
21.（Ⅰ）解：直线AB斜率kAB=－1 
令
，解得 
（Ⅱ）证明：直线AM斜率 
考察关于b的方程
,即3b2－2b－m2+m=0
在区间（0，m）内的根的情况,
令g(b)= 3b2－2b－m2+m，则此二次函数图象的对称轴为
而
g(0)=－m2+m=m(1－m)，g(m)=2m2－m = m (2m－1)
∴（1）当
内有一实根
（2）当
内有一实根
（3）当
内有一实根
综上，方程g(b)=0在区间（0，m）内至少有一实根，故在区间（0，m）内至少有一实数b，使得函数图象在x=b处的切线平行于直线AM .