江苏省前黄高中2005~2006年度高二年级上学期期末考试
数 学 试 题
2006.1.22
命题人:
本试卷分选择题、填空题及解答题三部分,全卷满分150分,考试时间120分钟.
请考生把选择题的答案填涂到答题卡上,填空题及解答题统一做在答卷纸上。
一、选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题意要求的。
1.双曲线![]() 的左焦点到其渐近线的距离是
的左焦点到其渐近线的距离是
A.![]() B.
B.![]() C.1 D.
C.1 D.![]()
2.一动圆与圆![]() 及圆
及圆![]() 都内切,则动圆圆心的轨迹是
都内切,则动圆圆心的轨迹是
A.椭圆 B.双曲线 C.抛物线 D.圆
3.在正方体![]() 中,表面的对角线中与
中,表面的对角线中与![]() 成
成![]() 的有
的有
A.4条 B.6条 C.8条 D.10条
4.若一个![]() ,采用斜二测画法作出其直观图是面积等于1的
,采用斜二测画法作出其直观图是面积等于1的![]() ,则原
,则原![]() 的面积是
的面积是
A.![]() B.
B.![]() D.
D.![]()
5.当![]() 且
且![]() 时,曲线
时,曲线![]() 与曲线
与曲线![]() 的
的
A.焦距相等 B.准线相同 C.焦点相同 D.离心率相等
6.在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 上异于坐标原点
上异于坐标原点![]() 的两不同点
的两不同点![]() 满足
满足![]() ,则直线
,则直线![]() 必过定点
必过定点
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.若实数![]() 满足
满足![]() ,则
,则![]() 的最小值是
的最小值是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.已知点![]() ,
,![]() 是双曲线
是双曲线![]() 的右焦点,若双曲线上有一点
的右焦点,若双曲线上有一点![]() ,使
,使![]() 最小,则点
最小,则点![]() 的坐标为
的坐标为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.过抛物线![]() 的焦点
的焦点![]() 的直线与抛物线相交于
的直线与抛物线相交于![]() 两点,自
两点,自![]() 向准线作垂线,垂足分别为
向准线作垂线,垂足分别为![]() 、
、![]() ,则焦点
,则焦点![]() 与以线段
与以线段![]() 为直径的圆
为直径的圆![]() 之间的位置关系是
之间的位置关系是
A.焦点![]() 在圆
在圆![]() 上 B.焦点
上 B.焦点![]() 在圆
在圆![]() 内
内
C.焦点![]() 在圆
在圆![]() 外 D.随直线
外 D.随直线![]() 的位置改变而改变
的位置改变而改变
10.已知![]() 是直线,
是直线,![]() 是平面,给出下列四个命题:
是平面,给出下列四个命题:
(1)若![]() 垂直于
垂直于![]() 内的两条直线,则
内的两条直线,则![]() ;
;
(2)若![]() ,则
,则![]() ;
;
(3)若![]() ,则
,则![]() 平行于
平行于![]() 内的所有直线;
内的所有直线;
(4)若![]() 且
且![]() 则
则![]() .
.
 其中正确命题的个数是
其中正确命题的个数是
A.0 B.
11.如图,已知![]() 与
与![]() 是异面直线,且
是异面直线,且![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() 与
与![]() 所成的角为
所成的角为
 A.
A.![]() B.
B.![]()
C.![]() D.
D.![]()
12.如图,在正方体ABCD-A1B1C1D1中,点E、F分别在A1D、AC上,且A1E=2ED,CF=2FA,则EF与BD1的位置关系是
A.相交但不垂直 B.相交且垂直
C.异面 D.平行
二、填空题:本大题共6小题,每小题4分,共24分。
13.已知![]() 、
、![]() 、
、![]() 三点共线,则
三点共线,则![]() ▲ .
▲ .
14.若实数![]() 满足
满足 ,则
,则![]() 的最大值是 ▲ .
的最大值是 ▲ .
15.椭圆![]() 中过P(1,1)的弦恰好被P点平分,则此弦所在直线的方程是 ▲ .
中过P(1,1)的弦恰好被P点平分,则此弦所在直线的方程是 ▲ .
16.已知平行六面体![]() ,且
,且![]() ,
,![]() ,
,![]() ,若点
,若点![]() 是侧面
是侧面![]() 的中心,
的中心,![]()
![]() ,则
,则![]() ▲ .
▲ .
17.已知椭圆![]() 与双曲线
与双曲线![]() 具有相同的焦点F1,F2,设两曲线的一个交点为
具有相同的焦点F1,F2,设两曲线的一个交点为![]() ,
,![]() ,则双曲线的离心率为 ▲ .
,则双曲线的离心率为 ▲ .
18.若关于![]() 的方程
的方程![]() 没有实数解,则实数
没有实数解,则实数![]() 的取值范围为 ▲ .
的取值范围为 ▲ .
江苏省前黄高中2005~2006年度高二年级上学期期末考试
数 学 答 卷 纸
二、填空题
13. 14.
15. 16.
17. 18.
三、解答题
19.(本小题满分12分,每小题满分6分)
已知圆![]() :
:![]() ,直线
,直线![]() :
:![]() .
.
(1)求证:不论![]() 取何实数,直线
取何实数,直线![]() 恒过一个定点;
恒过一个定点;
(2)求直线![]() 被圆
被圆![]() 截得的弦长最小时,直线
截得的弦长最小时,直线![]() 的方程.
的方程.

20.(本小题满分12分,每小题满分6分)
如图,已知边长都为1正方形![]() 与正方形
与正方形![]() ,
,![]() ,
,![]() 分别是对角线
分别是对角线![]() 和
和![]() 上的点,且
上的点,且![]() .
.
(1)求证:![]() 平面
平面![]() ;
;
(2)求![]() 的最小值.
的最小值.
 21.(本小题满分14分,第一小题满分4分,第二、第三小题满分各5分)
21.(本小题满分14分,第一小题满分4分,第二、第三小题满分各5分)
如图,在棱长为1的正方体![]() 中,
中,![]() 分别为
分别为![]() 、
、![]() 、
、![]() 的中点.
的中点.
(1)求异面直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(2)求证:![]() 平面
平面![]() ;
;
(3)试在棱![]() 上找一点
上找一点![]() ,使
,使![]() ⊥平面
⊥平面![]() ,并证明你的结论.
,并证明你的结论.
22.(本小题满分14分,第一小题满分6分,第二小题满分8分)
已知双曲线![]() 的右焦点为
的右焦点为![]() ,过点
,过点![]() 作直线
作直线![]() 垂直于该双曲线的一条渐近线
垂直于该双曲线的一条渐近线![]() 于
于![]() .
.
(1)求该双曲线的方程;
(2)过点![]() 作直线
作直线![]() 交该双曲线于
交该双曲线于![]() 两点,如果
两点,如果![]() ,求直线
,求直线![]() 的方程.
的方程.
23.(本小题满分14分,前三小题满分各4分,第四小题满分2分)
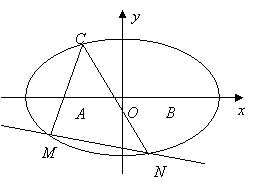
如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,一曲线
,一曲线![]() 过点
过点![]() ,且曲线
,且曲线![]() 上任一点到
上任一点到![]() 两点的距离之和不变.
两点的距离之和不变.
(1)建立适当的坐标系,求曲线![]() 的方程;
的方程;
(2)设点![]() 是曲线
是曲线![]() 上的一动点,求线段
上的一动点,求线段![]() 中点的轨迹方程;
中点的轨迹方程;
(3)设![]() 是曲线
是曲线![]() 上不同的两点,直线
上不同的两点,直线![]() 和
和![]() 的倾斜角互补,试判断直线
的倾斜角互补,试判断直线![]() 的斜率是否为定值。如果是,求这个定值;如果不是,请说明理由.
的斜率是否为定值。如果是,求这个定值;如果不是,请说明理由.
(4)若点![]() 是曲线
是曲线![]() 上的任一定点(除曲线
上的任一定点(除曲线![]() 与直线
与直线![]() 的交点),
的交点),![]() 是曲线
是曲线![]() 上不同的两点,直线
上不同的两点,直线![]() 和
和![]() 的倾斜角互补,直线
的倾斜角互补,直线![]() 的斜率是否为定值呢?如果是,请你指出这个定值。(本小题不必写出解答过程)
的斜率是否为定值呢?如果是,请你指出这个定值。(本小题不必写出解答过程)
 |
江苏省前黄高中2005~2006年度高二年级上学期期末考试
数 学 参 考 答 案
一、选择题(每小题5分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | C | A | C | D | A | B | D | B | A | B | C | D |
二、填空题(每小题4分)
13.5 14.12 15.![]()
16.2 17.![]() 18.
18.![]()
三、解答题
19.
解:(1)把直线![]() 方程整理为:
方程整理为:![]() [3分]
[3分]
令![]()
故不论![]() 取何实数,直线
取何实数,直线![]() 过定点P(3,1) [6分]
过定点P(3,1) [6分]
(2)由于直线![]() 过定点P(3,1)在圆
过定点P(3,1)在圆![]() 内,故当直线
内,故当直线![]() 垂直于PC时,直线
垂直于PC时,直线![]() 被圆
被圆![]() 截得的弦长最小。 [8分]
截得的弦长最小。 [8分]
∵![]() ,∴
,∴![]() [10分]
[10分]
 ∴直线
∴直线![]() 的方程是
的方程是![]()
![]() ,即
,即![]() [12分]
[12分]
20.
(1)证明:过![]() 作
作![]() ,垂足为
,垂足为![]() ,连结
,连结![]() 。
。
∵![]() ,又
,又![]()
∴![]() [2分]
[2分]
∴![]()
∴平面![]() 平面
平面![]() [4分]
[4分]
从而![]() 平面
平面![]() [6分]
[6分]
(2)![]()
![]() [8分]
[8分]
由勾股定理知:![]() [10分]
[10分]
当![]() 时,
时,![]() 的最小值为
的最小值为![]() 。 [12分]
。 [12分]
21.
解:(1)以![]() 为坐标原点,
为坐标原点,![]() 分别作为
分别作为![]() 轴,
轴,![]() 轴和
轴和![]() 轴建立空间直角坐标系,则
轴建立空间直角坐标系,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() [1分]
[1分]
∴![]() ,
,![]() [2分]
[2分]
∴
故异面直线![]() 与
与![]() 所成角的余弦值为
所成角的余弦值为![]() [4分]
[4分]
(2)∵![]() ,
,![]() [5分]
[5分]
而![]() , ∴
, ∴![]() [7分]
[7分]
故![]() 与平面
与平面![]() 共面,又
共面,又![]() 不在平面
不在平面![]() 内
内
∴![]() 平面
平面![]() [9分]
[9分]
(3)设![]() ,则
,则![]()
由![]() [11分]
[11分]
∴![]() [13分]
[13分]
![]() 为棱
为棱![]() 的中点时,
的中点时,![]() ⊥平面
⊥平面![]() 。 [14分]
。 [14分]
注:此题直接取![]() 的中点也可以较方便地解决前两小题,第三小题可用三垂线定理解决。
的中点也可以较方便地解决前两小题,第三小题可用三垂线定理解决。
22.
(1)设F(c,0),![]() [1分]
[1分]
解方程组 得
得![]() [3分]
[3分]
又已知![]()
![]() [5分]
[5分]
∴双曲线方程为![]() [6分]
[6分]
(2)若直线![]() 过右焦点为F(
过右焦点为F(![]() ),可设直线
),可设直线![]() 的方程为
的方程为![]() 代入
代入![]() ,
,
得![]() [8分]
[8分]
设![]()
则![]() [9分]
[9分]
∴
故 [11分]
[11分]
∴
解得:![]() 或
或![]() [13分]
[13分]
∴所求直线![]() 的方程为
的方程为![]() 和
和![]() [14分]
[14分]
(若遗漏![]() 则扣3分)
则扣3分)
 23.解:以
23.解:以![]() 的中点为原点,
的中点为原点,![]() 所在直线为
所在直线为![]() 轴建立直角坐标系。
轴建立直角坐标系。
∵![]() [1分]
[1分]
不难知道:曲线![]() 是以
是以![]() 为两焦点、长轴长为4的椭圆。 [3分]
为两焦点、长轴长为4的椭圆。 [3分]
故曲线![]() 的方程为
的方程为![]() [4分]
[4分]
(2)设线段![]() 的中点为
的中点为![]() ,∵
,∵![]() ,∴
,∴![]() [5分]
[5分]
∵点![]() 在曲线
在曲线![]() 上,故可得:
上,故可得:![]() [7分]
[7分]
即线段![]() 中点的轨迹方程为
中点的轨迹方程为![]() [8分]
[8分]
(3)设直线![]() 和
和![]() 的斜率分别为
的斜率分别为![]()
直线![]() 的直线方程为
的直线方程为![]()
代入曲线![]() 的方程,得
的方程,得
![]() [9分]
[9分]
 由韦达定理:
由韦达定理:![]() ,
,
∴![]()
同理![]() [10分]
[10分]
而![]() ,
,![]()
∴
故直线![]() 的斜率为定值
的斜率为定值![]() [12分]
[12分]
(4)设![]() ,则直线
,则直线![]() 的斜率为定值
的斜率为定值![]() [14分]
[14分]
(第四小题可用极限情形来考虑:当直线![]() 和
和![]() 的倾斜角都为
的倾斜角都为![]() 时,直线
时,直线![]() 即为
即为![]() 处的切线)
处的切线)
命题人:张国良 李学富