江苏省西亭高级中学高二数学期末测试卷
第Ⅰ卷(选择题共60分)
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有
一项是符合题目要求的。
1. .动圆的圆心在抛物线![]() 上,且动圆恒与直线
上,且动圆恒与直线![]() 相切,则动圆必经过定点()
相切,则动圆必经过定点()
 (A)
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
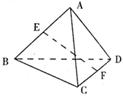
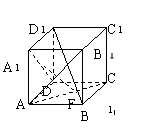
2. 如图,正方体ABCD-A![]() B
B![]() C
C![]() D
D![]() 中,EF是异面直线AC和A
中,EF是异面直线AC和A![]() D的公垂线,则EF和BD
D的公垂线,则EF和BD![]() 关系是( )
关系是( )
A.相交不垂直 B.相交垂直
C.异面直线 D.互相平行
3.下列命题正确的是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
4.过点M(-2,4)作圆C:![]() 的切线l,直线
的切线l,直线![]()
与l平行,则l1与l之间的距离是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
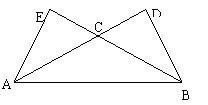 5. 如图,在△ABC中,∠CAB=∠CBA=30°,AC、BC边上的高分别为BD、AE,则以A、B为焦点,且过D、E的椭圆与双曲线的离心率的倒数和为
( )
5. 如图,在△ABC中,∠CAB=∠CBA=30°,AC、BC边上的高分别为BD、AE,则以A、B为焦点,且过D、E的椭圆与双曲线的离心率的倒数和为
( )
A.![]() B.
B.![]() D.
D.![]()
6.直线![]() 在
在![]() 轴上截距为
轴上截距为![]() ,且它的倾斜角是直线
,且它的倾斜角是直线![]() 的倾斜角的
的倾斜角的![]() 倍,则
倍,则![]() 的值分别为: ( )
的值分别为: ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.若双曲线的一个顶点到两条准线的距离和等于4,一个焦点到两条渐近线的距离和等于8,
则双曲线的离心率的值是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.设坐标原点为O,抛物线![]() 与过焦点的直线交于A、B两点,则
与过焦点的直线交于A、B两点,则![]() 的值是
的值是
( )
A.![]() B.
B.![]() C.3 D.-3
C.3 D.-3
9.![]() 是异面直线,
是异面直线,![]() 表示平面,
表示平面,![]() 甲:
甲:![]() 乙:
乙:![]() ,则甲是乙的( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.不充分不必要条件
,则甲是乙的( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.不充分不必要条件
10.过椭圆![]() 的一个焦点F作弦AB,若
的一个焦点F作弦AB,若![]() ,
,![]() ,则
,则![]() 的数值为 ( )
的数值为 ( )
A.![]() B.
B.![]() C.
C.![]() D.与a、b斜率有关
D.与a、b斜率有关
11.已知F1、F2是两个定点,点P是以F1和F2为公共焦点的椭圆和双曲线的一个交点,并
且PF1⊥PF2,e1和e2分别是椭圆和双曲线的离心率,则有 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12. 对于抛物线 y2 =4x上任意一点Q,点P ( a, 0 )都满足 PQ ≥ a ,则a的取值范围是
A. (-∞,0) B. (-∞,2 ] C. [ 0,2 ] D. (0,2)
二、填空题:本大题共6小题,每小题4分,共24分,把答案填在题中横线上
13. 已知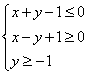 ,则函数
,则函数![]() 的最小值为
.
的最小值为
.
14.设中心在原点的椭圆与双曲线![]() 有公共焦点,且它们的离心率互为倒数,则该椭圆的方程是
;
有公共焦点,且它们的离心率互为倒数,则该椭圆的方程是
;
|
16.在空间四边形ABCD中,E、F分别为棱AB、CD的
中点,![]() 为EF与AC所成的角,
为EF与AC所成的角,![]() 为EF与BD所成
为EF与BD所成
的角,为使![]() ,须添加条件
.((必
,须添加条件
.((必
须写出两个答案)
17.已知椭圆![]() ( a > b > 0) 的离心率为
( a > b > 0) 的离心率为![]() ,准线为
,准线为![]() 、
、![]() ;双曲线
;双曲线![]() 离心率为
离心率为![]() ,准线为
,准线为![]() 、
、![]() ;;若
;;若![]() 、
、![]() 、
、![]() 、
、![]() 正好围成一个正方形,则
正好围成一个正方形,则![]() 等于 .
等于 .
18. 对于四面体ABCD,给出下列四个命题:①若AB=AC,BD=CD则BC⊥AD;②若AB=CD,AC=BD则BC⊥AD;③若AB⊥AC,BD⊥CD则BC⊥AD;④若AB⊥CD, BD⊥AC则BC⊥AD;其中真命题序号是 .
三、解答题:本大题共5小题,共66分,解答应写出文字说明、证明过程或演算步骤.
19.(本小题满分12分)
|
20.(12分)设F1、F2为椭圆 ![]() 的两个焦点,P为椭圆上的一点,已知P、F1、F2是一个直角三角形的三个顶点,且 PF1
> PF2 ,求
的两个焦点,P为椭圆上的一点,已知P、F1、F2是一个直角三角形的三个顶点,且 PF1
> PF2 ,求![]() 的值.
的值.
21.(本小题满分14分)已知抛物线![]() 的弦AB与直线
的弦AB与直线![]() 有公共点,且弦AB的中点N到
有公共点,且弦AB的中点N到![]() 轴的距离为1,求弦AB长度的最大值,并求此直线AB所在的直线的方程.
轴的距离为1,求弦AB长度的最大值,并求此直线AB所在的直线的方程.
22.(本小题14分)
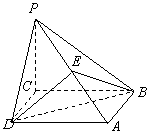 已知四棱锥P-ABCD的体积为
已知四棱锥P-ABCD的体积为![]() ,PC
,PC![]() 底面ABCD,
底面ABCD, ![]() ABC
ABC
和![]() ACD都是边长为1的等边三角形,点E分侧棱PA所成的
ACD都是边长为1的等边三角形,点E分侧棱PA所成的
比![]() .
.
(1)当![]() 为何值时,能使平面BDE
为何值时,能使平面BDE![]() 平面ABCD?并给出证明;
平面ABCD?并给出证明;
(2)当平面BDE![]() 平面ABCD时,求P点到平面BDE的距离;
平面ABCD时,求P点到平面BDE的距离;
(3)当![]() =1时,求二面角A-BE-D的大小.
=1时,求二面角A-BE-D的大小.
23.(本小题14分)
已知双曲线![]() 过点
过点![]() ,且它的渐近线方程是
,且它的渐近线方程是![]()
(1)
求双曲线![]() 的方程;
的方程;
(2)
设椭圆![]() 的中心在原点,它的短轴是双曲线
的中心在原点,它的短轴是双曲线![]() 的实轴,且
的实轴,且![]() 中斜率为
中斜率为![]() 的弦的中点轨迹恰好是
的弦的中点轨迹恰好是![]() 的一条渐近线截在
的一条渐近线截在![]() 内的部分,试求椭圆
内的部分,试求椭圆![]() 的方程.
的方程.
2005—2005学年度第一学期期末
高二数学试卷参考答案
一、选择题1—6:BBBCAB 7—12:CABBDA
二、填空题13.![]() 14.
14.![]() 15.
15.![]() 16.
16.![]() ;AB=AD CB=CD(若其它正确答案) 17.
;AB=AD CB=CD(若其它正确答案) 17.![]() ,18.①③
,18.①③
三、解答题:
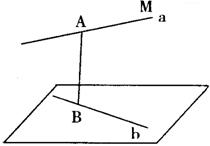
17.解:设过B点与a平行的直线为c、b、c所确定 的平面为α.由于AB是异面直线a、b的公垂线
的平面为α.由于AB是异面直线a、b的公垂线
![]() …………2分
…………2分
过点M作MN⊥c垂足为N,则AB//MN
![]() ,四边形ABMN是矩形
,四边形ABMN是矩形
![]()
在α内过N作NC⊥b,垂足为C,连MC,由三垂线定理知MC⊥b
∴MC即为点M到b的距离………………7分
又a、b所成的角为![]() ………………9分
………………9分
在Rt△BCN中,![]()
![]() …………12分
…………12分
18.解: 设组装![]() 件
件![]() 产品,
产品,![]() 件
件![]() 产品,利润为
产品,利润为![]() 万元
万元
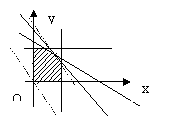 由题意得 目标函数:
由题意得 目标函数: ![]() 2分
2分
约束条件: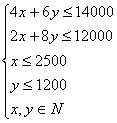 6分
6分
作出可行域 10分
作出直线![]() ,平移
,平移![]() 到点A处
到点A处![]() 取最大值;
取最大值;
由![]() 得
得![]()
![]() 最优解为
最优解为![]() 11分
11分
![]() 当组装2000件X产品,1000件Y产品时,该月利润最高,最高是400万元. 12分
当组装2000件X产品,1000件Y产品时,该月利润最高,最高是400万元. 12分
19.解: (1)设原点O关于L:![]() 的对称点
的对称点![]() ,则
,则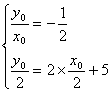
![]() 的方程
的方程![]() …………4分
…………4分
(2)设![]()
又![]() ,………………6分
,………………6分
由![]() …………8分
…………8分
又 消去
消去![]() …………10分
…………10分
![]()
|
20.解:设![]() 、
、![]() ,中点
,中点![]()
当AB直线的倾斜角90°时,AB直线方程是![]() (2分)
(2分)
当AB直线的倾斜角不为90°时,![]() 相减得
相减得![]()
所以![]() (4分)
(4分)
设AB直线方程为:![]() ,由于弦AB与直线y=1有公共点,故当y=1时
,由于弦AB与直线y=1有公共点,故当y=1时
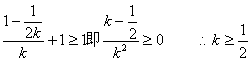 (6分)
(6分)
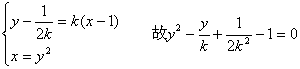
所以![]() ,故
,故
![]() (8分)
(8分)
![]()
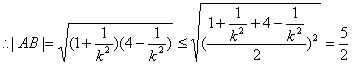
故当![]() (12分)
(12分)
22、解 (1)依题设,底面ABCD为菱形,设AC![]() BD=O,连结
BD=O,连结
OE,则OE⊥BD.若平面BDE⊥平面ABCD,则OE⊥平面ABCD,
∵CP⊥平面ABCD,∴OE‖CP.
∵O为AC中点,∴E为PA中点,且![]() .
.
(2)由(1)知,OE⊥平面ABCD,CP‖OE,CP‖平面BDE,
故P到平面BDE的距离即为C到平面BDE的距离,易证CO⊥
平面BDE,∴CO即为C到平面BDE的距离,
而CO=![]() AC=
AC=![]() ,
,
∴点P到平面BDE的距离为![]() .
.
说明 亦可化为求点A到平面BDE的距离.
(3)![]() 时,即有平面BDE⊥平面ABCD,交线为BD,∵AO⊥BD,AO
时,即有平面BDE⊥平面ABCD,交线为BD,∵AO⊥BD,AO![]() 平面ABCD,∴AO⊥平面BDE,过O作OQ⊥BE于Q,连结QA,则由三垂线定理知QA⊥BE,
平面ABCD,∴AO⊥平面BDE,过O作OQ⊥BE于Q,连结QA,则由三垂线定理知QA⊥BE,
∴∠AQO就是二面角A-BE-D的平面角.
在RtΔBOE中,∵OE=![]() PC=
PC=![]() ,OB=
,OB=![]() AB=
AB=![]() ,∴BE=
,∴BE=![]() ,
,
故由![]() 得,
得,![]() .
.
在RtΔAOQ中,![]() ,即二面角A-BE-D的大小为
,即二面角A-BE-D的大小为![]() .
.
22、(1)设双曲线![]() 的方程为
的方程为![]()
![]() 过点
过点![]()
![]()
![]()
双曲线![]() 的方程为
的方程为![]() 4分
4分
(2)由题意可设椭圆的方程为![]()
设斜率为-4的直线与椭圆交于点![]() ,
,![]() AB中点
AB中点![]() 则有
则有
![]() ①
①
![]() ②
②
①-②得 ![]()
![]() 8分
8分
![]()
![]() 10分
10分
又![]()
![]()
![]() 椭圆的方程为
椭圆的方程为![]() 14分
14分