双曲线解答题2
21、已知双曲线2x2-y2=2 , 试问过点N(1,1)能否作一直线与双曲线交于C,D两点, 且使N为CD的中点?这样的直线如果存在, 求出它的方程, 如果不存在, 则说明其理由.翰林汇
22、在双曲线![]() 的一支上的三点A(x1,y1)、B(
的一支上的三点A(x1,y1)、B(![]() ,6)、C(x2,y2)与焦点F(0,5)的距离成等差数列。(1)求y1+y2;(2)证明:线段AC的垂直平分线经过一定点。翰林汇
,6)、C(x2,y2)与焦点F(0,5)的距离成等差数列。(1)求y1+y2;(2)证明:线段AC的垂直平分线经过一定点。翰林汇
23、根据条件求圆锥曲线的离心率:
P为椭圆或双曲线上一点,焦点是F1和F2,且∠PF1F2=2![]() ,∠PF2F1=
,∠PF2F1=![]() .翰林汇
.翰林汇
24、根据条件求圆锥曲线的离心率:
双曲线的过焦点且垂直于实轴的弦与另一焦点组成等腰直角三角形.翰林汇
25、椭圆![]() 和双曲线
和双曲线![]() 的焦点在x轴上,它们的离心率是方程9x2-18x+8=0的两根,求m和n的值.
的焦点在x轴上,它们的离心率是方程9x2-18x+8=0的两根,求m和n的值.
翰林汇26、根据条件,求双曲线方程:对称轴是坐标轴,交圆x2+y2=17于点A(4,-1),一渐近线平行于圆过A点的切线.翰林汇
27、根据条件,求双曲线方程:对称轴是坐标轴,实轴长=虚轴长,通过点(3,1).
翰林汇28、已知双曲线的中心在原点,对称轴为坐标轴,离心率![]() ,一条准线的方程为
,一条准线的方程为![]() ,求此双曲线的标准方程.翰林汇
,求此双曲线的标准方程.翰林汇
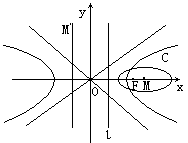
29、已知点F与直线l分别是双曲线x2-3y2=3的右焦点与右准线, 以F为左焦点 , l为左准线的椭圆C的中心为M,
又M关于直线y=2x的对称点M′恰好在已知双曲线的左准线上(如图),
求椭圆C的方程及其离心率.
 翰林汇
翰林汇
30、双曲线b2x2-a2y2=a2b2(a>0,b>0)的右焦点为F,过F的直线交双曲线于两点A、B,线段AB的中垂线交x轴于点E,试求![]() 的值.
的值.
翰林汇31、给定椭圆![]() ,求与这个椭圆有公共焦点的双曲线,使得以它们的交点为顶点的四边形面积最大,并求出相应四边形在第一象限内的顶点坐标.翰林汇
,求与这个椭圆有公共焦点的双曲线,使得以它们的交点为顶点的四边形面积最大,并求出相应四边形在第一象限内的顶点坐标.翰林汇
32、直线l过双曲线x2-4y2=4的右焦点F2,且与双曲线的右支交于两点A、B,A、B与双曲线左焦点F1的距离为d1、d2,试求d1d2的最小值.翰林汇
33、双曲线b2x2-a2y2=a2b2(a>0,b>0)上的一点M,到左、右焦点的距离分别为![]() ,到双曲线中心的距离为
,到双曲线中心的距离为![]() ,当点M在右支上运动时,求
,当点M在右支上运动时,求![]() 的最大值.翰林汇
的最大值.翰林汇
34、双曲线中点在原点,准线平行x轴,离心率为![]() ,若点P(0,5)到双曲线上的点的距离的最小值是2时,求双曲线的方程.翰林汇
,若点P(0,5)到双曲线上的点的距离的最小值是2时,求双曲线的方程.翰林汇
35、求与双曲线x2-2y2=2有共同的渐近线,且经过点(2,-2)的双曲线方程.
翰林汇36、过双曲线4x2-y2=20的焦点,作垂直于实轴的弦PQ,求![]()
翰林汇37、用直尺和圆规作点画出下列方程的曲线:(1)16x2-9y2=144;(2)y2-4x2=64.翰林汇
38、在相距1000米的A、B两地,听到发炮声的时间差为2秒,已知声速是340米/秒.炮位在怎样的曲线上?翰林汇
39、已知点M到定点A(0,-2![]() )与到定直线
)与到定直线![]() 的距离之比等于
的距离之比等于![]() ,求点M的轨迹.翰林汇
,求点M的轨迹.翰林汇
40、已知一双曲线与椭圆25x2+9y2=225的焦点相同,且它们的离心率之和等于
2.8,求此双曲线方程.
双曲线解答题2 〈参考答案〉
21、 不存在.翰林汇
22、 (1)∵ey1-a+ey2-a=26e-a,∴y1+y2=12;
(2)设AC的垂直平分线DE的方程为y=k(x-![]() ,
,
![]()
![]() .
.
又![]() y1+y2=12,k=-
y1+y2=12,k=-![]() ,∴x1+x2=13(-
,∴x1+x2=13(-![]() ),∴DE:y=kx+
),∴DE:y=kx+![]() ,故DE过定点(0,
,故DE过定点(0,![]() ).翰林汇
).翰林汇
23、 椭圆:2cos![]() -1;双曲线:2cos
-1;双曲线:2cos![]() +1.翰林汇
+1.翰林汇
24、 ![]() +1 翰林汇25、 m=5,n=7.翰林汇 26、
+1 翰林汇25、 m=5,n=7.翰林汇 26、 ![]() 翰林汇
翰林汇
27、 x2-y2=8翰林汇
28、 解: 由题设, 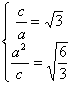 解得
解得 ![]() .
.
∴双曲线方程为 ![]() .
.
翰林汇29、 ∵ F(2,0) ![]() , 再设P(x,y)在C上, 则由
, 再设P(x,y)在C上, 则由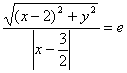 , 得(1-e2)x2+y2+(3e2-4)x+4-
, 得(1-e2)x2+y2+(3e2-4)x+4-![]() e2=0, 于是中心为
e2=0, 于是中心为![]()
由条件得方程为x2+2y2-5x+![]() =0, 即4x2+8y2-20x+23=0,
离心率
=0, 即4x2+8y2-20x+23=0,
离心率![]()
翰林汇
30、 ![]() 即
即![]() 翰林汇 31、 y2-x2=
翰林汇 31、 y2-x2=![]() (a2-b2),(
(a2-b2),(![]() 翰林汇
翰林汇
32、 d1d2的最小值为![]() 翰林汇 33、 最大值为
翰林汇 33、 最大值为![]() 即e)翰林汇
即e)翰林汇
34、 设双曲线方程![]() ;M(x,y)为双曲线上任意一点.
;M(x,y)为双曲线上任意一点.
由![]() ,∴
,∴![]() ,∴b2=c2-a2=
,∴b2=c2-a2=![]() .
.
而PM2=x2+(y-5)2=![]() (y-4)2+5-a2.
(y-4)2+5-a2.
以下分a≤4或a>4讨论,得双曲线方程![]() .翰林汇
.翰林汇
35、 2y2-x=4翰林汇
36、 8![]() 翰林汇
37、 略翰林汇
翰林汇
37、 略翰林汇
38、 ![]() (以AB的中点为原点,AB所在直线为x轴)翰林汇
(以AB的中点为原点,AB所在直线为x轴)翰林汇
39、 等轴双曲线y2-x2=4翰林汇 40、 3y2-x2=12