湖北省部分重点高中2006年春季期中联考
高二年级数学试题
命(审)题学校:阳新一中 命题人:宋晓舟 审题人:徐卫国 李儒斌 陈绪全
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。第Ⅰ卷1至2页,第Ⅱ卷3至8页,满分150分,考试时间120分钟。
注意事项:
1.答题前,考生务必将自己的学校.姓名.考号.班级填写在试卷指定位置。
2.第Ⅰ卷答案写在第Ⅱ卷卷首答题栏内,第Ⅱ卷答案写在各题指定答题处。
第Ⅰ卷(选择题,共60分)
一.选择题(本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的,请将所选答案填在答题卷的指定的答题栏内)
1.若直线a和直线b都与直线c垂直,则a和b的位置关系是( )
A.平行 B.相交 C.异面 D.以上都有可能
2.已知向量![]() =(2,4,x),
=(2,4,x),![]() =(2,y,2),若
=(2,y,2),若![]() =6,
=6,![]() ⊥
⊥![]() ,则x+y的值是( )
,则x+y的值是( )
A.-3或1 B.3或
3.设a、b是两条异面直线,在下列命题中正确的是( )
A.有且仅有一条直线与a、b都垂直
B.有一平面与a、b都垂直
C.过直线a有且仅有一个平面与b平行
D.过空间中任一点必可作一条直线与a、b都相交
4.已知三棱锥P—ABC,下列条件中:
①PA=PB=PC; ②PA、PB、PC两两垂直; ③PA、PB、PC与底面ABC所成的角均相等。
④PA⊥BC,PB⊥AC
能推出点P在底面ABC上的射影为△ABC垂心的是( )
A.①② B.②③ C.②④ D.①④
5.在120°的二面角内,放置一个半径为3的球,该球切二面角的两个半平面于A、B两点,那么这两个切点在球面上的最短距离为( )
A.![]() B.π C.
2π D.
3π
B.π C.
2π D.
3π
6.棱柱成为直棱柱的一个必要但不充分条件是( )
A.棱柱有一条侧棱与底面垂直 B.棱柱有一条侧棱与底面的两条边垂直
C.棱柱有两个相邻的侧面互相垂直 D.棱柱有一个侧面与底面的一条边垂直
7.若![]() ⊥
⊥![]() ,
,![]() ⊥
⊥![]() ,
,![]() =α
=α![]() +β
+β![]() (α、β∈R),
(α、β∈R),![]() ∥
∥![]() ,
,![]() 与
与![]() 一定( )
一定( )
A.相交 B.共线 C. 垂直 D.以上都有可能
8.(文科)有四位教师在同一年级的4个班级中,各教一个班的数学,在数学考试时,要求每位教师均不在本班监考,则安排监考的方法总数是( )
A.8 B
(理科)七个人坐成一排,现要调换其中3个人中每一个人的位置,其余4个人的位置不变,则不同的调换方式有( )
A.![]() B
B![]() C.
C. ![]() D. 2
D. 2![]()
9.已知![]() ,
,![]() 是直线,
是直线,![]() 、
、![]() 、
、![]() 是平面,给出下列命题
是平面,给出下列命题
①![]() ∥
∥![]() ,
,![]() 和
和![]() ⊥
⊥![]() ,则
,则![]() ⊥
⊥![]() 且
且![]() ∥
∥![]()
②若![]() 且
且![]() ⊥
⊥![]() ,则
,则![]() ⊥
⊥![]() ③若
③若![]() ,
,![]() 且
且![]() ∥
∥![]() ,则
,则![]() ∥
∥![]()
④若![]() ∥
∥![]() ,
,![]() ,则
,则![]() ∥
∥![]()
其中正确命题的序号( )
A.②③ B.①② C.②④ D.①④
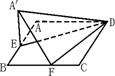 10.如图,正方形ABCD边长为4,E是AB的中点,F是BC边上的一个动点,将△ADE和△DCF分别沿DE、DF折起,使A、C重合于A′,则A′点到平面DEF的距离的最大值为( )
10.如图,正方形ABCD边长为4,E是AB的中点,F是BC边上的一个动点,将△ADE和△DCF分别沿DE、DF折起,使A、C重合于A′,则A′点到平面DEF的距离的最大值为( )
A.![]() B.
B.![]()
C. 2![]() D.
3
D.
3![]()
11.(文科作)正三棱锥P-ABC的侧棱长为a,各侧面三角形的顶角为30°,M、N为棱PB、PC上的动点,则△AMN周长的最小值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
(理科作)有一个正四棱锥,它的底面边长与侧棱长都为a,现有一张正方形包装纸将其完全包住,不能裁减,但可以折叠,那么包装纸的最小边长应为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.将一个四棱锥的每个顶点染上一种颜色,并使一条棱的两端异色,若只有4种颜色可供使用,则不同的染色方法种数为( )种
A.24 B.48 C. 60 D. 72
二.填空题(本大题共4小题,每小题4分,共16分)
13.某乒乓球队共有男女队员18人,现从中选出男女队员各一人组成一对双打组合,由于在男队员中有两人主攻单打项目,不参与双打组合,这样一共有64种组合方式,则乒乓球队中女队员的人数为 人。
14.考察下列三个命题,在“
”处都缺少一个条件,补上这个条件使其构成真命题(其中![]() 、m为直线,
、m为直线,![]() 为平面)则此条件为 。
为平面)则此条件为 。
![]()
![]()
![]() ①
①
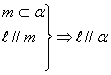 ②
②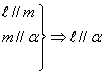 ③
③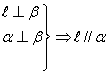
15.(文科)长方体的一个顶点上的三条棱分别是3,4,5,且它的八个顶点都在同一个球面上,这个球的表面积是 。
(理科)三棱锥A-BCD三个侧面两两垂直,底面BCD上一点P到三个侧面的距离分别为2,3,6,则P点到三棱锥顶点A的距离为 。
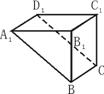 16.已知在长方体ABCD-A1B1C1D1中,A1B1=B1B=2,A1D1=1,沿该长方体的对角面A1D1CB切得一个几何体(如图),点P在△A1B1B面上运动,若点P到面B1C1CB的距离等于点P到棱A1D1的距离的
16.已知在长方体ABCD-A1B1C1D1中,A1B1=B1B=2,A1D1=1,沿该长方体的对角面A1D1CB切得一个几何体(如图),点P在△A1B1B面上运动,若点P到面B1C1CB的距离等于点P到棱A1D1的距离的![]() 倍,则点P到点B1的距离的最小值是
。
倍,则点P到点B1的距离的最小值是
。
三.解答题(本大题共6小题,共74分,将答案写出答题卷指定的答题栏内)
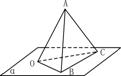 17.(12分)已知∠BOC在平面
17.(12分)已知∠BOC在平面![]() 内,OA是平面
内,OA是平面![]() 的斜线,∠AOB=∠AOC=60°,且OA=OB=OC=a,BC=
的斜线,∠AOB=∠AOC=60°,且OA=OB=OC=a,BC=![]() a,求OA与平面
a,求OA与平面![]() 所成的角。
所成的角。
 18.(12分)已知平行六面体ABCD-A1B1C1D1中,底面ABCD是边长为2且∠BAD=60°的菱形,∠A1AB=A1AD=45°,AA1=
18.(12分)已知平行六面体ABCD-A1B1C1D1中,底面ABCD是边长为2且∠BAD=60°的菱形,∠A1AB=A1AD=45°,AA1=![]()
(1)求对角线AC1的长
(2)直线BD1与AC夹角的余弦值
19.(12分)某中学三个年级各有十个编号从1到10的班级,为探索教书育人新方法,在全校学生中实施以“立志、立法、立德”为内容的“三立”教育工程。为此在三个年级中抽取14名学生组成第一期“三立”教育指导培训班,要求每个班级至多有一名学生参加,抽取方法是:高一任意抽取8名学生;高二按班级序号的奇偶性分两组各抽取二名;高三抽取2名学生且所抽的班级序号不得相邻,则培训班共有多少种不同的组成方案?
若指派五名教师到三个年级指导“三立”工程实施,要求每个年级至少一人,则有多少种不同的分配方案?
20.(12分)如图,在正三棱柱ABC-A1B1C1中,A1A=AB=a,G、E、F分别是A1C1、AB和BC的中点。
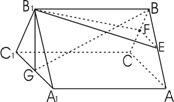 (1)(文科作)求证:EF⊥平面GB1B;
(1)(文科作)求证:EF⊥平面GB1B;
(理科作)求证:平面B1EF⊥平面GB1B;
(2)求点G到平面B1EF的距离。
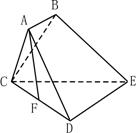 21.(12分)如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,三角形ACD是正三角形且AD=DE=2,AB=1,F是CD的中点。
21.(12分)如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,三角形ACD是正三角形且AD=DE=2,AB=1,F是CD的中点。
(1)求证:AF//平面BCE
(2)求二面角C-BE-D的正切值。
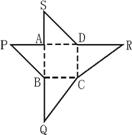 22.(14分)如图为某四棱锥的展开图,其中ABCD是边长为1的正方形,SA=PA=1,DR=SD,BQ=BP且点S、A、B、Q及P、A、D、R共线,沿图中虚线将它们折叠成四棱锥,使P、Q、R、S四点重合为S。
22.(14分)如图为某四棱锥的展开图,其中ABCD是边长为1的正方形,SA=PA=1,DR=SD,BQ=BP且点S、A、B、Q及P、A、D、R共线,沿图中虚线将它们折叠成四棱锥,使P、Q、R、S四点重合为S。
(1)请画出四棱锥S—ABCD的示意图,并证明SA⊥底面ABCD;
(2)设E为AB中点,证明:面SEC⊥面SCD;
(3)线段SC上是否存在一点k,使折叠后的空间图形中AK⊥平面SBD?
(4)(只理科作)由若干个这样的几何体不切割能否拼成一个正方体,若能,需要几个?若不能,说明理由。