惠州市第一中学高二数学必修5水平测试答案
一、选择题:(请将正确答案的代号填在答题卡内,每小题4分,共40分)
| 题 号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 得 分 |
| 答案 | C | A | C | B | C | A | B | D | C | A |
二、填空题:(每题4分,共16分)
11、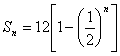 12、
12、![]() 13、等边三角形 14、
13、等边三角形 14、![]()
![]()
三.解答题(第15,16题每小题12分,第17,18题每小题10分共44分)
15、.(理科)解:(Ⅰ)由![]()
由b2=ac及正弦定理得 ![]()
于是![]()
![]()
(Ⅱ)由![]()
由余弦定理 b2=a2+c2-2ac+cosB 得a2+c2=b2+2ac·cosB=5.
![]()
(文科)解:由原不等式得: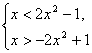 即
即 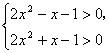 解得:
解得:
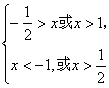 即:
即:![]() .
.
∴原不等式的解集为![]()
16、(理科)等差数列{an}不是常数列,a5=10,且a5,a7,a10是某一等比数列{bn}的第1,3,5项,(1)求数列{an}的第20项,(2)求数列{bn}的通项公式.
解:(1)设数列{an}的公差为d,则a5=10,a7=10+2d,a10=10+5d
因为等比数列{bn}的第1、3、5项也成等比,
所以a72=a5a10
即:(10+2d)2=10(10+5d)
解得d=2.5 ,d=0(舍去)…………………………………………………6分
所以:a20=47.5………………………………………………………………8分
(2)由(1)知{an}为正项数列,所以q2=b3/b1=a7/a5=![]() ………………….10分
………………….10分
bn=b1qn-1=±10(3/2)(n-1)/2………………………………………………………………… 12分
(文科)解:由题意,得
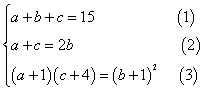
由(1)(2)两式,解得![]()
将![]() 代入(3),整理得
代入(3),整理得

17、经过长期观测得到:在交通繁忙的时段内,某公路段汽车的车流量![]() (千辆/小时)与汽车的平均速度
(千辆/小时)与汽车的平均速度![]() (千米/小时)之间的函数关系为:
(千米/小时)之间的函数关系为:![]() .
.
(1)在该时段内,当汽车的平均速度![]() 为多少时,车流量最大?最大车流量为多少?(保留分数形式)
为多少时,车流量最大?最大车流量为多少?(保留分数形式)
(2)若要求在该时段内车流量超过10千辆/小时,则汽车的平均速度应在什么范围内?(本小题满分10分)
解:(Ⅰ)依题意,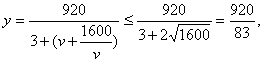 ……………3
……………3
 …….6 分
…….6 分
(Ⅱ)由条件得![]()
整理得v2-89v+1600<0,………………………………………………8分
即(v-25)(v-64)<0,
解得25<v<64. ……………………………………………………….;10
答:当v=40千米/小时,车流量最大,最大车流量约为11.1千辆/小时.如果要求在该时段内车流量超过10千辆/小时,则汽车的平均速度应大于25千米/小时且小于64千米/小时.………………………12 分
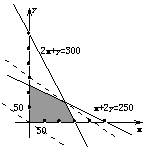
18、分析:将已知数据列成下表:
|
| 甲种棉纱 (1吨) | 乙种棉纱 (1吨) | 资源限额 (吨) |
| 一级子棉(吨) | 2 | 1 | 300 |
| 二级子棉(吨) | 1 | 2 | 250 |
| 利 润(元) | 600 | 900 |
解:设生产甲、乙两种棉纱分别为x吨、y吨,利润总额为z元,
那么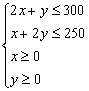
z=600x+900y.
作出以上不等式组所表示的平面区域(如图),即可行域.
作直线l:600x+900y=0,即直线l:2x+3y=0,把直线l向右上方平移至l1的位置时,直线经过可行域上的点M,且与原点距离最大,此时z=600x+900y取最大值.解方程组
![]() 得M的坐标为x=
得M的坐标为x=![]() ≈117,y=
≈117,y=![]() ≈67.
≈67.
答:应生产甲种棉纱117吨,乙种棉纱67吨,能使利润总额达到最大.
19、已知![]() 成等差数列.又数列
成等差数列.又数列![]() 此数列的前n项的和Sn(
此数列的前n项的和Sn(![]() )对所有大于1的正整数n都有
)对所有大于1的正整数n都有![]()
(1)求数列![]() 的第n+1项;
的第n+1项;
(2)若![]() 的等比中项,且Tn为{bn}的前n项和,求Tn.
的等比中项,且Tn为{bn}的前n项和,求Tn.
解:(1)![]() 成等差数列,∴
成等差数列,∴![]()
∴![]() …………2分
…………2分
∵![]() ,
,
∴![]()
∴{![]() }是以
}是以![]() 为公差的等差数列.……………………4分
为公差的等差数列.……………………4分
∵![]() ,
,
∴![]()
∴![]() …………6分
…………6分
(2)∵数列![]() 的等比中项,∴
的等比中项,∴![]() …………8分
…………8分
∴![]()
∴![]() ……10
……10
20、A(Ⅰ)证明:由条件当-1≤x≤1时,│f(x)│≤1,取x=0得
│c│=│f(0)│≤1,
即│c│≤1. 3分
(Ⅱ)证法一:
当a>0时,g(x)=ax+b在[-1,1]上是增函数,
∴g(-1)≤g(x)≤g(1),
∵│f(x)│≤1(-1≤x≤1),│c│≤1,
∴g(1)=a+b=f(1)-c≤│f(1)│+│c│≤2,
g(-1)=-a+b=-f(-1)+c≥-(│f(-1)│+│c│≥-2,
由此得│g(x)│≤2; 7分
当a<0时,g(x)=ax+b在[-1,1]上是减函数,
∴g(-1)≥g(x)≥g(1),
∵│f(x)│≤1(-1≤x≤1),│c│≤1,
∴g(-1)=-a+b=-f(-1)+c≤│f(-1)│+│c│≤2,
g(1)=a+b=f(1)-c≥-(│f(1)│+│c│)≥-2,
由此得│g(x)│≤2; 9分
当a=0时,g(x)=b,f(x)=bx+c.
∵-1≤x≤1,
∴│g(x)│=│f(1)-c│≤│f(1)│+│c│≤2.
综上得│g(x)│≤2. 10分
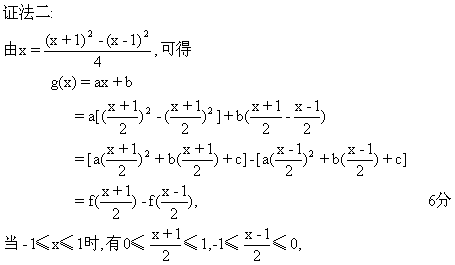
根据含绝对值的不等式的性质,得
![]()
即 │g(x)│≤2. 8分
(Ⅲ)因为a>0,g(x)在[-1,1]上是增函数,当x=1时取得最大值2,
即g(1)=a+b=f(1)-f(0)=2.①
∵-1≤f(0)=f(1)-2≤1-2=-1,
∴c=f(0)=-1. 12分
因为当-1≤x≤1时,f(x)≥-1,即f(x)≥f(0),
根据二次函数的性质,直线x=0为f(x)的图象的对称轴,由此得
![]()
由① 得a=2.
所以 f(x)=2x2-1. 14分
B、


 产品
产品