高中学生学科素质训练
高二数学同步测试(8)—双曲线及几何性质
共150分,考试用时120分钟
一、选择题(本题每小题5分,共60分)
1.设c、e分别是双曲线的半焦距和离心率,则双曲线![]() (a>0, b>0)的一个顶点到它的一条渐近线的距离是
( )
(a>0, b>0)的一个顶点到它的一条渐近线的距离是
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.双曲线![]() 的两焦点为F1,F2,P在双曲线上,且满足PF1+PF2=
的两焦点为F1,F2,P在双曲线上,且满足PF1+PF2=![]() 则△PF
则△PF
A.![]() B.
B.
3.二次曲线![]() ,
,![]() 时,该曲线的离心率e的取值范围是 ( )
时,该曲线的离心率e的取值范围是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.已知椭圆![]() 与双曲线
与双曲线![]() 有相同的焦点
有相同的焦点![]() 和
和
![]() .若
.若![]() 是
是![]() 的等比中项,
的等比中项,![]() 是
是![]() 与
与![]() 的等差中项,则椭圆的离心率是( )
的等差中项,则椭圆的离心率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.已知双曲线![]() 的左,右焦点分别为
的左,右焦点分别为![]() ,点P在双曲线的右支上,且
,点P在双曲线的右支上,且![]() ,则双曲线的离心率e的最大值为 ( )
,则双曲线的离心率e的最大值为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.如果双曲线![]() 上一点P到右焦点的距离等于
上一点P到右焦点的距离等于![]() ,那么点P到右准线的距离
,那么点P到右准线的距离
是 ( )
A.![]() B.13
C.5 D.
B.13
C.5 D.![]()
7.若双曲线![]() 的焦点到它对应的准线的距离2,k= ( )
的焦点到它对应的准线的距离2,k= ( )
A. 6 B. 8 C. 1 D. 4
8.设P是双曲线![]() 上一点,双曲线的一条渐近线方程为
上一点,双曲线的一条渐近线方程为![]() 、F2分
、F2分
别是双曲线的左、右焦点,若![]() ,则
,则![]() ( )
( )
A.1或5 B. 6 C. 7 D. 9
9.若椭圆![]() 与双曲
与双曲![]() 有相同的焦点F1,F2,P是两条曲线的一个交点,则PF1·PF2的值为 ( )
有相同的焦点F1,F2,P是两条曲线的一个交点,则PF1·PF2的值为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.双曲线方程为![]() ,那么k的取值范围是 ( )
,那么k的取值范围是 ( )
A.k>5 B.2<k<5 C.-2<k<2 D.-2<k<2或k>5
11.双曲线的渐近线方程是y=±2x,那么双曲线方程是 ( )
A.x2-4y2=1 B.x2-4y2=1 C.4x2-y2=-1 D.4x2-y2=1
12.过原点作直线![]() 与双曲线
与双曲线![]() 相交,则直线l的斜率k的取值范围是 ( )
相交,则直线l的斜率k的取值范围是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
二、填空题(本题每小题4分,共16分)
13.设双曲线![]() 的一条准线与两条渐近线交于A、B两点,相应的焦点为F,若以AB为直径的圆恰好过F点,则离心率为
的一条准线与两条渐近线交于A、B两点,相应的焦点为F,若以AB为直径的圆恰好过F点,则离心率为
14.双曲线![]() 的离心率为
的离心率为![]() ,则a:b=
,则a:b=
15.双曲线![]() 的两个焦点为F1,F2,点P在双曲线上,若
的两个焦点为F1,F2,点P在双曲线上,若![]() ,则P到x轴的距离为
,则P到x轴的距离为
16.设P是双曲线![]() 上一点,双曲线的一条渐近线方程为
上一点,双曲线的一条渐近线方程为![]() ,F1、F2分别是双曲线的左、右焦点.若PF1=3,则点P到双曲线右准线的距离是
.
,F1、F2分别是双曲线的左、右焦点.若PF1=3,则点P到双曲线右准线的距离是
.
三、解答题(本大题共6小题,共74分。解答应写出文字说明,证明过程或演算步骤)
17.(本题12分) 给定双曲线![]() 。过A(2,1)的直线与双曲线交于两点
。过A(2,1)的直线与双曲线交于两点![]() 及
及![]() ,求线段
,求线段![]()
![]() 的中点P的轨迹方程.
的中点P的轨迹方程.
18.(本题12分). 若双曲线方程为![]() ,AB为不平行于对称轴且不过原点的弦,M为AB中点,设AB、OM的斜率分别为
,AB为不平行于对称轴且不过原点的弦,M为AB中点,设AB、OM的斜率分别为![]() ,则
,则![]() .
.
19.(本题12分)已知双曲线![]() 的离心率
的离心率![]() ,过
,过![]() 的直线到原点的距离是
的直线到原点的距离是![]()
(1)求双曲线的方程;
(2)已知直线![]() 交双曲线于不同的点C,D且C,D都在以B为圆心的圆上,求k的值.
交双曲线于不同的点C,D且C,D都在以B为圆心的圆上,求k的值.
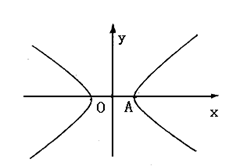
20.(本题12分) 某工程要将直线公路l一侧的土石,通过公路上的两个道口A和B,沿着道路AP、BP运往公路另一侧的P处,PA=100m,PB=150m,∠APB=60°,试说明怎样运土石最省工?
21.(本题12分)已知梯形ABCD中,AB=2CD,点E满足![]() ,双曲线过C、D、E三点,且以A、B为焦点,当
,双曲线过C、D、E三点,且以A、B为焦点,当![]() 时,求双曲线离心率e的取值范围.
时,求双曲线离心率e的取值范围.
22.(本题14分)直线![]() 的右支交于不同的两点A、B.
的右支交于不同的两点A、B.
 (1)求实数k的取值范围;
(1)求实数k的取值范围;
(2)是否存在实数k,使得以线段AB为直径的圆经过双曲线C的右焦点F?若存在,求出k的值;若不存在,说明理由.
参考答案(8)
一.选择题 (本大题共12小题, 每小题5分, 共60分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | D | B | C | A | B | A | A | C | A | D | D | B |
二.填空题(本大题有4小题, 每小题4分, 共16分)
13. ![]() 14. 4或
14. 4或![]() 15.
15. ![]() 16.
16. ![]()
三解答题(本大题共6题,共74分)
17.(本题12分)。分析:设![]() ,
,![]() 代入方程得
代入方程得![]() ,
,![]() .
.
两式相减得
![]() 。
。
又设中点P(x,y),将![]() ,
,![]() 代入,当
代入,当![]() 时得
时得
![]() 。
。
又![]() , 代入得
, 代入得![]() 。
。
当弦![]() 斜率不存在时,其中点P(2,0)的坐标也满足上述方程。因此所求轨迹方程
斜率不存在时,其中点P(2,0)的坐标也满足上述方程。因此所求轨迹方程
是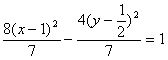 。
。
18.(本题12分)解:设A(![]() ),B(
),B(![]() )则M(
)则M(![]() )
)
又![]() A、B分别在
A、B分别在![]() 上,则有
上,则有
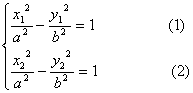
由![]() 得
得![]() ,
,
即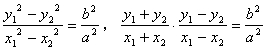 ,
,
![]()
![]()
19.(本题12分)∵(1)![]() 原点到直线AB:
原点到直线AB:![]() 的距离
的距离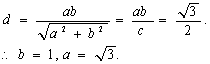 .
.
故所求双曲线方程为 ![]()
(2)把![]() 中消去y,整理得
中消去y,整理得 ![]() .
.
设![]() 的中点是
的中点是![]() ,则
,则
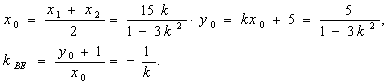
![]()
即![]()
故所求k=±![]() .
为了求出
.
为了求出![]() 的值, 需要通过消元, 想法设法建构
的值, 需要通过消元, 想法设法建构![]() 的方程.
的方程.
20. (本题12分)以直线l为x轴,线段AB的中点为原点对立直角坐标系,则在l一侧必存在经A到P和经B到P路程相等的点,设这样的点为M,则
![]() MA+AP=MB+BP, 即 MA-MB=BP-AP=50,
MA+AP=MB+BP, 即 MA-MB=BP-AP=50,
![]()
![]() , ∴M在双曲线
的右支上.
, ∴M在双曲线
的右支上.
故曲线右侧的土石层经道口B沿BP运往P处,曲线左侧的土石层经道口A沿AP运往
P处,按这种方法运土石最省工.
21.(本题12分)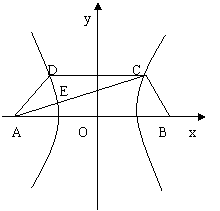 显然,我们只要找到e与
显然,我们只要找到e与![]() 的关系,然后利用解不等式或求函数的值域即可求出e的范围。
的关系,然后利用解不等式或求函数的值域即可求出e的范围。
如图建立坐标系,这时CD⊥y轴,
因为双曲线经过点C、D,且以A、B为焦点,
由双曲线的对称性知C、D关于y轴对称。
依题意,记A(-C,0),C(![]() h),E(x0,y0),其中
h),E(x0,y0),其中
c=![]() 为双曲线的半焦距,h是梯形的高。
为双曲线的半焦距,h是梯形的高。
由![]() ,即(x0+c,y0)=
,即(x0+c,y0)= ![]() (
(![]() -x0,h-y0)
-x0,h-y0)
得:x0=![]() .设双曲线的方程为
.设双曲线的方程为![]() ,则离心率e=
,则离心率e=![]() 。由点C、E
。由点C、E
在双曲线上,将点C、E的坐标和e=![]() 代入双曲线的方程得
代入双曲线的方程得
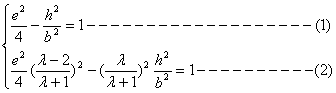
将(1)式代入(2)式,整理得![]() (4-4
(4-4![]() )=1+2
)=1+2![]() ,故
,故![]() =1
=1![]() .
.
依题设![]() 得
得![]() ,解得
,解得![]() .
.
所以双曲线的离心率的取值范围是![]() .
.
 22.(本题14分)(1)将直线l的方程
22.(本题14分)(1)将直线l的方程![]() 代入双曲线C的方程
代入双曲线C的方程![]() 后,整
后,整
理得![]() ……①
……①
依题意,直线l与双曲线C的右支交于不同两点,
故
(2)设A、B两点的坐标分别为![]() 、
、![]() ,则由①式得
,则由①式得
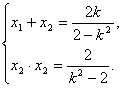 ……②
……②
假设存在实数k,使得以线段AB为直径的圆经过双曲线C的右焦点F(c,0).
则由FA⊥FB得:![]()
整理得![]() ……③把②式及
……③把②式及![]() 代入③式
代入③式
化简得
