钱库第二高级中学数学期末考试试卷10
第Ⅰ卷（选择题共60分）
一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有
一项是符合题目要求的。
1．不等式
的解集是 （ ）
A．
B．
C．
D．
2．过点M（－2，4）作圆C：
的切线l，直线
与l平行，则l1与l之间的距离是 （ ）
A．
B．
C．
D．
3．已知下列各不等式：（1）
（2）
、
（3）
、其中正确的是 （ ）
A．（2） B．（2）（3） C．（1）（3） D．（1）（2）（3）
4．若双曲线的一个顶点到两条准线的距离和等于4，一个焦点到两条渐近线的距离和等于8，
则双曲线的离心率的值是 （ ）
A．
B．
C．
D．
5．设坐标原点为O，抛物线
与过焦点的直线交于A、B两点，则
的值是
（ ）
A．
B．
C．3 D．－3
6．已知
则一定有 （ ）
A．
B．
C．
D．
7．能使
的实数
的取值范围是 （ ）
A．（0，1） B．
C．
D．
8．已知点
是圆
内一点，直线m是以P为中点的弦所在的
直线，若直线n的方程为
则 （ ）
A．m//n且n与圆O相离 B．m//n且n与圆O相交
C．m与n重合，且n与圆O相离 D．m⊥n且n与圆O相离
9．
是定义在
上的奇函数，若
时的图象如图所示，那么不
|
的解集是 （ ）
A．
B．
C．
D．
10．过椭圆
的一个焦点F作弦AB，若AF=d1，BF=d2，则
的数值为 （ ）
A．
B．
C．
D．与a、b斜率有关
11．已知F1、F2是两个定点，点P是以F1和F2为公共焦点的椭圆和双曲线的一个交点，并
且PF1⊥PF2，e1和e2分别是椭圆和双曲线的离心率，则有 （ ）
A．
B．
C．
D．
12．某人获悉一个岛上有三处藏有宝物，由于年代久远，有的数据缺失，记载如下：岛上有
一棵椰子树，由椰子树动向东走3米为藏宝处A，继续向东走b米，到达B处，然后向
东偏北60°走a米为藏宝处C（其中a、b为缺失数据）由B向南走
BC为藏宝处E，
三个藏宝处在以B为焦点，椰子树的南北方向所在的直线为相应准线的双曲线上，寻宝
关键推出a、b的值，a、b的准确值分别为 （ ）
A．28 4 B．14 4 C．28 8 D．14 8
二、填空题：本大题共4小题，每小题4分，共16分，把答案填在题中横线上
13．已知P是抛物线
上的动点，定点A（0，－1）若M分
所成的比为2，
则动点M的轨迹方程是 .
14．a、b∈R则下列四个条件中是a+b＞1成立的充分不必要条件是 .
（1）
（2）
（3）
（4）
15．已知
的最小值为
16．下面等号右侧两个分数的分母处，各填上一个自然数，并且使这两个自然数的和最小
三、解答题：本大题共6小题，共74分，解答应写出文字说明、证明过程或演算步骤.
17．（本小题满分12分）设
，解关于x的不等式
18．（本小题满分12分）已知A（2，0）、B（0，6），O为坐标原点，
（1）若C点在线段OB上；且
，求
的面积；
（2）若原点O关于直线AB的对称点为D，延长BD到P，且PD=2BD，已知直线
经过点P，求直线
的倾斜角.
19．（本小题满分12分）过双曲线
的右焦点F作直线
，使垂直于斜率为正值的C的渐近线；垂足为P，设与C的左右支分别交于A、B
两点.
（1）求证：P点在C的右准线上；
（2）求C的离心率e的取值范围.
20．（本小题满分12分）某商场预计全年分批购入每台价值为2000元的电视机共3600台，
每批都购入x台（x是正整数），且每批均需付运费400元，储存购入的电视机全年所付
保管费与每批购入电视机的总价值（不含运费）成正比。若每批购入400台，则全年需
用去运费和保管费用43600元，现在全年只有24000元资金可以用于支付这笔费用，请
问能否恰当安排每批进货的数量，使资金够用？写出你的结论，并说明理由.
21．（本小题满分12分）二次函数
，已知
且
；（1）求证：
（2）求证：
；（3）若
的解集是
解析式.
22．（本小题满分14分）已知抛物线
的弦AB与直线y=1有公共点，且弦AB的中点
N到y轴的距离为1，求弦AB长度的最大值，并求此直线AB所在的直线的方程.
|
2003—2004学年度第一学期期末二省一市四校联考
高二数学试卷参考答案
一、选择题1—6：BBCCBA 7—12：BABBDA
二、填空题13．
14．（2） 15．－16 16．4，12
三、解答题：
17．解：原不等式可化为：
等价于
……（1） （4分）
当
时由（1）得
（6分）
当
时由（1）得
（8分）
当
时
（10分）
综上所述：
（12分）
18．解（1）要求△ABC的面积，关键是求C点的坐标，可利用夹角公式先求直线AC的斜
率，在写出直线AC的方程，从而可求出C点坐标.
令
（5分）
（2）要求直线l的倾斜角，需要参数a的值。由直线l过点P，所以需求出P点的坐标，
由P是BD的定比分点，所以还需由对称性求出D点的坐标.
设D点坐标为
，
（8分）
由PD=2BD得
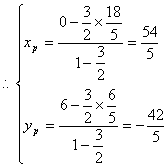
将点
代入L的方程中，得
（11分）
故直线的倾斜角为
（12分）
19．（1）证明：设C的右焦点F（c，0），斜率为正值的C的渐近线方程为
则l的方程为
（3分）
由
故点P在C的右准线上. （6分）
（2）由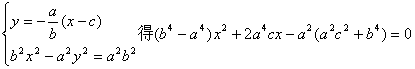
，
∴由韦达定理：
（8分）
由于A、B是左、右支上的点，
（10分）
所以
（12分）
20．解：设每批购入电视机x台时，全年费用为y元，保管费与每批电视机总价值的比例系
数为k，据题意，有
，由已知x=400时，y=43600，代入上式，
解得
，当且仅当
时，等号成立，即x=120台时，全年共需资金24000元.
答：每批购进电视机120台时，全年的资金24000元够用
21．（1）证明：
，
是方程
的两根
根据根与系数的关系有：
由已知
（4分）
（2）证明：
，
（7分）
（3）解：
的解集是
的解集是
（12分）
22．解：设
、
，中点
当AB直线的倾斜角90°时，AB直线方程是
（2分）
当AB直线的倾斜角不为90°时，
相减得
所以
（4分）
设AB直线方程为：
，由于弦AB与直线y=1有公共点，故当y=1时
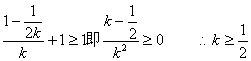（6分）
所以
，故
（8分）
故当
（14分）