2004－2005学年度下学期
高中学生学科素质训练
高二数学同步测试（3）— 平面和平面的位置关系
YCY
本试卷分第Ⅰ卷和第Ⅱ卷两部分.共150分.
第Ⅰ卷（选择题，共50分）
一、选择题：本大题共12个小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．
1．下列命题中正确的是 （ ）
A．垂直于同一平面的两平面平行
B．垂直于同一直线的两平面平行
C．与一直线成等角的两平面平行
D．RtÐABC在平面a的射影仍是一个直角，则ÐABC所在平面与平面a平行
2．ABCD是一个四面体，在四个面中最多有几个是直角三角形 （ ）
A．1 B．2 C．3 D．4
3．已知
、
是不重合的直线，a、b是不重合的平面，有下列命题：
①若
a、∥b,则∥；
②若∥a、∥b,则a∥b；
③若a∩b＝，∥，则∥a，∥b；④若⊥a，⊥b，则a∥b．
其中真命题的个数是 （ ）
A．0 B．1 C．2 D．3
4．已知二面角α－AB－β的平面角为θ，α内一点C到β的距离为3，到棱AB的距离为4，
则tanθ等于 （ ）
A．
B．
C．
D．
5．下列命题：① 若直线a//平面
，平面⊥平面β，则⊥β; ② 平面⊥平面β，平
面β⊥平面γ，则⊥γ；③ 直线a⊥平面，平面⊥平面β，则a//β； ④ 平面//
平面β，直线a平面，则a//β．其中正确命题的个数是
（ ）
A．1 B．2 C．3 D．4
|
（它不在棱AB上），点D是C在平面β内的射影，点E
是AB上满足∠CEB为锐角的任意一点，那么（ ）
A．∠CEB>∠DEB B．∠CEB<∠DEB
C．∠CEB=∠DEB D．无法确定
7．如果直线l、m与平面α、β、γ满足：
，
，
，那么必有（ ）
A．
B．
C．
D．
|
∠DCE＝β，∠BDC＝θ，则 （ ）
A．sinα＝sinβsinθ B．sinβ＝sinαcosθ
C．cosα＝cosβcosθ D．cosβ＝cosαcosθ
9．若有平面
与
，且
，则下列命
题中的假命题为 （ ）
A．过点
且垂直于的直线平行于 B．过点且垂直于
的平面垂直于
C．过点且垂直于的直线在内 D．过点且垂直于的直线在内
10．空间三条射线PA，PB，PC满足∠APC=∠APB=60°，∠BPC=90°，则二面角B-PA-C 的度数 （ ）
A．等于90°
B．是小于120°的钝角
C．是大于等于120°小于等于135°的钝角
D．是大于135°小于等于150°的钝角
第Ⅱ卷（非选择题，共100分）
二、填空题：本大题满分24分，每小题6分，各题只要求直接写出结果.
|
则（1）面EFG与面ABCD所成的角为 ；
（2）面EFG与面ADD1A1所成的角为 ．
12．斜线PA、PB于平面α分别成40°和60°，则∠APB的取
值范围为
13．在直角△ABC中，两直角边AC＝b，BC＝a，CD⊥AB于D，
|
cos∠ACB＝ ．
14．如图，两个矩形ABCD和ABEF中，AD＝AF＝1，
DC＝EF＝2
，则AB与CF所成角θ的大小范
围是 ．
三、解答题：本大题满分76分.
15．（本小题满分12分）
求证：
．
16．（本小题满分12分）正方体ABCD-A′B′C′D′棱长为1．
|
（2）求点B′到面A′BD的距离．（14分）
17．（本小题满分12分）如图，平面α∥平面β，点A、C∈α，B、D∈β，点E、F分
|
，求证：EF∥β.
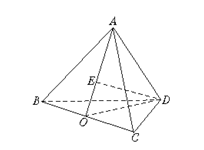
18．（本小题满分12分）如图，四面体ABCD中，△ABC与△DBC都是边长为4的正三角形.（1）求证：BC⊥AD；
（2）若点D到平面ABC的距离不小于3，求二面角A—BC—D的平面角的取值范围；
|
19．（本小题满分14分）在长方体
中，
，底边
上有且
|
使得平面
平面
.
（1）求异面直线
与
的距离；
（2）求二面角
的大小.
|
（1）证明AD⊥D1F;
（2）求AE与D1F所成的角;
（3）证明面AED⊥面A1FD1;
（4）
．
参考答案（三）
一、选择题（本大题共10小题，每小题5分，共50分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | B | D | B | C | A | A | A | A | D | B |
二、填空题（本大题共4小题，每小题6分，共24分）
11．
12．
13．
14．
三、解答题（本大题共6题，共76分）
15．(12分) 证明：过b上一点作平面
与α相交于b′
16．(12分) （1）证明：∵A’D∥B’C，DB∥D’B’
又∵A’D∩DB＝D，B’C∩D’B’＝B’ ∴面A’BD∥面B’CD’
（2）解法一：易知B′到平面A′BD的距离d等于A到平面A′BD的距离，
且△A′BD为等边三角形
由
可知
解得
∴
解法二：易知B′到面A′BD的距离d等于A到面A′BD的距离
沿A′BD截下三棱锥A-A′BD，易知是一个正三棱锥
过A作AF⊥A′BD，则AF即为A到平面A′BD的距离
如右图，DE为A′B的中线，且F为△A′BD的中心
，
即A到平面A′BD的距离为
.
17．(12分) 证明：过A作AH∥CD交β于H，连结HD、HB、BD、AC.
∵α∥β ∴AH=CD∴四边形AHDC是平行四边形，
∴AC∥HD, 过F作FG∥HD交AH于G，连结GE
∴AC∥GF∥HD ∴GF∥β，∴
,∵
∴
,∴EG∥BH ∴EG∥β
∵EG∩GF=G ∴平面EGF∥β ∵EF
平面EGF
∴EF∥β
18．(12分) （1）证明：取BC中点O，连结AO、DO
∵△ABC与△DBC都是边长为4的正三角形
∴AO⊥BC，DO⊥BC
∴BC⊥平面AOD ∵AD平面AOD ∴BC⊥AD
（2）解：由（1）知∠AOD为二面角A—BC—D的平面角，
设∠AOD=θ,作DE⊥AO于E，由（1）知平面AOD⊥平面ABC，
且平面AOD∩平面ABC=AO
∴DE⊥平面ABC，DE为D到平面ABC的距离，
又DO=
BD=2
∴DE=DOsinθ=2sinθ
∵DE≥3
∴sinθ≥ ∵θ∈(0,π)∴θ∈［
］
（3）∵S△ABC=
×42=4 ∵DE=DOsinθ=2sinθ,θ∈［］
∴DE≤2,DE的最大值为2 ∵VD—ABC=
×S△ABC×DE=×4×DE
∴当DE最大时，有VD—ABC=×4×2=8∴四面体ABCD的体积的最大值为8.
19．（14分）证明:(1)过
作
于
∵平面
平面且平面
平面
∴
平面∴
又∵
∴
平面
∴
又∵满足条件的只有一个
∴以
为直径的圆必与相切，
切点为，为的中点
∴
∴
∵平面，∴
又∵
，所以
为异面直线
与的公垂线段
的长度为所求距离 
（2）取中点
，连结
，则
平面
, 过作
于
，连结
，则
,∴
为二面角的平面角
又∵
,
，在
中
∴
20．(14分) 解法一:（1）∵AC1是正方体，∴AD⊥面DC1. 又D1F
面DC1， ∴AD⊥D1F.
（2）取AB中点G,连结A1G，FG.因为F是CD的中点,所以GF、AD平行且相等,又A1D1、AD平行且相等,所以GF、A1D1平行且相等,故GFD1A1是平行四边形,A1G∥D1F.
设A1G与AE相交于点H,则∠AHA1是AE与D1F所成的角，
因为E是BB1的中点,所以Rt△A1AG≌Rt△ABE，
∠GA1A=∠GAH，从而∠AHA1=90°,即直线AE与D1F所成角为直角.
（3）由(Ⅰ)知AD⊥D1F,由(Ⅱ)知AE⊥D1F,又AD∩AE=A,所以D1F⊥面AED.又因为D1F面A1FD1，
所以面AED⊥面A1FD1.
（4）连结GE，GD1. ∵FG∥A1D1,∴FG∥面A1ED1，
∵AA1=2,面积S△A1GE=S□ABB1A1－2S△A1AG－S△GBE=
又
解法二：利用用向量求解
解析：设正方体的棱长为2，以D为原点，DA为x轴，DC为y轴，DD1为z轴建立空间直角坐标系，
则D（0，0，0），A（2，0，0），F（0，1，0），E（2，2，1），A1（2，0，2），D1（0，0，2），
（1） ∵ 
,
，得
，∴ AD⊥D1F;
（2）又
，得
∴ AE与D1F所成的角为90°
（3） 由题意：
，
设平面AED的法向量为
，设平面A1FD1的法向量为
，
由
由
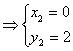
得
∴ 面AED⊥面A1FD1.
（4）∵AA1=2，
，
平面A1FD1的法向量为
， ∴E到平面A1FD1的距离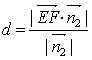
，
．