东里中学第一学期期末考试高二数学试卷（文科）-高中二年级数学试题练习、期中期末试卷、测验题、复习资料-高中数学试卷-试卷下载

东里中学2005-2006学年度第一学期期末考试

高二数学试卷（文科）

号题	一	二	三	分总
号题	一	二		分总
分得

一、　 选择题（本大题共10小题；每小题5分，共50分。在每小题给出的四个选项中，只有一项是符合要求的，请把正确答案的代号填在下面的答案表中）

号题

案答

1、抛物线的准线方程是( 　b　 ).

A. 　　　 B. 　　　　C. 　　　　　D.

2、“a≠1或b≠2”是“a＋b≠3”的（　 d　）

A、充分不必要条件　　 B、必要不充分条件　

C、充要条件　　 D、既不充分也不必要

4、已知，点P在A、B所在的平面内运动且保持，则的最大值和最小值分别是　　(　c )

A．、3　　B．10、2　　C．5、1　　　 D．6、4

1．椭圆的焦点在轴上，长轴长是短轴长的两倍，则的值为（　 a　）

　 A．　　　　　　　　　 B．　　　　C． 2　　　　　　　　　　D．4

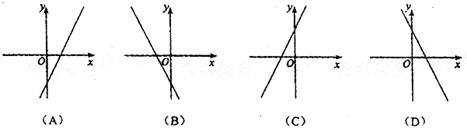
1.若函数f(x)=x²+bx+c的图象的顶点在第四象限，则函数f＇(x)的图象是（ a　）

3．已知命题甲：，命题乙：点是可导函数的极值点，则甲是乙的（b　）

A．充分而不必要条件 B．必要而不充分条件 C．充要条件 D．既不充分而不必要条件

7.若双曲线的两条渐进线的夹角为，则该双曲线的离心率为(　d )

A.2　　B.　　C.2或　　D.2或

6．若物体的运动方程是s(t)=tsint ，则物体在t=2时的瞬时速度为（ c ）

A. cos2+2sin2 　　　 B.2sin2-cos2 　　 C. sin2+2cos2　　　 D.2cos2-sin2

5.曲线y=x³+x-2在点P₀处的切线平行于直线y=4x-1,则P₀的坐标是

A.(0,1)　　　　 B.(1,0)　　　　 C.(-1,0)　　　　 D.(1,4)

18. 函数在区间上单调递增，那么实数a的取值范围是（ a ）

A．　 B．　C．　　D．

8．与圆x²+y²-4y=0外切, 又与x轴相切的圆的圆心轨迹方程是 (　 d　　).　

　　A. y²=8x　　 B. y²=8x (x>0) 和 y=0　　 C. x²=8y (y>0) 　D. x²=8y (y>0) 和 x=0 (y<0)

二、填空题（本大题共4小题；每小题5分，共20分。把答案填在题中横线上）

11．命题的否命题是　　　　　　　　　　.

12．已知p是r的充分不必要条件，s是r的必要条件，q是s的必要条件，那么p是q成立的　　　　条件。（填“充分不必要”“必要不充分”、“充要”或“既不充分也不必要” ）

14、充分不必要

13．若方程所表示的曲线为C，给出下列四个命题：

①若C为椭圆，则1<t<4;　　　②若C为双曲线，则t>4或t<1；

　③曲线C不可能是圆；　　　　④若C表是椭圆，且长轴在x轴上，则.

　其中真命题的序号为　　　　　　　　（把所有正确命题的序号都填在横线上）

（2）

14．函数y=的单调增区间是　　　　　　　，减区间是　　　　　.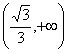

三、解答题:本大题共5小题；共50分。解答应写出文字说明、证明过程或演算步骤。

13.写出命题“若”的逆命题、否命题、逆否命题，并判断它们的真假.

13. 解：逆命题：若

　　　　否命题：若

逆否命题：若

1已知f(x)=x³+ax²+bx，在x=1处有极值－2，求a、b的值.

解：f′(x)=(x³+ax²+bx)′=3x²+2ax+b

∵f(x)在x=1处有极值－2　∴f′(1)=0，且f(1)=－2

∴

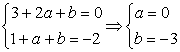
13.求与双曲线有共同的渐近线，并且经过点的双曲线方程．

13. 解:由题意可设所求双曲线方程为：　………4分

双曲线经过点　　　……8分

所求双曲线方程为：　………………………………10分

17．设f(x)=x³-x²-2x+5

（1）求函数f(x)的单调递增，递减区间：

（2）当x∈[-1，2]时，f(x)<m恒成立，求实数m的取值范围。

17.解:(1)令f^/(x)=3x²-x-2>0,得x<-或x>1.

∴函数的单调增区间为(-∞,- )、(1,+∞),单调减区间为(-,1)

(2)原命题等价于f^/(x)在[-1,2]的最大值小于m.由f^/(x)=0,得x= -或1,又f(-1)=,f(-)=5,f(1)=,f(2)=7

∴m>[f(x)]_max=7.

14．-1的直线与抛物线交于两点A，B，如果（O为原点）求P的值及抛物线的焦点坐标。

14．解:直线方程为y=-x+4,联立方程,消去y得,.

设A(),B(),得

所以:,p>0.

由已知可得+=0,从而16-8p=0,得p=2.

所以抛物线方程为y²=4x,焦点坐标为F(1,0).

22.用总长14.8m的钢条制做一个长方体容器的框架,如果所制做容器的底面的一边比另一边长0.5m,那么高为多少时容器的容积的最大?并求出他的最大容积.

22.解:设容器底面积短边长为xm,则另一边长为(x+0.5)m,高为=3.2-2x.由3.2-2x>0和x>0得0<x<1.6,设容器的容积为vm³,则有V=x(x+0.5)(3.2-2x)　(0<x<1.6)即:V=-2x³+2.2x²+1.6x.∴V^/=-6x²+4.4x+1.6.令V^/=0得-6x²+4.4x+1.6=0 即x₁=1,x₂=-(舍去).∴在(0,1.6)内只有x=1处使V^/=0.由题意,若x过小(接近0)或过大(接近1.6)时,V很小(接近0),因此,当x=1时y取得最大值.　　　　 y_大=-2+2.2+1.6=1.8,这时高为3.2-2×1＝1.2