蚌埠市2005—2006学年度第一学期期终教学质量监测
高二数学
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共150分，考试时
间120分钟。
第Ⅰ卷（选择题，共60分）
一、选择题：本大题共12小题，每小题5分，共60分。在每小题给出的A、B、C、D的四个选项中，只有一个选项是符合题目要求的，请将正确答案的字母代号涂到答题卡上。（不用答题卡的，填在第Ⅱ卷中相应的答题栏内）
1、若x+y=2 ,b<x<a, 则下列不等式正确的是（ ）
（A）2-a < y < 2-b (B) 2-b < y < 2-a
(C ) b+2 > y > a+2 (D) b+2 < y < a+2
2、已知x>0 y>0, x≠y, 则下列四个数中最小的数是（ ）
(A) 
(B)
(C)
(D)
3、直线y=kx+b(b≠0)不经过第二象限，则（ ）
（A）k·b<0 (B) k·b≤0 (C) k·b>0 (D) k·b≥0
4、若P=
(m>0) q=arccost(-1≤t≤1),则下列不等式恒成立的是（ ）
(A) P≥4>q>0 (B) P≥
>q (C) 4>P≥q (D) P≥q>0
5、已知直线l1的倾斜角为
1，则l1关于X轴对称的直线的倾斜角2为（ ）
（A）-1 (B) 
- (C) 0或 1 - (D) 0或 -1
6、如果点（5、b）在两条平行直线6x-8y+1=0和 mx-4y+5=0之间，则b应取的整数值为（ ）
(A) 5 (B) -5 (C) -4 (D) 4
7、椭圆
上的点M到左焦点F1的距离为2,N是MF1的中点,则ON等于( )
(A) 2 (B) 4 (C) 8 (D) 3/2
8、已知实数a∈R，则“a>1”是“曲线y-ax=0与直线y-x=a有两个交点”的（ ）
(A)既不充分也不必要条件 （B）必要而不充分条件
(C)充分而不必要条件 (D)充要条件
9、我们把离心率e=
的椭圆称为“优美椭圆”，设
(a>b>0)是优美
椭圆，F 、A分别是它的左焦点和右焦点，B是它短轴的一个端点，则∠ABF等于（ ）
(A) 60o (B)75o (C) 90o (D) 120o
10、双曲线
的两条渐近线夹角的正切值（ ）
(A) - (B) (C) (D)
11、过抛物线y=ax2
(a>0)的焦点F作一直线交抛物线于P、Q两点，若线段PF和FQ的长分别为p、q，则
的值为（ ）
(A) 4a
(B) 2a
(C)
(D) 
12、已知ab≠0,点M(a,b)是圆x2+y2=r2内一点，直线m是以点M为中心的弦所在的直线，直线
的方程是ax+by=r2，则下列结论正确的是（ ）
(A) m // 
且 与圆相交
(B) m // 且 与圆相离
(C) ⊥m 且 与圆相交
(D) 
⊥m , 且 与圆相离
蚌埠市2005—2006学年度第一学期期终教学质量监测
高二数学
第Ⅱ卷（非选择题，共90分）
| 题号 | 一 | 二 | 三 | 总分 | |||||
| 17 | 18 | 19 | 20 | 21 | 22 | ||||
| 得分 | |||||||||
（不用答题卡的，选择题答题栏。用答题卡的不必填）
一、选择题答题栏：
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 小计 |
| 答案 |
第Ⅱ卷（非选择题 共90分）
二、填空题：本大题共4小题，每小题4分，共16分。请将答案直接填在题中横线上。
13、当x>1时，不等式x+
≥a恒成立，则实数a的取值范围是________.
14、过点（5，-2）且在x轴上的截距是在y轴的截距的2倍的直线方程是________.
15、已知关于x的不等式
的解集为
，则实数a,b的值分别为________.
16、以椭圆
的焦点为焦点，以直线y=±
x为渐进线的双曲线方程为_____ ______________.
|
17、(本题满分12分)
解不等式组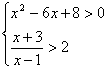
|
18、．（本题满分12分）
直线过点P∈（1，3），求满足下列条件时直线的方程。
(1)与x+y-1=0平行;
(2)与抛物线y2=2x只有一个交点.
|
求圆心在直线
，并且与直线
相切于点
的圆的方程。
|
20、(本题满分12分)
设函数f(x)=x+
x∈[0,+∞
,当a=2时，求函数f(x)的最小值.
|
21、(本题满分12分)
已知椭圆C的中心在原点，焦点在x轴上，一条经过点
且
方向向量为
的直线l通过椭圆C的右焦点F，且交椭圆C
于A、B两点，又
(1)求直线l的方程； （2）求椭圆C的方程.
22、 (本大题满分14分)
如图, 
, 
是双曲线C的两焦点, 直线
是双曲线C的右准线, A1, A2双曲线C的两个顶点, 点P是双曲线C右支上异于A2的一动点, 直线A1P,A2P交双曲线C的右准线分别于M, N两点.
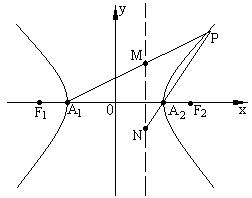(1) 求双曲线C的方程;
(2) 求证: 
是定值.
蚌埠市2005—2006学年度第一学期期终教学质量监测
高二数学试题参考答案及评分标准
一、选择题：本大题共12小题，每小题5分，共60分。
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | A | C | B | A | D | D | B | C | C | D | A | B |
二、填空题：本大题共4小题，每小题4分，共16分。
| 题号 | 13 | 14 | 15 | 16 |
| 答案 | (-∞,3) | X+2y-9=0或2x-5y=0 | 4、2 |
|
三、解答题：本大题共6小题，共74分。
17、（本小题满分12分）
解：由
，得（x-2）（x-4）>0……………………………2分
∴x<2或x>4 …………………………5分
由
,得
…………………………7分
∴1<x<5, ……………10分
∴原不等式的解是(1,2)
(4,5) …………………………12分
18．（本小题满分12分）
解：(1) x+y-4=0…6分
(2)①当l的斜率k=0时，l：y=3………………………8分
②当l的斜率k≠0时（此时斜率必存在）
设l：y-3=k（x -1） 与y2=2x 联立
得 ky2-2y-2（k-3）=0
由△=0，得2k2-6k+1=0
解得 
………………………10分
所以l：
或
………………12分
19、（本小题满分12分）
解：过点Ｐ（３，－２）与切线l 垂直的直线：x-y-5=0
与圆心所在的直线4x+y=0的交点（１，－４）即为所求圆的圆心。……4分
又圆半径r=
…..8分
所以，所求为 (x-1)
+(y+4) ……12分
20、（本小题满分12分）
解：由
………………3分
因为
所以
，………………6分
所以
，………………10分
即
的最小值为
………………………12分
21、（本小题满分12分）
解：（1）直线l过点（3，－
）且方向向量为
……………………………………（4分）
（2）设直线
，
由
……………………………………………………（6分）
将
，
整理得
|
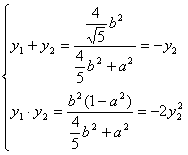（8分）
由①2/②知 
……………………………………（10分）
又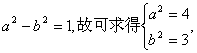
因此所求椭圆方程为：
…（12分）
22、（本小题满分14分）
解: (1)由已知, 
∴
所以求双曲线C的方程为
…………(6分)
(2)设P的坐标为
, M, N的纵坐标分别为
∵
, ∴
…………(8分)
∵
与共线, ∴
同理
…………(10分)
∵
∴
·
＝
…………(12分)
＝
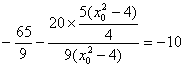…………(14分)