北大附中云南实验学校上学期期末测试高二数学

北大附中云南实验学校2005-2006学年上学期期末测试

高二数学

一.　选择题：本大题共12小题，每小题4分，共48分．在每小题给出的四个选项中，只有一项是符合题目要求的．

1.若,则下列不等式一定成立的是(　　 )

A. 　　　　　B. 　　　 　 C. 　　　　　D.>0

2.到定点的距离与到定直线的距离之比等于log₂3的点的轨迹是(　　　 )
　 A．圆　　　　　　　　　　　　 B．椭圆　　　　　　　　　 C．双曲线　　　　　　　　　　 D．抛物线

3.在直角坐标系中,直线的倾斜角为(　　　 )

A.　　　　　 　 B.　 　　　　　C.  　　　　　 D.

4.如果直线ax＋2y＋2＝0与直线3x－y－2＝0平行，那么实数a＝(　　　)
　　A．－6　　　　　 B．－3　 　　　　　C．　　 　　　　　D．

5.椭圆的焦点坐标为(　　　)

A. 　　　B. 　 C.　 D.

6.抛物线上一点P到焦点F的距离为5,则P点的横坐标为(　　 )

A.　3　　　　　　  B.  4　　　　　  C.　 5　　　　　　  D.　　6

7.从点P发出的光线,经过直线反射,若反射光线恰好经过点,则光线所在的直线方程是(　　　)

A. 　　B. 　 C. 　 D.

8.正方体ABCD—A₁B₁C₁D₁中，p、q、r、分别是AB、AD、B₁C₁的中点。那么正方体的过P、Q、R的截面图形是(　　　)

A.三角形　　　 　 B.四边形　　　　  C.五边形　　　　  D.六边形

9.已知点P(x，y)在不等式组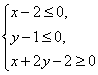表示的平面区域上运动，则z＝x－y的取值范围是(　　)

A．[－2，－1]　　　B．[－2，1]　　　　C．[－1，2]　　　D．[1，2]

10.若点(a，b)是直线x＋2y－1＝0上的一个动点，则ab的最大值是(　　　)
　　　　A．　　　　　　　　　　　 B．　 　　　　　　 C．　　　　　　　　　　　D．

11.已知a、b、c是直线，是平面，给出下列命题：　　　　　　

　 　　 ①若；

　　　 　 ②若；

　　　 　 ③若；

　　　 　 ④若a与b异面，且相交；

　　　 ⑤若a与b异面，则至多有一条直线与a，b都垂直.

　　其中真命题的个数是(　　　)

　　　 　　A．1　　　　　  B．2　　　　　　　　　　　C．3　　　　　　　　D．4

12. 对满足不等式的一切实数a，不等式都成立，则实数x的取值范围是(　　　)
　　　　 A．＜x＜9　　　　　 B．≤x≤9　　　　　 C．x＜或x＞9　　　　　　 D．x≤或x≥9

二.　填空题：本大题共4个小题，每小题4分，共16分.　将正确答案填在题中横线上．

13. 若直线x＋3y－7＝0与直线kx－y－2＝0的方向向量分别为，则当时，实数k的值为　　.

14. 若恒成立，则m的取值范围是　　　　　　　.

15. 双曲线的渐近线为,则双曲线的离心率为　　　　　　　　.

16. 抛物线上任一点到直线的距离的最小值是　　　　　　　　.

三.　解答题：本大题共5个小题，共36分.　解答要写出必要的解题步骤，证明过程，或文字说明.

17.（本小题满分6分）求经过，和直线相切，且圆心在直线上的圆的方程。

18．（本小题满分6分）解关于x的不等式

19．(本小题满分8分) 已知直线过点（2，3），且和两平行直线 、分别相交于、两点，如果，求直线的方程。

20．(本小题满分8分)已知椭圆具有性质：若A是椭圆C的一条与x轴不垂直的弦的中点，那么该弦的斜率等于点A的横、纵坐标的比值与某一常数的积．试对双曲线写出类似的性质，并加以证明．
 

21．(本小题满分8分) 如图，直线l₁和l₂相交于点M，且，点，以A、B为端点的曲线段C上的任意一点到l₂的距离与到点N的距离相等，若△AMN为锐角三角形,，试建立适当的坐标系，求曲线段C的方程。

　　

高二数学期末试题答案

一．选择题：

　 1．C　 2. C　 3. D　4.A  5.　B　 6. B　 7.C　 8. D　 9. C　 10. C　 11.A　12.B

二．填空题：

　 13． 3　　  14. 　　　15.　或　　  16.　

三.解答题:

17．解：因为圆心在直线上，所以可设圆心坐标为，根据题意，

，　　得a=1

所以，圆心为，半径为。从而所求的圆的方程为

18．解：（x－a）（x－a²）＜0，∴x₁＝a，x₂＝a²

当a=a²时，a=0或a=1，x∈，

当a＜a²时，a＞1或a＜0，a＜x＜a²，

当a＞a²时0＜a＜1，a²＜x＜a，

∴当a＜0时a＜x＜a²，当0＜a＜1时，a²＜x＜a，当a＞1时，a＜x＜a²，当a=0或a=1时，x∈

19．解：两直线间的距离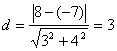　　　　　　　　　 　　　　　　

　　又，故与成角　　　　　　　 　　　　　　　　　　　 

设所求直线的斜率为，故　　　　　　　　　　　

∴或　　　　　　　　  　　　　　　　　　 

∴或　　　　　　　　 　　　　　　　　　

 20．解：双曲线性质：若A是双曲线C：的一条与x轴不垂直的弦的中点，那么该弦的斜率于点A的横、纵坐标的比值与常数的积．　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

证明如下：设A(x₀，y₀)，弦的两端点为C(x₁，y₁)、D(x₂，y₂)，则
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

两式相减得：
　　由于A是线段CD的中点，∴x₁＋x₂＝2x₀，y₁＋y₂＝2y₀
　　∴　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　
　　又CD与x轴不垂直，故其斜率k存在，且，∴结论成立．　　

21．如图，建立坐标系，以l₁为x轴，MN的垂直平分线为y轴，点O为坐标原点.

依题意知：曲线段C是以点N为焦点，以l₂为准线的抛物线的一段，其中A、B分别为C的端点.

设曲线段C的方程为

y²=2px（p＞0），（x_A≤x≤x_B，y＞0）

其中x_A、x_B分别为A、B的横坐标，p＝MN．

所以M（，0），N（，0）

由AM＝，AN＝3得

（x_A＋）²＋2px_A＝17　　　　　　 ①

（x_A）²＋2px_A＝9　　　　　　　 ②

由①②两式联立解得x_A＝，再将其代入①式并由p>0

解得或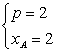

因为△AMN是锐角三角形，所以＞x_A，

故舍去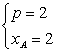

所以p＝4，x_A＝1．

由点B在曲线段C上，得x_B＝BN＝4．

综上得曲线段C的方程为y²＝8x（1≤x≤4，y＞0）．