北京西城区下学期高二数学期末考试

北京西城区02-03年下学期高二数学期末考试

（120分钟，满分100分）

一、选择题（本大题共10个小题，每小题4分.共40分，在每小题给出的四个选项中，只有一项是符合题目要求的，每小题选出答案后，将答案填在题中的括号内）

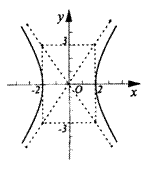1. 右图中双曲线的方程为（　　 ）

（A）=1　　　　　  （B）=1

（C）=1　　　　　  （B）=1

2. 复数i·（1+i）²的值是（　　 ）

（A）2　　　　　 （B）-2　　　　　　　　　　 （C）2i　　　　　　 （D）-2i

3. 若=a-2，则实数a的值是（　　 ）

（A）-2　　　　  （B）-3　　　　　　　　　　 （C）2　　　　　　  （D）3

4. [理]将极坐标方程ρcos（θ+）=1转化为直角坐标方程是（　　 ）

（A）x-y-2=0　　　　　　　  （B）x+y-2=0

（C）-y-2=0　　　　　　　　 （D）x+y-2=0

[文]若方程=1表示的曲线是双曲线，则实数k的取值范围是（　　 ）

（A）k＜0　　  （B）0＜k＜2　　 （C）k＞2　　　（D）k＞2或k＜0

5. 设抛物线x²=4y的焦点为F，点M在此抛物线上，且 MF =5，则点M到x轴的距离是（　　 ）

（A）2　　　　 （B）3　　　　　 （C）4　　　　  （D）5

6. 复数z=（m-1）+（2-m）i（m∈R）的共轭复数的对应点位于复平面内的第四象限，则实数m的取值范围是（　　　）

（A）1＜m＜2　 （B）m＞2　　　 （C）m＜1　　  （D）m＞2或m＜1

7. 设“P_n^m”和“C_n^m”分别表示从n个不同元素中取出m（m≤n）个元素的排列数和组事数，关于它们有如下论断：

①P_nⁿ=C_nⁿ=1；　　②P_n^m=C_n^mP_m^m；　　③C_n^m+c_n^m-1=C^m_n+1　 ④C_n+1^m+1=C_n^m.

其中全部正确的论断为（　　 ）

（A）①、②、④　 （B）②、③　　 （C）②、③、④　　 （D）③、④

　　　　　　  x=-t⁼²-1,

8. [理]抛物线　　　　　  （t为参数）的焦点坐标是（　　　）

y=t+1

（A）（-，1）　　 （B）（-，1）　（C）（-1，）　　 （D）（-1，）

[文]抛物线（x+1）²=-4（y-1）的准线方程是（　　 ）

（A）x=-2　　　 　（B）x=0　　　　  （C）y=2　　　　  （D）y=0

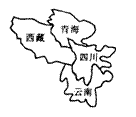
9. 如右图，用红、黄、蓝、绿四种颜色四川、青海、西藏、云南四省（区）

的地图上色，要求每一省（区）只涂一种颜色，并且相邻的省（区）涂不同

颜色，则不同的上色方案有（　　 ）

（A）64种　　　　（B）48种

（C）36种　　　　（D）24种

10. 等比数列{a_n}的前n项和是S_n，{a_n}的公比为q，且S_n=q，则a₁的取值范围是（　　 ）

（A）（-∞，]　　 （B）（-∞，0）∪（0，]

（C）（-2，]　　　（D）（-2，0）∪（0，]

二、填空题：（本大题共4个小题，每小题3分，共12分，把答案填在题中横线上）

11. 设双曲线的半焦距为c，两条准线间的距离为d，且c=d，则双曲线的离心率是　　　 .

12. 若z∈C且 z =1，则 z –2i 的最大值是　　　　　　　　　  .

13. 过坐标原点O作倾斜角为的直线与抛物线y²=-2x交于点A，则线段AO的中点坐标为　　　　　　　　  .

14. 数列{a_n}和{b_n}的通项公式分别是a_n=2ⁿ，b_n=3ⁿ（n∈N），关于这两个数列有如下论断：

①数列{a_n}和{b_n}均为等比数列；　　　 ②数列{a_n+b_n}为等比数列；

③；　　　　　　 ④存在m∈N，使用权得=4成立.

其中正确论断的序号是　　　　  （将全部正确论断的序号都填上）.

三、解答题：（共6个小题，满分48分）

15. （本小题满分7分）

已知双曲线的两条渐近线方程为x±y=0，一个焦点坐标是（0，-2），求此双曲线方程.

16. （本小题满分7分）

已和复数z₁=（a²-3）+（2a+1）i，z₂=（a-1）+（a+3）i，（其中a∈R）.z₁、z₂在复平面上分别对应向量、（O为原点）.

（Ⅰ）写出向量对应的复数z；

（Ⅱ）若复数z是纯虚数，求实数a的值.

17. （本小题满分8分）

是否存在常数a，b，使得等式1²+3²+5²+…+（2n-1）²=（an²+b）对任意自然数n均成立？证明你的结论.

18. （本小题满分9分）

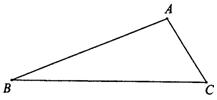
如下图，已知B、C是两个定点，且 BC =8，动点A满足 AB - AC =4.

（Ⅰ）建立适当的坐标系，求动点A的轨迹方程；

（Ⅱ）在（Ⅰ）中的曲线上是否存在点M，使得MB⊥MC成立？如果存在，求出点M的坐标；如果不存在，请说明理由.

19. （本小题满分8分）

已知某市2002年底人口为100万，住房总面积是1000万平方米，如果该市每年人口增长率控制为1%，那么要使2008年初人均住房面积至少达到15平方米，求每年平均新建住房面积至少为多少万平方米？（取1.01⁵=1.051）

20. （本小题满分9分）

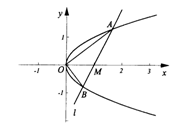如下图，在平面直角坐标系xOy中，点M（1，0）为抛物线y²=x内一定点，经过点M的直线l交抛物线于A（x₁，y₁），B（x₂，y₂）两点.

（Ⅰ）求证：y₁y₂=-1；

（Ⅱ）求证：OA⊥OB；

（Ⅲ）当△AOB的面积是时，求直线l的方程.

四、本题为附加题，成绩计入总分.

21. （本小题满分10分）

已知点列A_n（x_n，0），n∈N，其中x₁=0，x₂=a（a＞0），A₃是线段A₁A₂的中点，A₄是线段A₂A₃的中点，…，A_n是线段A_n-2A_n-1的中点，….

（Ⅰ）写出x_n与x_n-1、x_n-2之间的关系式（n≥3）；

（Ⅱ）设a_n=x_n+1-x_n.计算a₁，a₂，a₃，由此推测数列{a_n}的通项公式，并加以证明；

（Ⅲ）求x_n的值.