数学培训4
第Ⅰ卷
一、选择题（本大题共12小题，每小题5分，共60分。每题有且只有一个正确选项。）：
1. 不等式
＜（
）3(x-1)的解集是（ ）
（A）{xx＞2,或x＜-3} （B）{xx＞3,或x＜-2}
（C）{x-2＜x＜3} （D）{x-3＜x＜2}
2. 欲使cosα-
sinα=
有意义，则m取值范围（ ）
（A）（-∞，-
] （B）[-1，+∞） （C）[-1，]
（D）（-∞，-1）]∪[，+∞）
3. 对于一切实数x，若x-3+x+2＞a恒成立，则a的取值范围是（ ）
（A）a≥5 （B）a＞5 （C）a≤5 （D）a＜5
4. 若方程（6a2-a-2）x+（3a2-5a+2）y+a-1=0表示平行于y轴的直线，则a为（ ）
（A）1或
（B）
（C）1
（D）不存在
5. 直线L:x-2y+2=0绕点A（-2，0）逆时针旋转45°所得的直线方程为（ ）
（A）3x-y+6=0 （B）3x+y+6=0 （C）x-3y-2=0 （D）3x-y-6=0
6. 使不等式x+1＜2x成立的充分不必要条件是（ ）
（A）-
＜x＜1 （B）x＞-
（C）x＞1 （D）x＞3
7. 直线有斜率是直线有倾斜角的（ ）
（A）充分不必要条件 （B）必要不充分条件 （C）充要条件 （D）既不充分又不必要条件
8. 如果实数x,y满足等式（x-2）2+y2=3，那么
的最大值是（ ）
（A）
（B）
（C） （D）
9. 已知点P（a，1），圆C：x2+ax+y2-1=0，则点P与圆C的位置关系是（ ）
（A）在圆内 （B）在圆上 （C）在圆外 （D）无法确定
10. 若集合P={（x,y）y=a（x-1）+2}，Q={（x,y）y=x}，P∩Q为单元素集，则a的取值范围是（ ）
（A）a≤-1或a=2 （B）a≥1或a=2
（C）-1≤a≤1或a=2 （D）-1≤a＜1或a=2
11. 两圆相交于两点（1，3）和（m，-1），两圆圆心都在直线x-y+c=0上，m+c的值是（ ）
（A）-1 （B）2 （C）3 （D）0
12. 已知直线过点M（-3，-），且被圆x2+y2=25截得弦长为8，则这条直线的方程为（ ）
（A）3x+4y+15=0 （B）x+3=0 （C）3x+4y+15=0或x+3=0 （D）以上都不对
Ⅱ卷
二、填空题（本大题共6小题，每小题5分，共30分，把答案填在题中横线上）：
13. 设实数x,y满足x2+（y-1）2=1，当x+y+c≥0时，c的取值范围是 。
14. A、B是x轴上两点，点P的横坐标为2，且PA=PB，若直线PA的方程为x-y+1=0，则直线PB的方程为 。
15. 若方程log
x=
在区间（0，1）上有解，则a的范围是
。
16. 若直线y=x+m与曲线x=
只有一个公共点，则m取值范围为
.
x=2cosθ
17. 一个圆的参数方程为 （θ为参数），一条直线的方程为
y=2sinθ 3x-4y-9=0，
则这条直线与圆的位置关系是 。
18. 已知f（x）=ax2-c且-4≤f（1）≤-1，-1≤f（2）≤5，则f（3）的取值范围是 。
三、解答题（本大题共5小题，每小题12分，共60分）
19. 解不等式：
＜2
20. 直线l过点P（1，-1）经y轴反射后与圆C；（x-4）2+（y-4）2=1相切，求光线在的直线方程。
21. 某厂生产A、B两种产品，需甲、乙、丙三种原料，每生产一吨产品需耗原料如下表甲原料200吨，乙原料360吨，丙原料300吨，若产品生产后能全部销售，试问A、B各多少吨能获最大利润.
| 甲 | 乙 | 丙 | 利润（万元/吨） | |
| A产品 | 4 | 9 | 3 | 7 |
| B产品 | 5 | 4 | 10 | 12 |
22. 已知方程x2+y2-2acosθ·x-2asinθ·y=a2sin2θ。
（1）求证：对于任何θ，方程所表示的曲线是圆。
（2）当a不变，变化θ时，求圆心的轨迹方程。
（3）求证：当a不变时，不论θ为何值，圆在x轴上所截的线段为定长。
23. 直线l:y=mx+1与曲线C：ax2+y2=2（a＞0）交于A、B两点，以OA、OB为邻边作平行四边形OAPB（O为坐标原点）
（1）当a=2时，求点P的轨迹方程；
（2）当a,m满足a+2m2=1，且记平行四边形OAPB的面积函数S（a），
求证：2＜S（a）＜4.
高二数学期中试卷参考答案
一、选择题：
1. D 2. C 3. D 4. D 5. A 6. D 7. A 8. C 9. D 10. D 11. C 12C
二、填空题：
13. c≥-1+
14. x+y-5=0
15. （0，1）
16. m=-或-1＜m≤1
17. 相交
18. –1≤f（x）≤20
19. 解：{xx＜-3或-1＜x＜或x＞1}
20. 解：4x+3y-1=0或3x+4y+1=0
21. 解：设生产A产品X吨，B产品y吨，利润为z.
则z=7x+12y
4x+5y≤200
9x+4y≤360
由条件可知 3x+10y≤300（8分）
x≥0
y≥0
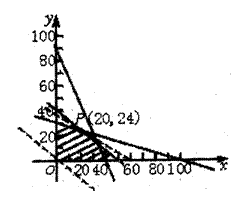
如图，将y=-
x+
平移
4x+5y=200
可知
P（20，24）（10分）
3x+10y=300
即x=20,y=24时z最大.（12分）
22. （1）（略） （2）x2+y2=a2 （3）2a
23. （1）解：设P（x,y），则OP中点为E（
）
y=mx+1
由
2x2+y2=2
消去y得（2+m2）x2+2mx-1=0
设A（x1，y1），B（x2，y2）
则
即AB的中点为E（-
，
）
于是
消去m，得点P的轨迹方程为2x2+y2-2y=0
y=mx+1
（2）证明：由
ax2+y2=2
消去y得
（a+m2）x2+2mx-1=0
进一步就可以求出AB=
·
∵O到AB的距离d=
·S（a）=ABd==
∵a+2m2=1
∴0＜a＜1
∴2＜S（a）＜4