数学培训6
第Ⅰ卷(选择题,共42分)
一、选择题 (本大题共10个小题,其中1~8每小题4分,9~10每小题5分,共42分。在每小题给出的四个选项中,只有一项是符合题目要求的。)
1、若![]() ,则下列不等式(1)
,则下列不等式(1)![]() (2)
(2)![]() (3)
(3)![]()
(4)![]()
![]() 中恒成立的不等式的个数为( )
中恒成立的不等式的个数为( )
(A) 3 (B) 2 (C) 1 (D) 0
2、能表示右图中阴影部分的二元一次不等式组的是( )
 (A)
(A)![]()
(B)![]()
(C)
(D)
3、如果![]() ,且
,且![]() ,则直线
,则直线![]() 不通过( )
不通过( )
(A) 第一象限 (B) 第二象限 (C) 第三象限 (D) 第四象限
4、过![]() 的圆
的圆![]() 的切线方程是( )。
的切线方程是( )。
(A) ![]() (B)
(B)
![]() 或
或![]()
![]()
(C) ![]() (D)
(D)
![]()
5、中心在原点,准线方程为![]() ,离心率为0.5的椭圆标准方程为( )
,离心率为0.5的椭圆标准方程为( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
6、直线![]() 和
和![]() 互相垂直, 则
互相垂直, 则![]() 的值为( )
的值为( )
(A)-![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
7、不等式![]() 的解集是
的解集是  ,则
,则![]() 的值为( )
的值为( )
(A) 14 (B) -14 (C) 10 (D) -10
8、在![]() 轴上截距为
轴上截距为![]() ,且到原点的距离是
,且到原点的距离是![]() 的直线方程为( )
的直线方程为( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]() 或
或![]()
9、若a,b∈R+,a+b=1,则ab+![]() 的最小值为( )
的最小值为( )
(A)2 (B)![]() (C)
(C)![]() (D)
(D)![]()
10、已知两点M(1,![]() )、N(-4,-
)、N(-4,-![]() ),给出下列曲线方程:
),给出下列曲线方程:
①![]() ②
②![]() ③
③![]() ④
④![]()
在曲线上存在点P,满足MP=NP的所有曲线方程是( )
(A)①③ (B)②③ (C)②④ (D)②③④
第Ⅱ卷(非选择题,共78分)
二、填空题(本大题共4小题,每小题4分,共16分。)
11、点![]() 在直线
在直线 ![]() 上移动,则
上移动,则![]() 的最小值是_______________.
的最小值是_______________.
12、直线![]() 关于直线
关于直线![]() 对称的直线方程为_____________.
对称的直线方程为_____________.![]()
13、若椭圆![]() 的焦距为2,则m的值为
.
的焦距为2,则m的值为
.![]()
14、圆与![]() 轴切于(0,6),且
轴切于(0,6),且![]() 轴被圆所截得的弦长为16,那么该圆的方程是_________________.
轴被圆所截得的弦长为16,那么该圆的方程是_________________.
三、解答题 (本题共6小题,共62分。解答应写出文字说明,证明过程或演算步骤。)
15、(满分8分)解不等式 ![]()
16、(满分10分)一个圆的圆心在直线2x+y=0上,并且和两条直线4x-3y+10=0,4x-3y-30=0都相切,求圆的方程
17、(满分10分)咖啡馆配制两种饮料。甲种饮料每杯含奶粉9g、咖啡4g、糖3g;乙种饮料每杯含奶粉4g、咖啡5g、糖10g。已知每天原料的使用限额为奶粉3600g、咖啡2000g、糖3000g。如果甲种饮料每杯能获利0.7元,乙种饮料每杯能获利1.2元,每天在原料的使用限额内饮料能全部售出,每天应配制两种饮料各多少杯能获利最大?
18、(满分10分)![]() ,求证:
,求证:![]()
19、(满分12分)求以坐标轴为对称轴,且过点![]() 和
和![]() 的椭圆的标准方程。并指明
的椭圆的标准方程。并指明
⑴椭圆的长轴和短轴的长;
⑵离心率;
⑶焦点坐标;
⑷准线方程。
20、(满分12分)
已知圆![]()
![]()
⑴ 求证:不论![]() 为何值,圆心都在直线
为何值,圆心都在直线![]() :
:![]() 上;
上;
⑵若直线![]() 与
与![]() 平行且与圆相交,求
平行且与圆相交,求![]() 的取值范围;
的取值范围;
⑶求证:任何一条平行于![]() 且与圆相交的直线被圆截得的弦长为定值。
且与圆相交的直线被圆截得的弦长为定值。
数学培训6参考答案
一、 选择题
1—10:ACCBA DBDCB
二、 填空题.
11、
8 12、![]()
13、![]() 14、
14、![]()
三、 解答题.
15、解:原式可化为 ![]()
![]()
不等式的解集为![]()
16、解:两条平行线的距离为![]()
![]() 圆的半径为
圆的半径为![]()
由 解得
解得
![]() 圆心坐标为
圆心坐标为![]()
![]() 圆的方程为
圆的方程为![]()
17、解:设每天应配制甲种饮料![]() 杯,乙种饮料
杯,乙种饮料![]() 杯,
杯,
咖啡馆每天获利![]() (元)
(元)
![]() ,
,![]() 满足约束条件
满足约束条件
在平面直角坐标系内做出可行域,作直线![]()
由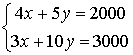 得最优解
得最优解![]()
所以每天应配制甲种饮料200杯,乙种饮料240杯,才能使咖啡馆每天获利最大。
18、解:设椭圆方程为![]()
![]()
将![]() ,
,![]() 代入,
代入,
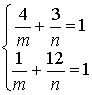 解得
解得 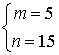
![]() 椭圆方程为
椭圆方程为![]()
⑴椭圆的长轴长![]() ,短轴的长
,短轴的长![]()
⑵离心率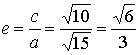
⑶焦点坐标![]() ,
,![]()
⑷准线方程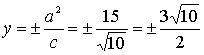
19、证明:![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
原不等式得证。
20、解:⑴、将圆配方得![]()
设圆心为![]() ,则
,则
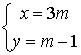 消
消![]() 得:
得: ![]()
![]() 圆心恒在直线
圆心恒在直线![]() 上
上
⑵、设与![]() 平行的直线为
平行的直线为![]()
圆心![]() 到直线
到直线![]() 的距离
的距离

![]() 半径
半径![]()
![]() 当
当![]() 即
即![]() 时,直线与圆相交
时,直线与圆相交
⑶、对于任一条平行于![]() 且与圆相交的直线
且与圆相交的直线![]()
圆心到直线![]() 的距离
的距离![]()

![]() 弦长
弦长![]() 与
与![]() 无关,故截得弦长为定值
无关,故截得弦长为定值