高二数学测练（第15周）(双曲线)
一、选择题：（每题4分共60分）
1.已知双曲线
,那么它的半焦距等于( b )
A.
B.10 C.
D.4
2.双曲线
上的点P到点(5,0)的距离为15,则P到点(—5，0)的距离是( d )
A.7 B.23 C.25或7 D.7或23
3.已知方程
,若实数
异号,则它的图象是( d
)
A.椭圆,焦点在
轴上 B.双曲线,焦点在轴上
C.椭圆,焦点在
轴上
D.双曲线,焦点在轴上
4.已知点
,曲线上的动点P到
的距离减去P到
的距离的值为6,则曲线方程为( a )
A. 
B.
C.
D.
5.双曲线的焦点在轴上，且它的一个焦点在直线
上，两焦点关于原点对称,
,则此双曲线的方程是( d )
A.
B.
C.
D.
6.若双曲线
-
=l上一点P到它的右焦点的距离为4，则点P到它的左准线的距离为( c
)
A．
B．4 C．
D．8或
7．过双曲线x2－
=1的右焦点F作直线l交双曲线于A, B两点，若AB=4，则这样的直线l有
（ ）
A.1条 B.2条 C.3条 D.4条
8．过双曲线
的右焦点F2作垂直于实轴的弦PQ, F1是左焦点, 若∠PF1Q=900,
则双曲线的离心率为
( )
A. 
B. 1+ C.
2+ D.
3-
9．已知m,n为两个不相等的非零实数，则方程mx－y+n=0与nx2+my2=mn所表示的曲线可
能是 （ c ）
A B C D
10．双曲线kx2+4y2=4k的离心率小于2，则k的取值范围是 （ ）
A. (－12, 0) B.(－3, 0) C.(－∞, 0) D.(－60, －12)
11．与曲线
共焦点，而与曲线
共渐近线的双曲线方程为 （ ）A．
B．
C．
D．
12.已知双曲线b2x2－a2y2 = a2b2的两渐近线的夹角为
，则离心率e为 （ c ）
A.
B.
C.
D.
二.填空题:(每题4分共16分)
13.方程
，若它表示椭圆，则
满足的条件是______________,若它表示双曲线,则满足的条件是______________;.
14.已知平面内有一条线段
,
,动点
满足
的中点,则
的最小值为________________;3/2
15、已知双曲线的渐近线方程是y=±
x，则此双曲线的离心率是_______
或
16. 如图, 直线l ^ FH于H, O为FH的中点, 曲线C1 , C2是以F为焦点, l为准线的圆锥曲线(图中只画出曲线的一部分）, 那么圆锥曲线C1是 ; 圆锥曲线C2是 .
 |
椭圆 ; 双曲线
三、解答题(本大题共6小题，共74分)
17.(12分)已知双曲线与椭圆
+
=1共焦点，它们的离心率之和为
，求双曲线方程．
解：椭圆+=1的焦点为(0，4)，(0，-4),
由题意设双曲线方程为
-
=l(a>0，b>0),则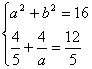
∴a=2,b2=12, ∴所求的双曲线的方程为
-
=1．
18．（12分）直线y=x+b与双曲线2x2－y2=2相交于A, B两点，若以AB为直径的圆过原点，求b的值．
19．（12分）双曲线 (a>1,b>0)的焦距为2c,直线l过点(a,0)和(0,b),且点(1,0)到直线l的距离与点(-1,0)到直线l的距离之和s≥
c.求双曲线的离心率e的取值范围.
20.（12分）ΔABC的底边BC=2a,其它两边的斜率之积等于
(a>0,b>0),求顶点A的轨迹方程.
21（12分）．设双曲线中心是坐标原点，准线平行于x轴，离心率为
，已知点P（0，5）到这双曲线上的点的最近距离是2，求双曲线方程。
解：提示：设双曲线的方程为
（a>0，b>0）
∵
∴a=2b，所以设所求双曲线方程为
设Q（x，y）为双曲线上一点，则
其中y≥2b
当2b≤4时，应有y=4时
，从而
，即
，方程为
当2b>4时，应有y=2b时，，从而
，所以
或
（与b>2矛盾），所以方程为
22．（14分）已知直线y=ax+1与双曲线
相交于A、B两点，是否存在这样的实数a，使得A、B关于直线y=2x对称？如果存在，求出a的值，如果不存在，说明理由。