德州市高二年级期末考试（文科）

德州市2005-2006学年度高二年级期末考试

高二文科试题

一、选择题

1、若命题p的逆命题为q，命题q的否命题为r，则p是r的（　　）

　A、逆命题　 B、否命题　　　　　　　　　　C、逆否命题　　　　　　　D、以上均不对

2、复数z对应的点在第二象限，它的模为3，实部是，则是　　　　　  （　 ）

（A）+2i　　 （B）-2i　　（C）+2i　　（D）-2i

3、下列说法正确的是（　　）

 A、若a＞b，c＞d，则ac＞bd　　　　　B、若，则a＜b

C、若b＞c，则a·b≥a·c　　　　　　D、若a＞b，c＞d，则a-c＞b-d

4、命题甲：平面内动点P到两定点A、B的距离之和为PA+PB=2a（a>0且为常数）；命题乙：P点的轨迹是以A、B为焦点的椭圆，则命题甲是命题乙的　　　　　　　　　　　　　　　 （　　 ）

（A）充分不必要条件　　　　　　　　  （B） 必要不充分条件　　　　　 

（C）充要条件　　　　　　　　　　　  （D） 既不充分也不必要条件

5、三角形ABC中，sinA：sinB：sinC=4：3：2则cosA的值　　　　　　　　　　  （　　）

（A）-　　  （B）　　 （C）-　　（D）

6、已知双曲线x²-4y²=4上一点到双曲线一个焦点的距离为6，那么到另一个焦点的距离等于（　）

（A）10（B）6±2（C）6+2（D）10或2

7、等差数列{a_n}中，若a₁₀=10，a₁₉=100，前n项和S_n=0，则n=（　　）

　　A、7　　　　　　　　　　B、9　　　　　　　　　　C、17　　　　　　　　　D、19

8、椭圆+y²=1的两个焦点为F₁、F₂，过F₁作垂直于x 轴的直线与椭圆相交，一个交点为P，则PF₂等于（　）

（A）（B）（C）（D）4

9、数列{a_n}的前n项和S_n=3ⁿ-C，则当C为何值时{a_n}为等比数列（　　）

A、1　　　　　　　　　　B、2　　　　　　　　　　C、3　　　　　　　　　　D、4

10、抛物线y=ax²的准线方程是y=2，则a的值　　　　　　　　　　　　　　　　　 （　 ）

（A）　　　 （B）-（C）8（D）-8

11、平面上的n个圆，每两个圆都相交，每三个圆都不相交于一点，则它们把平面分成（）部分

　　A、n²-n+2　　　　　　B、n²+n　　　　　　　 C、n²-2n+3　　　　　D、n²+2n-1

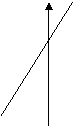
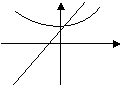
12、已知曲线与直线mx+ny+1=0在同一直角坐标系中，它们的图形可能是 （　）

y

y

　 　　　y　　　　　　　　　　　　　　　  　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 

x　　　　　　　　 x　　　　　　　　　　　 x　　　　　　　　 x

　　　 (A)　　　　　　　　　　  (B)　　　　  　　　　　　　(C)　　　　　 (D)

二、填空题

13、x、y∈R，，则xy=　　　　　 　　 

14、三角形ABC中，已知A（-2，0）、B（2，0），且AC、AB、BC三边成等差数列 ，则点C的轨迹方程为 　　　　　　　　　　  

15、一同学在电脑中打出如下图若干个圆（○表示空心圆，●表示实心圆）

○●○○●○○○●○○○○●○○○○○●○……

问：到2006个圆中有　　　 　　　　 个实心圆。

　　16、方程表示的曲线为C，给出下列四个命题①曲线C不可能是圆，②若1＜t＜4则曲线C为椭圆，③ 若曲线C为 双曲线，则t＜1或t＞4④ 若曲线C表示焦点在x轴上的椭圆则1＜t＜，其中正确的命题序号是　　　　　

三、解答题

17、三个实数a、b、c成等差数列且a+b+c=9又a+1、b+3、c+13成等比数列，求a、b、c的值。

18、已知定圆F₁：x²+y²+10x+24=0，定圆F₂：x²+y²-10x=0，动圆M与定圆F₁、F₂都外切，求动圆圆心M的轨迹方程。

19、设z₁=1+2ai，z₂=a-i（aR），已知A={zz-z₁≤1}，B={zz-z₂≤2}，AB=，求a的取值范围

20、有一印刷品排版面积（矩形）为432cm²，左右各留4cm的空白，上下各留3cm空白，问应如何选择纸张尺寸，才能使纸张的面积最少.

21、在△ABC中，a、b、c分别为∠A、∠B、∠C的对边，如果a、b、c成等差数列

∠B=60°，△ABC的面积为，求b。

22、设双曲线的焦点分别为F₁、F₂，离心率为2。

（1）求此双曲线的渐近线l₁、l₂的方程；

（2）若A、B分别为l₁、l₂上的动点，且2AB=5F₁F₂，求线段AB的中点M的轨迹方程，并说明轨迹是什么曲线。

答案：一、选择题：CBCBA　DCCAB　AC

　　　二、填空题：13．5　　14． （y≠0）15、61　16、③④

　　　三、解答题：

 17、解：有题设可得：

a+c=2b

a+b+c=9

（a+1）（c+13）=（b+1）²　　　　　　　　　　　 ……6分

　　　　得 a=1 ，b=3,c=5或　a=17, b=3,c=-11　　　　　　　  ……12分

　　　　  18、解：由x²+y²+10x+24=0可知(x+5)²+y²=1　∴圆心为（-5，0），r₁=1

由x²+y²-10x=0　　即(x-5)²+y²=25　 ∴圆心为（5，0），r₂=5……4分

∵ MF₁=R+r₁=R+1，MF₂=R+r₂=R+5

∴MF₂-MF₁=4　　 即M的轨迹为双曲线一支……8分

∵2a=4　　∴a=2　　　　又∵ c=5　 ∴

∴（x＜0　　…………12分

（注：没有x＜0的减1分

19、解：∵A表示以z₁为圆心，1为半径的圆的内部（含边界）

B表示以z₂为圆心，2为半径的圆的内部（含边界）…………4分

∵AB=　　 ∴z₁z₂＞3………………8分

∴z₁z₂²＞9　　即(1-a)²+(2a+1)²＞9

即　 a〉1 或　a〈-　　………………12分

 20、设版面左右为x㎝，则上下长㎝，

那么纸的左右为（x+8）㎝，上下为（+6）㎝。

纸张的面积S=（x+8）（+6）=480+6x+（8×）

当且仅当6x=8×　即x=18时，S取最大值 ，此时=24

所以纸张左右为24+8=32（㎝），上下宽为18+6=24（㎝）

21、解：S_△=acsinB=　　　　 即ac·=　　 ∴ac=6　…………4分

由余弦定理：b²=a²+c²-2accosB=(a+c)²-2ac(1+cosB)

　　即：　b²=(a+c)²-12(1+)………………8分

　 将代入上式　　得b²=6

　　 ∴b=　 ………………12分

22、解：（1）∵

∴双曲线方程为　

∴其渐近线方程式为y=…………6分

（2）∵　 ∴c=2　即F₁F₂=4

∵2AB=5F₁F₂　　　　∴AB=10　………………8分

设A（x₁，）　 B（x₂，），中点M（x，y）

则x₁+x₂=2x，　 x_1­-x₂=　 …………10分

∵AB=10　　即(x₁-x₂)²+(x₁+x₂)²=100

即　

∴M的轨迹是焦点在x轴上的椭圆………………14分