第一学期期末联考模拟试卷

宁波市2005学年第一学期期末联考模拟试卷(1)

时间：90分钟，满分120分.

班级_______________姓名______________________

一、选择题

1、教室内有一直尺，无论怎样放置，在地面总有直线与直尺所在直线　　　　　  (　　)

 A、平行　　　　  B、垂直　　　　  C、相交　　　　  D、 异面

2、过点（2,1）的直线中，被截得的最长弦所在的直线方程是　 （　　）

A、3x-y-5=0　　B、3x+y-7=0　　　 C、x+3y-5=0　　 D、x-3y+1=0

3、已知是三角形的一个内角，且，则方程表示（　　）

  A、焦点在轴上的椭圆　　　　　　　　  B、焦点在轴上的椭圆

　C、焦点在轴上的双曲线　　　　　　　  D、焦点在轴上的双曲线

4、已知P是△ABC所在平面外一点，且PA = PB = PC，则P在上的射影一定是△ABC的　　 （　　）

 A、内心　　　　 B、外心　　　　 C、重心　　　　 D、垂心

5、设F₁、F₂是双曲线的两个焦点，点P在双曲线上，∠F₁PF₂=90°若△F₁PF的面积为1，则a的值是　　　 （　　）

A、1　　　　　  B、　 　　　C、2　　　　　  D、

6、与圆：相切且在、轴上截距相等的直线有　　　 (　　)

 A、条　　　　 B、条　　　　 C、条　　　　  D、条

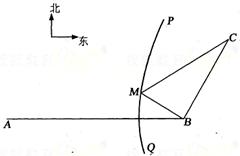
7、如图，B地在A地的正东方向4 km处，C地在B地的

北偏东30°方向2 km处，河流的没岸PQ（曲线）上任意

一点到A的距离比到B的距离远2 km.现要在曲线PQ上选

一处M建一座码头，向B、C两地转运货物。经测算，从

M到B、M到C修建公路的费用分别是a万元/km、

2a万元/km，那么修建这两条公路的总费用最低是 （　　）

A、(2－2)a万元　B、5a万元　C、(2+1)a万元 　D、(2+3)a万元

8、直线与圆的位置关系是　　　　　　　　 (　　)

  A、相交　　 　　B、相离　　　　 C、相切　　　　D、与、的取值有关

9、设、，集合，，若为单元素集，则值的个数是　　　　　　　　  （　　）

　A、　　　 　　 B、　　 　　　 C、　　　　　　D、

10、双曲线的两个焦点为，以为边作等边三角形，若双曲线恰平分三角形的另两边，则双曲线的离心率为　　　　　 （　　）

A、　　  　B、　　  　C、　　 　D、

二、填空题

 11、若双曲线与圆有公共点，则实数的取值范围为___________。

12、已知正方体的棱长为1，则过A₁C₁且与BD₁平行的截面面积为___________。

13、直线的方程为，在上任取一点P，若过点P且以双曲线的焦点作为椭圆的焦点，那么具有最短长轴的椭圆方程为________________________。

14、正方形ABCD的两对角线AC与BD交于O，沿对角线BD折起，使∠AOC=90对于下列结论：①AC⊥BD；②△ADC是正三角形；③AB与CD成60角；④AB与平面BCD成60角，其中正确的结论是_____________________。

三、解答题

15、设有编号为1，2，3，4，5的五个球和编号为1，2，3，4，5的五个盒子，现将这五个球放入5个盒子内

（1）只有一个盒子空着，共有多少种投放方法？

（2）没有一个盒子空着，但球的编号与盒子编号不全相同，有多少种投放方法？

　 （3）每个盒子内投放一球，并且至少有两个球的编号与盒子编号是相同的，有多少种投放方法？

16、已知双曲线和椭圆：有公共的焦点，它们的离心率分别是和，且，求双曲线的方程．

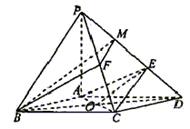
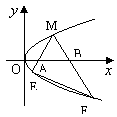17.如图，M是抛物线上y²=x上的一点，动弦ME、MF分别交x轴于A、B两点，且MA=MB.

　 （1）若M为定点，证明：直线EF的斜率为定值；

　 （2）若M为动点，且∠EMF=90°，求△EMF的重心G的轨迹

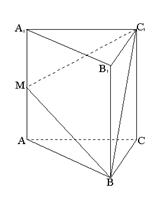
18、 如图，在正三棱柱中，，由顶点B沿棱柱侧面经过棱到顶点的最短路线与的交点记为M，求：

　 （I）求证：平面平面

（II）平面与平面ABC所成二面角（锐角）的大小

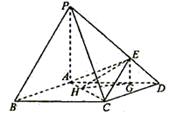
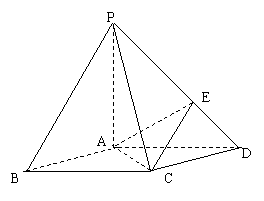
19、如图，在底面是菱形的四棱锥P—ABCＤ中，∠ABC=60⁰，PA=AC=a，PB=PD=,点E在PD上，且PE:ED=2:1.

（I）证明PA⊥平面ABCD；

（II）求以AC为棱，EAC与DAC为面的二面角的大小；

（Ⅲ）在棱PC上是否存在一点F，使BF//平面AEC？证明你的结论.

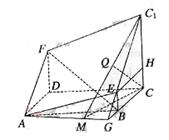
20．（本小题满分12分）

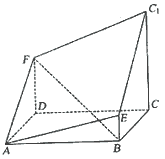
　　如图所示的多面体是由底面为ABCD的长方体被截面AEC₁F所截面而得到的，其中AB=4，BC=2，CC₁=3，BE=1.

　 （Ⅰ）求BF的长；

　 （Ⅱ）求点C到平面AEC₁F的距离.

参考答案：

BABBA，CBADA，

11、， 12、， 13、，14、①2③

15、（1）C₅²A_­5⁴=1200（种）　　　　　　　　  ……4分

（1）A₅⁵-1=119（种）　　　　　　　　　　　 ……8分

（2）不满足的情形：第一类，恰有一球相同的放法：

　　 C₅¹×9=45

第二类，五个球的编号与盒子编号全不同的放法：

　　

∴ 满足条件的放法数为：

　　A₅⁵-45-44=31（种）　　　　　　　　　  ……12分

16

解：（1）设M（y,y₀），直线ME的斜率为k(l>0)

则直线MF的斜率为－k，方程为

∴由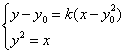，消

解得

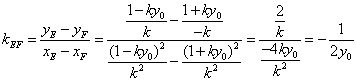∴(定值)

所以直线EF的斜率为定值

（2）直线ME的方程为

由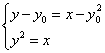得

同理可得

设重心G（x, y），则有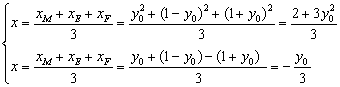

消去参数得

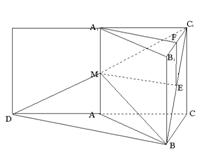
18、如图，在正三棱柱中，AB＝2，，由顶点B沿棱柱侧面经过棱到顶点的最短路线与的交点记为M，求：

　　（I）求证：平面平面

（II）平面与平面ABC所成二面角（锐角）的大小

解：（I）如图，将侧面绕棱旋转使其与侧面在同一平面上，点B运动到点D的位置，

连接交于M，则就是由顶点B沿棱柱侧

面经过棱到顶点C₁的最短路线，

， M为中点

取BC₁中点E，B₁C₁中点F，连ME，A₁F，EF则有EF∥A₁M，EF=A₁M，∴A₁M EF 是平行四边形ME∥A₁F，又A₁F⊥平面，∴ME⊥平面

∴平面平面　　　 ………………………………6分

（II）连接DB，，则DB就是平面与平面ABC的交线，在中，

 就是平面与平面ABC所成二面角的平面角（锐角）……10分

中，，。……12分

19、（本小题满分12分）

如图，在底面是菱形的四棱锥P—ABCＤ中，∠ABC=60⁰，PA=AC=a，PB=PD=,点E在PD上，且PE:ED=2:1.

（I）证明PA⊥平面ABCD；

（II）求以AC为棱，EAC与DAC为面的二面角的大小；

（Ⅲ）在棱PC上是否存在一点F，使BF//平面AEC？证明你的结论.

解：（Ⅰ）证明　因为底面ABCD是菱形，∠ABC=60°，

所以AB=AD=AC=a，　在△PAB中，由PA²+AB²=2a²=PB²所以PA⊥AB.

同理，PA⊥AD，所以PA⊥平面ABCD. ……4分

（Ⅱ）解　作EG//PA交AD于G，由PA⊥平面ABCD，

知EG⊥平面ABCD.作GH⊥AC于H，连结EH，则EH⊥AC，

∠EHG即为二面角的平面角.

又PE : ED=2 : 1，所以

从而  　…………8分

（Ⅲ）当F是棱PC的中点时，BF//平面AEC，证明如下：

 取PE的中点M，连结FM，则FM//CE.　①

由　 知E是MD的中点.

连结BM、BD，设BDAC=O，则O为BD的中点.

所以　BM//OE.　②

由①、②知，平面BFM//平面AEC.

又　BF平面BFM，所以BF//平面AEC……12分

20．本小题主要考查线面关系和空间距离的求法等基础知识，同时考查空间想象能力和推理运算能力.

解法1：（Ⅰ）过E作EH//BC交CC₁于H，则CH=BE=1，EH//AD，且EH=AD.

又∵AF∥EC₁，∴∠FAD=∠C₁EH.

∴Rt△ADF≌Rt△EHC₁.　∴DF=C₁H=2.

（Ⅱ）延长C₁E与CB交于G，连AG，

则平面AEC₁F与平面ABCD相交于AG.

过C作CM⊥AG，垂足为M，连C₁M，

由三垂线定理可知AG⊥C₁M.由于AG⊥面C₁MC，且

AG面AEC­₁F，所以平面AEC₁F⊥面C₁MC.在Rt△C₁CM中，作CQ⊥MC₁，垂足为Q，则CQ的长即为C到平面AEC₁F的距离.

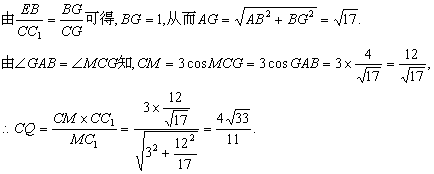
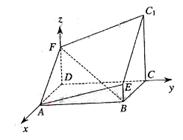
解法2：（I）建立如图所示的空间直角坐标系，则D（0，0，0），B（2，4，0），A（2，0，0），

C（0，4，0），E（2，4，1），C₁（0，4，3）.设F（0，0，z）.

∵AEC₁F为平行四边形，

（II）设为平面AEC₁F的法向量，

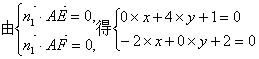
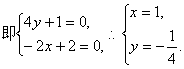
的夹角为a，则

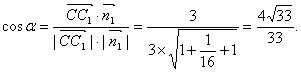
∴C到平面AEC₁F的距离为