第六章 不等式单元检测题
一、选择题（每小题4分，共48分）
1．设a<b<0，则下列不等式中不能成立的是（ ）
A．> B．＞ C．
D．a2>b2
2．若a、b、c、d是任意实数，则下列各结论一定成立的是（ ）
A．a>b,c=d
ac>bd B．＞a>b
C．a3>b3,ab>0< D．a2>b2,ab>0<
3．若a>b>c>1，则abc，ab，bc，ac从小到大的排列顺序是（ ）
A．ac<bc<ab<abc B．ac<bc<abc<ab
C．bc<ac<ab<abc D．bc<ab<ac<abc
4．已知直角三角形的周长为2，则它的最大面积为（ ）
A．3－2 B．3＋2 C．3－ D．3＋
5．已知x>0，y>0，且x≠y，则下列各式中最小的是（ ）
A．(+) B． C．
D．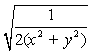
6．已知a、b为正实数，则、、
、
的大小顺序是（ ）
A．
B．
C．
D． 
7．某厂产值第二年比第一年增长p%，第三年比第二年增长q%，又这两年的平均增长率为s%，则s与的大小关系是（ ）
A．s＞ B．s＝ C．s≥ D．s≤
8．下列不等式中，与不等式“x<3”同解的是（ ）
A．x(x+4)2＜3(x+4)2 B．x(x-4)2＜3(x-4)2
C．x+＜3+ D．x+
＜3+
9．关于x的不等式(x-2)(ax-2)＞0的解集为｛x︱x≠2,x∈R｝，则a=( )
A．2 B．-2 C．-1 D．1
10．不等式∣x2-x-6∣>∣3-x∣的解集是（ ）
A．（3，+∞） B．(－∞，-3)∪（3，+∞）
C．(－∞，－3)∪（－1，+∞） D．(－∞，－3)∪（－1，3）∪（3，+∞）
11．设y=x2+2x+5+
，则此函数的最小值为（ ）
A． B．2 C． D．以上均不对
12．若方程x2－2x＋lg(2a2－a)=0有两异号实根，则实数a的取值范围是（ ）
A．(，+∞) ∪(－∞，0) B．(0，)
C．(－，0) ∪(，1) D．(－1，0) ∪(，+∞)
二、填空题（每小题4分，共16分）
13．若x，y为正实数，且2x＋5y＝20，则lgx＋lgy的最大值为＿＿＿＿＿．
14．设x>0，y>0，A＝ 
，B＝
＋
，则A、B大小关系是＿＿＿．
15．如果
对于任意x实数恒成立，则实数a的取值范围＿＿＿＿．
16．若函数
的定义域是R，则实数k的取值范围是＿＿＿．
三、解答题（共4题，共36分）
17．（本题8分）设a、b、c为不全相等的正实数，
求证：
．
18．（本题10分）解不等式
．
19．(本题8分)解关于x的不等式ax2－（a＋1）x＋1＜0（a＞0）．
20．（本题10分）某单位决定投资3200元建一仓库（长方体状）高度恒定，它的后墙利用旧墙不花钱，正面用铁栅，每米长造价40元，两侧墙砌砖，每米长造价45元，顶部每平方米造价20 元，试计算：
①仓库底面积S的最大允许值是多少？
②为使S达到最大，而实际投资又不超过预算，那么正面铁栅应设计多长？
参考答案
一、选择题：
BCCAD CDBDD AC
二、填空题：
13．1 14．A<B 15．（－∞，7） 16．[0，1 ]
三、解答题：
17．略
18．（3，5）
19．略
20．最大允许值为100平方米，此时正面铁栅长为15米。