2005--2006年度株洲市第十七中学高二数学
期终检测题二
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的,请把正确答案的代号填在题后的括号内。(每小题5分,共50分)
1. 已知M=![]() ,N={xx2-5x+6≥0},则集合M与N的关系是( D )
,N={xx2-5x+6≥0},则集合M与N的关系是( D )
A M是N的真子集 ; B M![]() N
C M
N
C M![]() <N D N是M的真子集 .
<N D N是M的真子集 .
2.已知直线L1:ax+by+c=0;L2:mx+ny+d=0,则(am)/(bn)=-1是两直线垂直的(A )
A.充分不必要条件 B.必要不充分条件 C. 充要条件 D.既不充分也不必要条件
3.若对于任意实数![]() ,不等式
,不等式![]() 恒成立,则
恒成立,则![]() 的取值范围是(C)
的取值范围是(C)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 。
。
4.过点P(-2,1)的直线与圆C:![]() 相交于点A、B,若P恰好为AB之中点,则直线AB的方程是( )
相交于点A、B,若P恰好为AB之中点,则直线AB的方程是( )
(A) x+y-1=0 (B) x-y+1=0 (C) x-y-1=0 (D) x+y+1=0。
5.设0<x<1,![]() 为常数,则
为常数,则![]() 的最小值是( B )
的最小值是( B )
A ![]() B
B ![]() C
C ![]() D
D ![]()
6.已知圆(x-3)2+(y-3)2=9与直线3x+4y-11=0,那么圆上的点到直线的距离为1的点有( C )个
A 1 B 2 C ![]() 3 D 4
3 D 4
7.已知椭圆![]() 上的一点P到左焦点的距离为6,则P到右准线的距离是(A )
上的一点P到左焦点的距离为6,则P到右准线的距离是(A )
A 20 B 12 C 5 D 3
8.将进货单价为80元的商品按90元一个售出时能卖出400个,已知这种商品每个上涨1元时,其销售就减少20个,为了赚取最大利润销售价应定为每个( D )元。
A.110 B.105 C.100 D.95。
9、已知双曲线的渐近线方程为![]() ,实轴在坐标轴上,焦距为10,则它的方程是(B )
,实轴在坐标轴上,焦距为10,则它的方程是(B )
A ![]() B
B
![]() 或
或![]() ;
;
C ![]() D
D ![]() 或
或![]()
10、已知直线![]() 交抛物线
交抛物线![]() 于A、B两点,若AB中点的横坐标为2,则AB=( C )。
于A、B两点,若AB中点的横坐标为2,则AB=( C )。
A ![]() ;
B 4
;
B 4![]() ; C 2
; C 2![]() ; D
; D ![]() 。
。
二、填空题:请把答案填在题中横线上(每小题6分,共计30分)。
11、不等式![]() 的解集是_
的解集是_![]() ___.
___.
12、已知圆![]() 与抛物线
与抛物线![]() 准线相切,则
准线相切,则![]() =___2___
=___2___
13、已知![]() ,则函数
,则函数![]() 的最小值是__30___ .
的最小值是__30___ .
14.动点P到直线![]() =4的距离是它到点A(2,0)距离的2倍,则动点P的轨迹方程是
___
=4的距离是它到点A(2,0)距离的2倍,则动点P的轨迹方程是
___![]() .
.
15、已知直线![]() 的方程:
的方程:![]() ,直线
,直线![]() 与
与![]() 关于原点对称,直线
关于原点对称,直线![]() 与
与![]() 关于直线
关于直线![]() 对称,直线
对称,直线![]() 与
与![]() 关于
关于![]() 轴对称,则
轴对称,则![]() 的方程:__
的方程:__![]() _____
_____
三、解答题:解答应写出文字说明、证明过程或演算步骤.(共6小题,计70分)
16、(本题满分10分)
已知关于![]() 的不等式
的不等式![]() 的解集为
的解集为![]() ,解关于
,解关于![]() 的不等式
的不等式![]()
解:因不等式![]() 的解集为
的解集为![]() ,所以
,所以 ![]() ,因此不等式
,因此不等式![]()
解于不等式![]() ,即
,即![]()
所以原不等式的解集是:![]()
17.(本题满分10分) 设抛物线 ![]() 的弦PQ被直线
的弦PQ被直线![]() :x+y-2=0垂直平分,求原点到PQ的距离。
:x+y-2=0垂直平分,求原点到PQ的距离。
解:直线![]() 的斜率
的斜率![]() =-1,设直线PQ的方程为:y=x+b,并代入
=-1,设直线PQ的方程为:y=x+b,并代入![]() 化简得:
化简得:![]()
设P![]() 、Q
、Q![]() ,线段PQ的中点M(
,线段PQ的中点M(![]() ,则由根与系数的关系有
,则由根与系数的关系有![]() ,
,![]() ,
,
又点M在直线PQ上,将M(![]() 代入直线方程中得b=-1,所以直线PQ的方程是:x-y-1=0,所以原点到直线PQ的距离是
代入直线方程中得b=-1,所以直线PQ的方程是:x-y-1=0,所以原点到直线PQ的距离是![]()
18、(本题满分12分) 某厂要将两种大小不同的铝材料截成A、B、C、D四种规格,每张铝材料可同时截得四种规格的小铝材料的块数如下表所示:
| 规格类型 铝材料型 | A | B | C | D |
| 第一种铝材料 | 1 | 1 | 3 | 2 |
| 第一种铝材料 | 2 | 1 | 2 | 3 |
今需A、B、C、D四种规格的成品分别为10块、10块、12块、12块,问截这两种铝材料多少张可得所需四种规格成品,且使用铝材料张数最少?
解:设需第一种铝材![]() 张,需第二种铝材
张,需第二种铝材![]() 张,则可得下列线性约束条件:
张,则可得下列线性约束条件: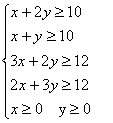
目标函数为铝材的总张数![]() ,易得这两种铝材分别为:(0,10)或(1,9)或(2,8)……
,易得这两种铝材分别为:(0,10)或(1,9)或(2,8)……
或(10,0)可得四种成品规格,且使用的铝材张数最小。
19.(本题满分12分) 自椭圆![]()
![]() 上的一点M向
上的一点M向![]() 轴作垂线,恰好通过椭圆的左焦点F1,且其长轴右端点A及短轴的上端点B的连线AB与OM平行(O为椭圆中心)。
轴作垂线,恰好通过椭圆的左焦点F1,且其长轴右端点A及短轴的上端点B的连线AB与OM平行(O为椭圆中心)。
(1)求此椭圆的离心率;(2)若此椭圆的一条准线方程是![]() =10,求椭圆方程。
=10,求椭圆方程。
提示:易求M![]() ,由AA∥OM得:KAB=KOM,
,由AA∥OM得:KAB=KOM,![]() , 椭圆方程是:
, 椭圆方程是:![]()
![]()
20.(本题满分12 分) 已知直线![]() :
:![]() 与双曲线
与双曲线![]() 的左支交于A、B两点,直线
的左支交于A、B两点,直线![]() 过P(-2,0)和线段AB的中点,求:
过P(-2,0)和线段AB的中点,求:
(1)![]() 的取值范围;(2)
的取值范围;(2)![]() 在
在![]() 轴上的截距
轴上的截距![]() 的取值范围。
的取值范围。
解:由![]() 代入
代入![]() 中,化简得
中,化简得 ![]() ,因两交点在左支上,
,因两交点在左支上,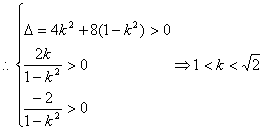 ,设M
,设M![]() 为AB之中点,
为AB之中点,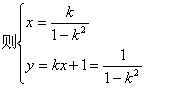
![]() , 又因P、Q
, 又因P、Q![]() 、M都在直线
、M都在直线![]() 上,
上,![]() ,
,
令![]() ,则
,则![]() 上为减函数,
上为减函数,![]()
![]() 。
。
21.(本题满分14分) 设椭圆为![]() ,过点M(0,1)的直线
,过点M(0,1)的直线![]() 交椭圆于A、B两点,O是坐标原点,点P满足
交椭圆于A、B两点,O是坐标原点,点P满足![]() ,点N的坐标是(0.5,0.5),当
,点N的坐标是(0.5,0.5),当![]() 绕点M旋转时,求:(1)动点P的轨迹方程;(2)求NP的最大值与最小值,
绕点M旋转时,求:(1)动点P的轨迹方程;(2)求NP的最大值与最小值,
解:(1) 设P![]() ,又因A
,又因A![]() 、B
、B![]() 在椭圆上,则有
在椭圆上,则有
![]() …………(1)
…………(1) ![]() ………………(2)
………………(2)
由![]() 得
得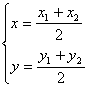 ………………(3)
………………(3)
(1)-(2) 当![]() 得
得 ![]() …………(4)
…………(4)
又![]() …………………………(5)
…………………………(5)
由(4)(5)得 ![]() ………………(6)
………………(6)
当![]() 时,点A、B的坐标分别为((0,2),(0,-2),这时P的坐标为(0,0)也满足(6),
时,点A、B的坐标分别为((0,2),(0,-2),这时P的坐标为(0,0)也满足(6),
所以所求的轨迹方程是:![]()
![]() 。
。
(2)由点P的轨迹方程知![]() ,而NP2=(x-0.52+(y-0.5)2=……=
,而NP2=(x-0.52+(y-0.5)2=……=![]() ,
,
当![]() 。
。