2005~2006年皖南十校高二数学期末联考-人教版[原创]
一、选择题（每题6分，共60分）
1．已知点A为双曲线
的左顶点，点B和点C在双曲线的右支上，
是等边三角形，则的面积是
（ ）
（A）
（B）
（C）
（D）
2．平面上整点（纵、横坐标都是整数的点）到直线
的距离中的最小值是（ ）
（A）
（B）
（C）
（D）
3．若实数x, y满足(x + 5)2+(y – 12)2=142，则x2+y2的最小值为 （ ）
(A) 2
(B) 1
(C) 
(D)
4．直线
椭圆
相交于A，B两点，该圆上点P，使得⊿PAB面积等于3，这样的点P共有 （ ）
(A) 1个 (B) 2个 (C) 3个 (D) 4个
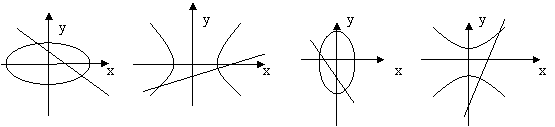
5．设a，b∈R，ab≠0，那么直线ax－y＋b＝0和曲线bx2＋ay2＝ab的图形是
A
B
C
D
6．过抛物线y2＝8(x＋2)的焦点F作倾斜角为60o的直线，若此直线与抛物线交于A、B两点，弦AB的中垂线与x轴交于P点，则线段PF的长等于 （ ）
A． 
B． 
C．
D．
7．方程
表示的曲线是
( )
A. 焦点在x轴上的椭圆 B. 焦点在x轴上的双曲线
C. 焦点在y轴上的椭圆 D. 焦点在y轴上的双曲线
8、教室内有一直尺，无论怎样放置，在地面总有直线与直尺所在直线 ( )
A、平行 B、垂直 C、相交 D、 异面
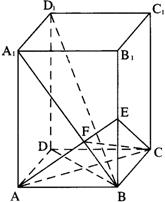
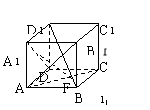9．如图，正方体ABCD-A
BCD中，EF是异面直线AC和AD的公垂线，则EF和BD关系是
（ ）
A．相交不垂直 B．相交垂直
C．异面直线 D．互相平行
10．有一正方提纸盒展开如图，在原正方体纸盒中有如下结论：①AB⊥EF②AB和CM成60°③EF和MN为异面直线④MN∥CD，其中正确序号是
（ ）
A．①②
B．③④
C．②③
D．①③
二、填空题（每题5分共20分）
11．在椭圆
中，记左焦点为F，右顶点为A，短轴上方的端点为B。若该椭圆的离心率是
，则
=
。
12．设F1，F2是椭圆
的两个焦点，P是椭圆上的点，且PF1 : PF2＝2 : 1，则三角形
PF
13．若正方形ABCD的一条边在直线
上，另外两个顶点在抛物线
上.则该正方形面积的最小值为 .
14．对于四面体ABCD，给出下列四个命题：①若AB=AC，BD=CD则BC⊥AD；②若AB=CD，AC=BD则BC⊥AD；③若AB⊥AC，BD⊥CD则BC⊥AD；④若AB⊥CD， BD⊥AC则BC⊥AD；其中真命题序号是 ．
三、解答题（15，16题各10分，17，18题各12分，19，20题各14分）
15．求过原点且与直线x=1 及圆(x-1)2+(y-2)2=1均相切的圆的方程。
16．把椭圆
绕它的中心旋转90°，再沿x轴方向平行移动，使变换后的椭圆截直线
所得线段长为，求变换后的椭圆方程。
17．设曲线C1:
(a为正常数)与C2:y2=2(x+m)在x轴上方公有一个公共点P。
（1）实数m的取值范围（用a表示）；
（2）O为原点，若C1与x轴的负半轴交于点A，当0<a<
时，试求⊿OAP的面积的最大值（用a表示）。
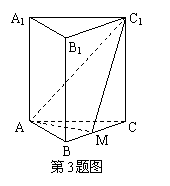
18．如图，已知正四棱柱ABCD—A1B
|
|
（Ⅰ）求证：D1B⊥平面AEC；
（Ⅱ）求三棱锥B—AEC的体积；
（Ⅲ）求二面角B—AE—C的大小.
19．在平面直角坐标系xoy中，给定三点
，点P到直线BC的距离是该点到直线AB，AC距离的等比中项。
（Ⅰ）求点P的轨迹方程；
（Ⅱ）若直线L经过的内心（设为D），且与P点的轨迹恰好有3个公共点，求L的斜率k的取值范围。
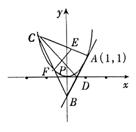
20．过抛物线上的一点A（1,1）作抛物线的切线，分别交
轴于D，交
轴于B.点C在抛物线上，点E在线段AC上，满足
;点F在线段BC上，满足
，且
，线段CD与EF交于点P.当点C在抛物线上移动时，求点P的轨迹方程.
2005~2006年皖南十校期末联考
1.C 2.B 3.B 4.B 5.B 6.A 7.C 8.B 9.D.10.D
11.90º
12.设椭圆的长轴、短轴的长及焦矩分别为
，故，PF1＋PF2＝，而22＋42＝(2)2，可见△PFlF2是直角三角形，且两直角边的长为2和4，故△PFlF2的面积＝4．
13.解：设正方形的边AB在直线上，而位于抛物线上的两个顶点坐标为
、
，则CD所在直线
的方程
将直线的方程与抛物线方程联立，得
令正方形边长为
则
①
在上任取一点（6，,5），它到直线
的距离为
②.
①、②联立解得
或
14.1,3
15．
16.
或
17. 解：(1)由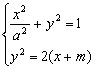
消去y得：
①
设
，问题(1)化为方程①在x∈(－a，a)上有唯一解或等根．
只需讨论以下三种情况：
1°△＝0得：
，此时xp＝－a2，当且仅当－a＜－a2＜a，即0＜a＜1时适合；
f (a)＝0得m＝－a，此时xp＝－a－
综上可知，当0＜a＜1时，或－a＜m≤a；
当a≥1时，－a＜m＜a．
(2)△OAP的面积
∵0＜a＜
，故－a＜m≤a时，0＜
＜a，
由唯一性得 
显然当m＝a时，xp取值最小．由于xp＞0，从而yp＝
取值最大，此时
，∴
．
当时，xp＝－a2，yp＝
，此时
．
下面比较
与
的大小：
令
，得
故当0＜a≤
时，≤，此时
．
当
时，
，此时
．
18.证（Ⅰ）∵ABCD—A1B
∴D1D⊥ABCD.
连AC，又底面ABCD是正方形，
∴AC⊥BD，
由三垂线定理知 D1B⊥AC.
同理，D1B⊥AE，AE∩AC = A，
∴D1B⊥平面AEC .
解（Ⅱ）VB－AEC = VE－ABC .
∵EB⊥平面ABC，
∴EB的长为E点到平面ABC的距离.
∵Rt△ABE ~ Rt△A1AB，
∴EB
=
∴VB－AEC = VE－ABC =
S△ABC·EB
|
|
=×
×3×3×
=
（10分）
解（Ⅲ）连CF，
∵CB⊥平面A1B1BA，又BF⊥AE，
由三垂线定理知，CF⊥AE .
于是，∠BFC为二面角B—AE—C的平面角，
在Rt△ABE中，BF =
，
在Rt△CBF中，tg∠BFC =
，
∴∠BFC
= arctg
.
即二面角B—AE—C的大小为arctg.
19. 解：（Ⅰ）直线AB、AC、BC的方程依次为
。点
到AB、AC、BC的距离依次为
。依设，
，即
，化简得点P的轨迹方程为
圆S：
（Ⅱ）由前知，点P的轨迹包含两部分
圆S：
①
与双曲线T：
②
因为B（－1，0）和C（1，0）是适合题设条件的点，所以点B和点C在点P的轨迹上，且点P的轨迹曲线S与T的公共点只有B、C两点。
的内心D也是适合题设条件的点，由
，解得
，且知它在圆S上。直线L经过D，且与点P的轨迹有3个公共点，所以，L的斜率存在，设L的方程为
③
（i）当k=0时，L与圆S相切，有唯一的公共点D；此时，直线
平行于x轴，表明L与双曲线有不同于D的两个公共点，所以L恰好与点P的轨迹有3个公共点。......10分
（ii）当
时，L与圆S有两个不同的交点。这时，L与点P的轨迹恰有3个公共点只能有两种情况：
情况1：直线L经过点B或点C，此时L的斜率
，直线L的方程为
。代入方程②得
，解得
。表明直线BD与曲线T有2个交点B、E；直线CD与曲线T有2个交点C、F。
故当时，L恰好与点P的轨迹有3个公共点。
情况2：直线L不经过点B和C（即
），因为L与S有两个不同的交点，所以L与双曲线T有且只有一个公共点。即方程组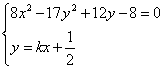
有且只有一组实数解，消去y并化简得
该方程有唯一实数解的充要条件是
④
或
⑤
解方程④得
，解方程⑤得
。
综合得直线L的斜率k的取值范围是有限集
。 .
20.解一：过抛物线上点A的切线斜率为：
切线AB的方程为
的坐标为
是线段AB的中点.
设、
、
、
，则由知，
得
∴EF所在直线方程为：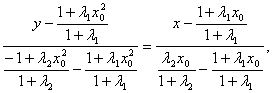
化简得
当
时，直线CD的方程为：
…②
联立①、②解得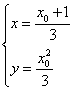
，消去
，得P点轨迹方程为：
当
时，EF方程为：
方程为：
，联立解得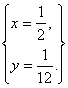
也在P点轨迹上.因C与A不能重合，∴
∴所求轨迹方程为
解二：由解一知，AB的方程为
故D是AB的中点.
令
则
因为CD为的中线，
而
是的重心.
设
因点C异于A，则
故重心P的坐标为
消去
得
故所求轨迹方程为