44.复数的三角形式
一、典型例题
1.
设z1=![]() +i,z2=1-i,z3=sin
+i,z2=1-i,z3=sin![]() +icos
+icos![]() ,求
,求![]() 的值。
的值。
2.
已知复数z的模等于1,辐角q∈![]() ,设u=z3+
,设u=z3+![]() ,①求u的取值范围;②当q≠
,①求u的取值范围;②当q≠![]() 时,求argu的取值范围。
时,求argu的取值范围。
3.
①已知z1=cosa+isina,z2=cosb+isinb且z1+z2=![]() ,求z1·z2的值;
,求z1·z2的值;
②求使![]() 成立的最小正整数n。
成立的最小正整数n。
4. 当实数x为何值时,z=(1+cosx+isinx)5是实数?
5.
已知数列{zn}是首项为24,公比为![]() 的等比数列,如果将这个数列的实数项不改变原来的前后次序,从首项起排成一个实数数列,①写出这个实数数列的前4项;②求这个实数数列的前10项的和。
的等比数列,如果将这个数列的实数项不改变原来的前后次序,从首项起排成一个实数数列,①写出这个实数数列的前4项;②求这个实数数列的前10项的和。
6.
在⊿ABC中,c2>a2+b2,z1=1+cos2A+isin2A,z2=1+cos2B+isin2B,z3=1+cos2C-isin2C,求证:![]() 是正实数。
是正实数。
7. 把下列复数化为三角形式:
①-3+![]() i; ②3-4i; ③-3(sin
i; ②3-4i; ③-3(sin![]() -icos
-icos![]() ); ④1-cosq-isinq(0<q<2p)
); ④1-cosq-isinq(0<q<2p)
8. 求下列复数的辐角主值和模:
① sin50°-icos50°; ② -5-12i; ③ 1+cos220°+isin220°
9.
若复数z=(2k2-3k-2)+(3k2+k-2)i的辐角主值是![]() ,求实数k。
,求实数k。
10.
设z∈C,arg(z+1)=![]() ,arg(z-1)=
,arg(z-1)=![]() ,求复数z。
,求复数z。
11.
已知arg(3+4i)=q1,arg(![]() )=q2,求q1+q2。
)=q2,求q1+q2。
12.
化简![]() 。
。
13. ①求7-24i的四次方根;②在复数集内分解因式:x6-1。
14.
求最小的自然数n,使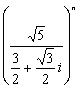 >0
>0
15. 已知z=1,且z5+z-1=0,求复数z。