高二数学竞赛团体赛

高中二年级　　班 学号　　  姓名　　　　　  　成绩　　　　　　　

　一．选择题：

　1．已知6<a<10, ≤b<2a, 且c=a＋b, 那么（　）。

　（A）15≤c<30　（B）9<c≤18　（C）9≤c<18　（D）9<c<30

　2．函数y=5arccosx的反函数一定是（　）。

　（A）y=5cos, x∈[0, 5π]　（B）y=cos, x∈[0, 5]

　（C）y=cos, x∈[0, π]　 （D）y=5cosx, x∈[0, π]

　3．设x∈R,且0<x－5＋x－3<m, 则m的取值范围是（　）。

　（A）m>1　　（B）m≥1　　（C）m>2　　（D）m≥2

　4．直线y=2x＋1被圆x²＋y²－2y－1=0所截得的线段的长是（　）。

　（A）2　　（B）2 　 （C）　　（D）1

　5．设实数a, b, c满足a＋b＋c=0且abc≠0, 则必有（　）成立。

　（A）abc>0　　　　  （B）(a＋b＋c)≥

　（C）a³＋b³＋c³>abc  （D）ab＋bc＋ca<0

　6．已知在平面直角坐标系内，点A(a＋2, b＋2)与点B(b－4, a－6)共有直线4x＋3y=11对称，那么（　）。

　（A）a=－4, b=2　（B）a=4, b=－2　（C）a=4, b=2　（D）a=2, b=4

　7．如果实数a, b同时满足以下两个不等式：0<ab<1, 0<a＋b<1＋a²b², 那么必有（　）。

　（A）　　　　  （B）且a<1或者且b<1

　（C）0<a<1且0<b<1　（D）以上都不对

　8．点集合{(x, y) lg(x³＋y³＋)=lgx＋lgy}中, 元素的个数为（　）。

　（A）0个　（B）1个　（C）2个　（D）多于2个

　二．填空题：

　 9．已知x₁, x₂是方程x²－(k－2)x＋(k²＋3k＋5)=0 (k∈R)的两个实数根，那么x₁²＋x₂²的最大值为　　　　　　　　　  。

　10．两条直线2x²－5xy＋y²=0的夹角为　　　　　　　　　 。

　11．已知椭圆的中心在原点，其一个焦点为F₁(3, 0)且点P(4, 2.4)在椭圆上，那么点P到F₁相应的的准线的距离是 　　　　　　　　　。

　12．已知A(4, －4)是双曲线上一点，其中<α<π, 那么这个双曲线的焦点坐标是　　　　　　　　　　  。

　13．不等式log< log(8－x)的解集是　　　　　　　　　　  。

　14．方程x²＋y²=x＋y在平面直角坐标系中所围成的图形的面积是　　　　　　　　  。

　三．解答题：

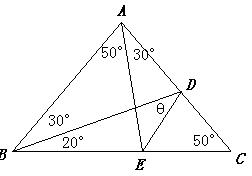
　15．如图，D、E分别是△ABC的AC及BC边上的点，且∠ACB＝∠BAE＝50°，∠DBC＝20°，∠ABD＝∠CAE＝30°，∠BDE＝θ，试求θ的度数。

　16．设a, b是互不相等的正数，且A=, B=, 试证：B<<A.

　17．对于每个自然数n，试球出最大的正整数k，使得在含有n个元素的集合中，可以找出k个子集，而其中任意两个子集的交集非空。

　18．设x, y, z>0, 且x²＋y²＋z²=1, 试求S=的最小值。

　19．设对于每一个θ的值，方程2(2sinθ－cosθ＋3)x²－(8sinθ＋cosθ＋1)y=0表示一条曲线，求这些曲线中，在直线y=2x上所截得的线段长的最大值。

参考答案

题号	1	2	3	4	5	6	7	8
答案	D	B	C	B	D	C	C	B

 9．18　　　　　　　　　　　 10．arctg

11．　　　　　　　　　　  12．(0, ±2)

13．{x <x<2或7<x<8}　　　14．π＋2

15．解： ∠ABE=∠EAB, AE=BE,

　在△BDE中，

　sinθ=,

　在△AED中， ==2sin(7＋θ),

　∴ sinθ=2sin2sin(7＋θ)=－cos(9＋θ)＋cos(5＋θ),

　∴cos(5＋θ)=0, ∴5＋θ=9, θ=4.

16．证明：(a－b)²=4[()²－()²]=4(A²－B²),

　∵ a, b是不相等的正数，∴ A－B=－=(－)²>0,

　∴ A>B,　 ∴=,

　又∵ B－=<0, A－=>0, ∴ B<<A,

　即B<<A .

17．解：设找出的k个子集为A₁、A₂、……、A_k, 原来含有n个元素的集合为I，

　则A_iI, A_i∩A_j≠, (i≠j, 1≤i, j≤k)

　考虑这k个子集的补集，且A_i≠, A_i≠A_j,,

　假设对于i≠j, 1≤i, j≤k, 有A_i=, 那么A_i∩A_j=∩A_j=, 矛盾,

　∴A_i≠, 即这2k个子集互不相等，而含有n个元素的集合上有2ⁿ个子集，

　∴ 2k≤2ⁿ, k≤2^k－1.

18．解：　S²=()²=+2(x²+y²+z²),

　2()≥2(x²+y²+z²)=2,

　∴ S²≥3, S≥, ∴ S的最小值为

19．解：联立方程，将y=2x代入2(2sinθ－cosθ＋3)x²－(8sinθ＋cosθ＋1)y=0得

　2(2sinθ－cosθ＋3)x²－2(8sinθ＋cosθ＋1)x=0, 解得x₁=0, x₂=,

　截得的线段的长l=x₁－x₂,

　x₁－x₂=, 设z=,

　则(2z－8)sinθ－(z＋1)cosθ=1－3z, 即sin(θ＋φ)=1－3z,

　∵ sin(θ＋φ)≤1, ∴ (1－3z)²≤(2z－8)²＋(z＋1)², 整理得z²＋6z－16≤0,

　∴ －2≤z≤8, ∴x₁－x₂≤8, 弦长l的最大值是8.