高二期末数学复习试卷
一、选择题(![]() )
)
1、已知α、β是两个不重合的平面,l、m是两条不重合的直线,则α∥β的一个充分条件是………………………………………( )
(A)
![]() (B)
(B)
![]()
(C)
![]() (D)
(D)
![]()
2、在正方体ABCD-A1B1C1D1过顶点A1在空间作直线![]() ,使
,使![]() 与直线AC、BC1所成的角都等于60°,这样的直线的条数为………( )
与直线AC、BC1所成的角都等于60°,这样的直线的条数为………( )
(A) 1 (B) 2 (C) 3 (D) 4
3、已知菱形ABCD的边长为1,∠DAB=60°,将这个菱形沿AC折成120°的二面角,则B,D两点间的距离为………………………( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
4、PA、PB、PC为三条射线,且 ∠APB = ∠APC= 60°, ∠BPC=90°,则PA与平面BPC所成的角为…………………( )
(A)30° (B)45° (C)60° (D)90°
5、6人并排站成一排,乙必须站在甲的右方,丙必须站在乙的右方,则不同排法的种数为……………………………………………( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
6、用1,2,3,4,5,7这6 个数字排成无重复的六位数,其中偶数数字不相邻的排法有………………………………………………………( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
7、在100件产品中,有3件是次品,现从中任意抽取5件,其中至少有2件次品的取法种数为………………………………………( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
8、n是奇数,二项式(1-x)2n+1展开式中系数最大的项是…( )
(A)第n项(B)第n+1项(C)第n+2项(D)第n+1,n+2项
9、二项式![]() 的展开式中,有理项共有………( )
的展开式中,有理项共有………( )
(A)3项 (B)5项 (C)6项 (D)7项
10、从装有白球3个、红球4个的箱子中,把球一个一个地取出来,到第五个恰好把白球全部取出的概率是………………………( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
11、从两件正品和两件次品中任取两件互为对立事件的是( )
(A)至少有一件正品与至少有一件次品
(B)恰有一件正品与恰有两件正品
(C)至多有一件次品与全是次品
(D)至少有一件正品与全是正品
12、一次游戏中有人出了12道选择题,每题附有4个答案,其中只有一个是符合要求的。有人每做一道题都对1,2,3,4四数字抽签,抽到几就把第几个答案填上去,则恰好做对4题的概率为………………( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
二、填充题(![]() )
)
13、正四面体相对两棱所成的角为 .
14、坐标平面上有点A(-2,3)和B(4,-1),将坐标平面沿y轴折成二面角,使A,B两点的距离为![]() ,则该二面角等于 .
,则该二面角等于 .
15、0.99810精确到0.001的近似值为 .
16、有5件不同的玩具全部分给3个儿童,每人至少一件,不同分法有 种.
17、有6门大炮对同一目标进行射击,若目标被击中的概率不小于0.90,每门大炮击中目标的概率p相同,则p的最小值为 .
18、有4台设备,每台正常工作的概率均为0.9,则4台中至少有3台能正常工作的概率为 .
三、解答题
19、(排列组合)(8)
30030能被多少个不同的偶数整除?
20、(立几)(8)
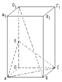
如图,在正四棱柱ABCD-A1B1C1D1中,点E在棱DD1上,截面EAC//D1B,且平面EAC与底面ABCD所成的角为45°,AB=a.
(1)求截面EAC的面积;(2)求异面直线A1B1与AC之间的距离.
21、(二项式定理)(8)
设m,n是正整数,f(x)=(1+x)m+(1+x)n,已知f(x)展开式中,x的系数为19.
(1)当m,n为何值时,x2的系数最小;
(2)当x2的系数最小时,求x7的系数。
22、排列组合(10)
从5个男生和3个女生中选5人担任5门不同学科的课代表,求符合下列条件的选法数:(1)女生必须少于男生;(2)某女生担任语文课代表;(3)某男生必须包括在内,但不担任数学课代表;(4)某女生必须担任语文课代表,某男生必须担任课代表,但不担任数学课代表.
23、概率(10)
甲乙二人各提一个装有卡片的提包,从中取出卡片来比胜负。甲的提包里有号码为1的卡片2张,号码为3的卡片1张;乙的提包装有号码为1的卡片1张,号码为2的卡片2张。甲、乙同时从自己的提包里每次取出卡片1张相比,取出的不再放回,直到二人取出的卡片号码不相同时,号码大的一方为胜。求甲、乙二人分别获胜的概率。
24、概率(12)
某人忘记了电话号码的最后两个数字,因而他随意拨号.
(1)求第3次接通电话的概率
(2)求拨号不超过3次而接通电话的概率
(3)若最后一个数字是奇数,求拨号不超过3次而接通电话的概率