高二期末考试模拟试题(数学) 2003.1.2
一、选择题(共12小题,每小题5分,共60分)
1、直线l的倾斜角为![]() ,且
,且![]() ,则直线l的斜率是
,则直线l的斜率是
A. ![]() B.
B.![]() C.
C.![]() 或
或![]() D.
D. ![]() 或
或![]()
2、已知直线![]() ,其中a、b、c同号,则直线与两坐标轴围成的三角形的面积是
,其中a、b、c同号,则直线与两坐标轴围成的三角形的面积是
A. ![]() B.
B.![]() C.
C. ![]() D.
D.
![]()
3、已知空间四边形ABCD,连AC、BD,设M和G分别是BC、CD的中点,则AB+![]() =
=
A. ![]() B. CG
C. BC
D.
B. CG
C. BC
D.![]()
4、正方体ABCD—A1B1C1D1中,E、F分别是BB1、CC1的中点,则AE、BF所成的角的余弦值是
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.![]()
5、空间四边形OABC中,OB=OC,![]() ,则
,则![]()
A. ![]() B.
B.
![]() C.
C.![]() D.0
D.0
6、设A![]() ,B
,B![]() ,C
,C![]() ,则
,则![]() 的形状是
的形状是
A.等腰三角形 B.等边三角形 C.直角三角形 D.等腰直角三角形
7、若![]() 且
且![]() ,则
,则![]() 的最大值是
的最大值是
A.
8
B. 10
C. ![]() D.
D.
![]()
8、设x、y满足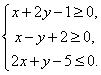 则
则![]() 的最大值是
的最大值是
A. 4 B. 3 C. 2 D. 1
9、如果直线l、m与平面α、β、γ满足:![]() ,
,![]() ,
,![]() ,那么必有
,那么必有
A.![]() B.
B. ![]() C.
C.![]() D.
D.![]()
10、平面上动点P到定点F(1,0)的距离比P到y轴的距离大1,则动点P的轨迹方程为
A.![]() B.
B.![]() C.
C. ![]() 或
或![]() D.
D. ![]() 或
或![]()
11、曲线![]() 与直线
与直线![]() 有两个交点,则实数
有两个交点,则实数![]() 的取值范围是
的取值范围是
A. ![]() B.
B.![]() C.
C.![]() D.
D.![]()
12、![]() 是椭圆短轴的两端点,过左焦点
是椭圆短轴的两端点,过左焦点![]() 作长轴的垂线,交椭圆于P,若
作长轴的垂线,交椭圆于P,若![]() 是O
是O![]() 和
和![]() 的比例中项(O为椭圆中心),则
的比例中项(O为椭圆中心),则![]() 的值为
的值为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
请把选择题答案填入下表:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
班级 姓名 学号 分数
二、填空题(共4小题,每小题4分,满分16分).将正确答案直接填在横线上.
13.在正方体![]() -
-![]() 中,
中,![]() 与平面
与平面![]() 所成角的大小为
.
所成角的大小为
.
14.设双曲线![]() 的右准线与两条渐近线交于A、B两点,右焦点为
的右准线与两条渐近线交于A、B两点,右焦点为![]() 且
且![]() 则双曲线的离心率为
.
则双曲线的离心率为
.
15.已知向量![]() ,
,![]() ,若
,若![]() 与
与![]() 成
成![]() 角,则k= .
角,则k= .
16.过点![]() 作直线l与抛物线
作直线l与抛物线![]() 仅有一个公共点的直线方程是
.
仅有一个公共点的直线方程是
.
三、 解答题(共6小题,满分74分)
17、已知向量
![]() ,求(1)
,求(1)![]() ;(2)∣a∣、∣b∣;(3)
;(2)∣a∣、∣b∣;(3)![]() 。
。
18、在棱长为a的正方体ABCD—A1B1C1D1中,设M、N、E、F分别是棱A1B1、A1D1、C1D1、B1C1的中点.
(1) 求证:E、F、B、D四点共面;
(2) 求证:平面AMN // 平面EFBD。
|
|
|
|
|
|
|
|
|
|
|
|

19、在棱长为a的正方体ABCD—A1B1C1D1中E、F分别是AB、BC的中点,EF交BD于N。问:棱BB1上是否存在点M,使D1M⊥平面B1EF,并说明理由;若存在,试求A1N与D1M所成角。
|
|
|
|
|
|
|
|
|
|

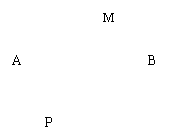
20、某工程要挖一个横断面为半圆的柱形的坑,挖出的土只能沿道路AP,BP运到P处(如图所示)。![]()
![]() ,试说明怎样运土才能最省工?
,试说明怎样运土才能最省工?

21、已知圆C过定点A(0,a)(a>0),且在x轴上截得的弦MN的长为2a。
(1) 求圆C的圆心的轨迹方程;
(2)
设![]() ,求
,求![]() 的最大值,及此时圆C的方程。
的最大值,及此时圆C的方程。
22、点A(x1 ,y1),B(x2 ,y2)是曲线![]() 上两点,且OA⊥OB(O为坐标原点)。
上两点,且OA⊥OB(O为坐标原点)。
(1) 求证:y1 y2是定值;
(2) 求证:直线AB经过一个定点;
(3) 求原点O在直线AB上的射影M的轨迹。