高二年级第一学期期中考试数学试题（1）

高二年级第一学期期中考试数学试题

一．选择题（每题3分,共45分.请把答案填在本题后的相应的表格内）

1.若a>b且c<0则有（　　）

A.ac>bc　 B. ac<bc　 C. ac＝bc　 D. ac与bc的大小不能确定

2.若a>b 那么(　　)

A.2c-a>2c-b　 B.2a-c<2b-c　 C. 2a+c>2b+c　 D.2c+a<2c+b

3.圆C：=0的圆心和半径分别为（　　）

A.(, ), 1　 B.(2, ,　C.(1, ),　D.(1, ),

4．斜率为3，在x轴上的截距为4的直线方程是（　 ）

　A. y=3x+4　　B. x=3y+12　　C. 3x=y　　D. 3x=y+12

5.满足不等式组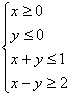的可行域内使目标函数ｚ=取得最大值的点的坐标是(　　)

　A .  (0, 0)　　B. ()　 C. (0，)　 D. (1，0)

6.已知a<0,　<b<0那么(　　)

A. a>ab>ab²　 B. ab²>ab>a　 C. ab>a>ab²　 D. ab>ab²>a

7.直线的斜率为,则其倾斜角为(　　)

　A.π+arctan3　B. arctan()　C. –arctan()　D.π+arctan()

8.直线l₁: 和 l₂: y=+1关系为(　　)

　A.平行　　 B. 垂直　　 C. 相交但不垂直　　 D. 重合

9.不等式：的解集是(　　　)

　Ａ. 　B.（ 0）　C. 　 D.

10.直线有斜率是直线有倾斜角的(　 )

A.　 充分不必要条件　　　 B. 必要不充分条件

C. 充要条件　　　　　　 D.即不充分又不必要条件

11.直线l_1: x+3y=1直线l₂的斜率为, 则l₂到l₁的角为(　 )

　A.  45⁰　　 B.　120⁰　　 C .　135⁰　　　D. 150⁰

12.直线2x-3y+2=0和曲线y=的交点到直线y=1-的距离是(　)

　A. 　　　B. 　　　C. 　　　D.

13.已知: x<0, 则  有(　 )

A. 最大值-2　 B. 最小值2　 C. 最小值-2　 D. 最大值2

14.a,b是不等的实数,则下列不等式总成立的是(　 )

　A.>2　  B.　 C.　 D.

15.两直线a, b互不垂直,a到b的角为,　a, b的夹角为β, 则下列不等式中不一定成立的是(　 )

A.sin=　B.=cosβ C. tan=　D. =cotβ

请把选择题的答案填在此表格内

题号	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
答案

第Ⅱ卷（非选择题共55分）

二.填空(每小题3分,共15分)

16.由两点A(1, 2), B(, 4) 所确定的直线的斜率为　　　　　　  ．

17.已知5<x<7, <y<3, 则x的取值范围是　　　　　　　　  ．

18.不论m为何实数,方程 (3m+4)x+(5-2m)y+7m=0 所表示的直线总过一定点,则该点的坐标为　　　　  ．

19.不等式  的解集为　　　　　　　　　 ．

20. 已知点 A (3,),B (, 4), 则以线段AB为直径的圆的标准方程

为　　　　　　　　　　　．

三.解答题(共40分)

21.已知  都是正数，且 , 求证: 　(7分)

22.设0<x<2, 求函数y=的最大值,并写出此时x的值.(7分)

 

 

23.动点P到直线l: y=的距离等于它到点A (0,4) 的距离,求动点P的轨迹方程． (只求方程不用证明)　(8分)

24.求直线a: 2x-y+3=0 关于直线l: x+y+1=0 的对称直线b的方程,并化为截距式． (8分)

25.解不等式　，其中0<a<2．　 (10分)