复数专题训练（四）
班级 ________ 姓名__________ 记分___________
28、（本小题满分12分）(续前)
复数z1、z2满足z1=z2=1，z1、z2在复平面内的对应点分别为Z1、Z2，O为原点．
（1）
若z2-z1=-1，求arg
； (2) 设argz1=α，argz2=β，若ΔOZ1Z2的重心对应复数
+
i，求tg(α+β)的值．
29、（本小题满分12分）
设z为复数，D为满足条件z-1+z-1=0的点Z所构成图形的边界．
（1）
若复数ω=
z+1-2i(z∈D)，求ω对应点的轨迹方程；
（2）
若满足条件z+=z-
i所构成的图形D/与D有两个公共点A、B，OA、OB的倾斜角分别为α、β（O为原点），求cos(α+β)的值．
30、（本小题满分14分）
设无穷数列{zn}满足z1=-1+i，zn在复平面上的对应点为Zn(n=1，2，…)，将向量
沿逆时针方向旋转
，且使模扩大到原来的
倍就得到向量
． (1). 求这个数列的通项公式； (2). 已知数列的第n项为-32，求n； (3) .将数列{zn}中的实数项的倒数按原顺序排成一个新数列{bn}，并设Sn=b1+b2+…+bn，求
Sn．
参考答案： DCCBA AADCC BDBDD
16、10, 0翰林汇
17、{-2,0,2}翰林汇
18、8
，
翰林汇
19、(1)Z为实数(2)0或1或-
翰林汇
20、
;翰林汇
21、
;翰林汇翰林汇
22、(1) –1; (2) 300o; (3) -2I; (4)__________
23、以( －1 , 0 ) 为圆心, 2为半径的圆 .
24、解析：设Z1=cos
＋isin,Z2=-4(cos
＋isin)
∵Z1－Z2=1－2
,∴
(1)2＋(2)2得
1＋16－8cos(－)=13,∴cos(－)=,sin(－)=
∴
=
=[cos(－)＋isin(－)]=
i
25、．解：由z1=1，则
=
，z2=4，则
=
，∴z1-z22=z12+z22-z2-z1=1-2
i2=13，∴z2+z1=4，即+16
=4，∴16（）2-4+1=0，∴=
，ω=
=
（1±i）-3=-
±
i．
26、解：（1）设x0为原方程一实根，则x02-2(1+i)x0+ab-(a-b)i=0，所以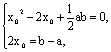
消去x0得(a+2)2+(b-2)2=8，所以-2-2≤a≤2-2，2-2≤b≤2+2．
（2）设a+2=2cosθ，b-2=2sinθ，则x0=
=2sin(θ-)+2∈[0，4]，所以此方程实根的最大值为4，最小值为0．
27、解：设z的辐角主值为θ，则2z、3z的辐角的主值均为θ．∵z=2，∴2z=4，3z=6，∴S
=OA·OP3·sinθ=3sinθ，S
=OA·OP1·sinθ=sinθ，∴S
+S
= S- S=2sinθ=2，∴sinθ=1，即θ=
或θ=
，故z=2i或z=-2i．
28、．解：（1）因为z1=z2=1，所以
=1，设=cosθ+isinθ，θ=arg，代入z2-z1=-1，得(cosθ+isinθ)z1-z1=-1，所以z1(cosθ+isinθ-1)=-1，所以(cosθ-1)+isinθ=1，即
=1，
=1，cosθ=，所以arg=θ=
或
．
（2）设z1=cosα+isinα，z2=cosβ+isinβ，则
=，且
=，即
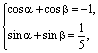解得tg
=
，所以tg(α+β)=
．
29、解：由已知，曲线D为z=1．
（1） 由ω=z+1-2i得：ω-1+2i=z=，所求轨迹方程为(x-1)2+(y+2)2=
．
（2） 由z+=z-i及z=1，得（z+）（
+）=（z-i）(+i)，且z=1，
化简得(3i-1)z2+4z-1-3i=0，所以zA·zB=-
=-
+
i，又由于zA=cosα+isinα，zB=cosβ+isinβ，所以zA·zB=cos(α+β)+isin(α+β)，所以cos(α+β)=-．
30、解：（1）由题设知zn+1=(cos+isin)zn=(1+i)zn，所以zn是以-1+i为首项，公比为1+i的等比数列，所以zn=(-1+i)(1+i)n-1=i(1+i)n．
（2）因为zn= i(1+i)n=i()n=(cos
+isin)，要zn∈R，则cos=0， =kπ+，n=4k+2(k=0，1，2，…)，所以{zn}的实数项为z2，z6，z10，…，z4k+2，…，所以
=-，所以{bn}是首项为-，公比q=-的等比数列，所以Sn=
=-
．